|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Физики оценили время падения к центру Земли |
Физики оценили время падения к центру Земли
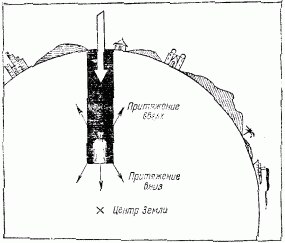
Колодец, пронзающий Землю насквозь — классический виртуальный объект, на примере которого можно изучить одновременно закон всемирного тяготения и гармонические колебания. Задача о падении тела в колодце, который проходит через центр Земли, хорошо известна и легко решается, если сделать ряд предположений. Во-первых, будем считать, что масса Земли распределена равномерно, во-вторых, что в колодце нет воздуха. Тогда, составив второй закон Ньютона, мы увидим, что оно похоже на уравнение гармонического осциллятора, иными словами — маятника.
Подставив все величины окажется, что период колебаний тела, падающего через центр Земли равен 84 минутам, а значит путь из одной точки земного шара в противоположную ей займет всего 42 минуты, если успеть выбраться из колодца.
Если учесть современные знания о строении Земли, то в это уравнение стоит добавить колебания плотности нашей планеты в зависимости от расстояния от центра. Это проделал в 2015 году канадский аспирант Александр Клотц. Статья с подробностями расчета была опубликована в журнале American Journal of Physics. При расчете времени падения, а также закона движения тела считают, что Земля в каждой своей точке обладает одинаковой плотностью — около 5,5 тонн на кубометр. Тогда оказывается, что положение тела в разные моменты времени меняется по законам синуса или косинуса (по такому же закону, например, меняется отклонение маятника от вертикали) — это и есть пример гармонических колебаний. Время падения оказывается равным 42 минутам.
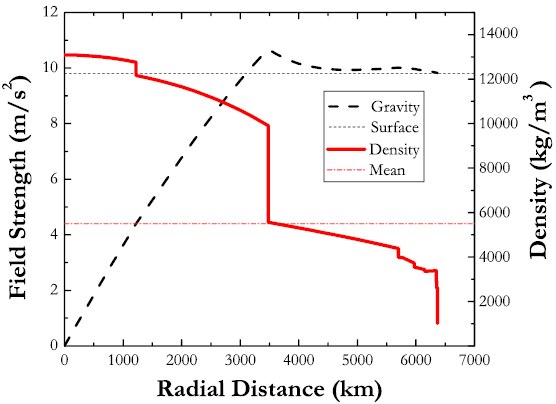
Однако плотность Земли не является величиной постоянной. Александр Клотц захотел решить эту задачу более точно и взял распределение плотности по одной из принятых на сегодня моделей строения Земли — от тонны на кубометр на поверхности до 13 тонн на кубометр в центре Земли, с резким изменением на границе внешнего ядра (около 3500 километров от центра). Оказалось, что суммарное время падения должно составить 38 минут 11 секунд вместо 42 минут 12 секунд. Любопытно, что практически такой же результат можно получить, просто считая значение силы тяжести не меняющимся при движении вглубь планеты. Тогда плотность Земли принимается бесконечно увеличивающейся по мере приближения к центру. В реальности плотность ядра практически постоянна в разных его точках, но в пределах ядра тело проводит столь мало времени, что разница между очень грубой моделью и реальностью просто не успевает оказать воздействие на результат. В 2016 году физики из Кинг колледжа (Пенсильвания) уточнили время падения объекта в колодце, проходящем через центр Земли. Для того, чтобы сделать оценку более реалистичной авторы новой работы сделали следующий шаг и учли влияние сопротивления воздуха в колодце или возможного трения о его стенки. Обновленная оценка показывает, что падение к центру Земли займет по меньшей мере 1,8 года. Расчеты опубликованы на сервере препринтов arXiv.org. Атмосферный столб в колодце в можно описать с помощью барометрической формулы. Она предсказывает, что давление при приближении к центру Земли растет экспоненциально. К примеру, согласно ей на глубине 5,8 километров под землей давление достигает двух атмосфер. Это предсказание можно проиллюстрировать замерами давлений в одной из африканских шахт: при глубине в 3,8 километра, давление там достигает 1,6 атмосферы.
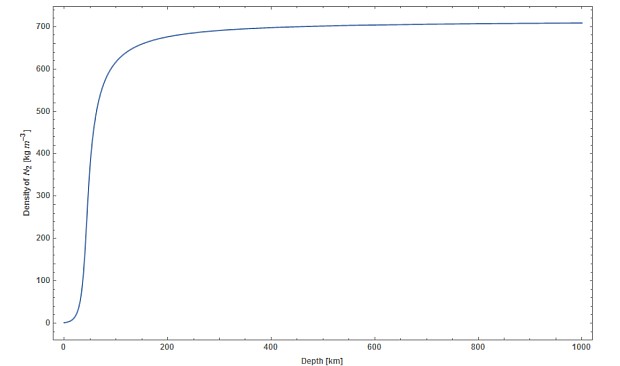
При 58 километрах глубины давление должно уже превышать 1000 атмосфер — газ при этом перестает вести себя как идеальный. Поэтому авторы использовали модифицированную барометрическую формулу, описывающее сжатие газа при высоких давлениях. Однако, даже она дает плотность газа (ученые рассматривали для простоты чистый азот) сопоставимою с плотностью воды — около 650 килограмм на кубометр при глубине 175 километров. Такая плотная среда сильно ограничивает скорость падения. По оценке физиков, время падения к центру Земли составит 1,8 года, а вылет с другой стороны колодца невозможен. Получив этот вывод авторы попробовали оценить, может ли транспортировка в вакуумном колодце (например, поезд) быть сопоставима с простым перелетом вдоль большой окружности Земли. Ученые нашли силу трения, при которой использование такого транспорта будет выгоднее меридионального перелета на Airbus A380. Она составляет 0,35 ньютона на каждый килограмм массы груза. Физики заключают, что несмотря на то, что постройка такого колодца невероятно дорога и технически сложна — практически невозможна — скорость передвижения через вакуумированный тоннель на порядки превышает скорость полета на самолете. Поэтому более развитое технически общество будущего может найти преимущества в постройке такого сооружения.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Физики оценили время падения к центру Земли |
|
[time: 11 ms; queries: 7]
3 Мар 2026 18:50:45 GMT+3 |



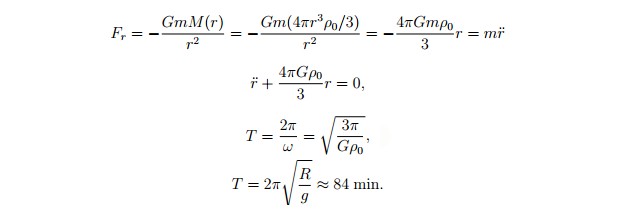
 Вам, наверняка, хоть раз в жизни доводилось стоять у дороги, по которой проносится машина со спецсигналом и включенной сиреной. Пока вой сирены приближается, его тон выше, затем, когда машина поравняется с вами, он понижается, и, наконец, когда машина начинает удаляться, он понижается еще, и получается знакомое: ййййииииээээЭААААОоооуууумммм — такой примерно звукоряд. Сами того, возможно, не сознавая, вы при этом наблюдаете фундаментальнейшее (и полезнейшее) свойство волн.
Вам, наверняка, хоть раз в жизни доводилось стоять у дороги, по которой проносится машина со спецсигналом и включенной сиреной. Пока вой сирены приближается, его тон выше, затем, когда машина поравняется с вами, он понижается, и, наконец, когда машина начинает удаляться, он понижается еще, и получается знакомое: ййййииииээээЭААААОоооуууумммм — такой примерно звукоряд. Сами того, возможно, не сознавая, вы при этом наблюдаете фундаментальнейшее (и полезнейшее) свойство волн.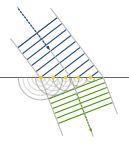 Смысл принципа Гюйгенса проще всего понять, если представить себе, что гребень волны на водной поверхности на мгновение застыл. Теперь представьте, что в этот миг вдоль всего фронта волны в каждую точку гребня брошено по камню, в результате чего каждая точка гребня становится источником новой круговой волны. Практически всюду вновь возбужденные волны взаимно погасятся и не проявятся на водной поверхности. И лишь вдоль фронта исходной волны вторичные маленькие волны взаимно усилятся и образуют новый волновой фронт, параллельный предыдущему и отстоящий от него на некоторое расстояние. Именно по такой схеме, согласно принципу Гюйгенса, и распространяется волна.
Смысл принципа Гюйгенса проще всего понять, если представить себе, что гребень волны на водной поверхности на мгновение застыл. Теперь представьте, что в этот миг вдоль всего фронта волны в каждую точку гребня брошено по камню, в результате чего каждая точка гребня становится источником новой круговой волны. Практически всюду вновь возбужденные волны взаимно погасятся и не проявятся на водной поверхности. И лишь вдоль фронта исходной волны вторичные маленькие волны взаимно усилятся и образуют новый волновой фронт, параллельный предыдущему и отстоящий от него на некоторое расстояние. Именно по такой схеме, согласно принципу Гюйгенса, и распространяется волна. Что заставляет взаимодействовать все в нашей Вселенной? Ускоряются ли тела или замедляются, меняют свое направление или мчатся вперед – почему они ведут себя именно так? Какие законы являются общими и для малейших частиц и для Галактик? С чего все началось, как развивается и как работает? Эти и другие вопросы волновали человека с самых древних времен… Где же ключ к пониманию тайн механической Вселенной? США, 1985 год.
Что заставляет взаимодействовать все в нашей Вселенной? Ускоряются ли тела или замедляются, меняют свое направление или мчатся вперед – почему они ведут себя именно так? Какие законы являются общими и для малейших частиц и для Галактик? С чего все началось, как развивается и как работает? Эти и другие вопросы волновали человека с самых древних времен… Где же ключ к пониманию тайн механической Вселенной? США, 1985 год. Простое двумерное периодическое движение вязкой жидкости может стать хаотическим, что приведёт к эффективному перемешиванию. Эксперименты и компьютерное моделирование проясняют механизм этого явления.
Простое двумерное периодическое движение вязкой жидкости может стать хаотическим, что приведёт к эффективному перемешиванию. Эксперименты и компьютерное моделирование проясняют механизм этого явления. Аристотель и Галилей о падении тел. Силы трения. Скольжение и качение. Статика, кинематика. Векторная природа сил и скоростей. Сложение и разложение. Независимость действий и движений. Сохранение количества движения. Момент силы и момент импульса. Гироскопы. Скамейка Жуковского. Вращательное движение. Момент силы и момент импульса в плоском варианте вращения. Вращение твёрдого тела и момент инерции. Работа, энергия, законы сохранения. Неинерциальные системы и силы. Центробежный эффект. Сила Кориолиса. Задача Эйнштейна о чаинках. Атмосферное давление. Законы Паскаля и Архимеда. Парадокс Архимеда.
Аристотель и Галилей о падении тел. Силы трения. Скольжение и качение. Статика, кинематика. Векторная природа сил и скоростей. Сложение и разложение. Независимость действий и движений. Сохранение количества движения. Момент силы и момент импульса. Гироскопы. Скамейка Жуковского. Вращательное движение. Момент силы и момент импульса в плоском варианте вращения. Вращение твёрдого тела и момент инерции. Работа, энергия, законы сохранения. Неинерциальные системы и силы. Центробежный эффект. Сила Кориолиса. Задача Эйнштейна о чаинках. Атмосферное давление. Законы Паскаля и Архимеда. Парадокс Архимеда.