IV. Данные квантовой механики

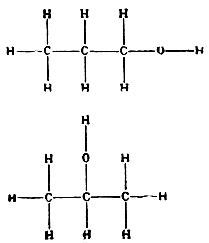
30. Постоянство, не объяснимое классической физикой

Таким образом, при помощи удивительно тонкого инструмента, каким являются рентгеновские лучи (они дали возможность, как помнит физик, 30 лет назад открыть структуру кристаллов), биологам и физикам удалось увидеть более тонкие структуры, ответственные за определенные индивидуальные признаки, то есть удалось определить размер генов более точно, чем методами, описанными в § 17. Мы теперь серьезно стоим перед вопросом: как можно с точки зрения статистической физики примирить то, что генная структура, по-видимому, включает в себя только сравнительно малое число атомов (порядка 1000, а возможно, гораздо меньше) и все же проявляет весьма регулярную и закономерную активность и такое постоянство, какое граничит с чудом.

Разрешите мне пояснить примером это действительно удивительное положение. У нескольких членов габсбургской династии нижняя губа имела особую форму (“габсбургская губа”). Наследование этого признака было изучено очень тщательно, и результаты опубликованы Императорской академией в Вене. Признак оказался настоящим менделевским аллелем по отношению к нормальной губе. Присмотревшись к портретам членов семьи, живших в XVI—XIX столетиях, мы можем уверенно заявить, что материальная генная структура, ответственная за эту ненормальную черту, передавалась из поколения в поколение в течение столетий и в точности воспроизводилась в каждом из немногих клеточных делений, которые происходили в этот период. Более того, число атомов, заключающихся в соответствующей генной структуре, вероятно, должно быть

* И пламенный полет твоего духа довольствуется изображениями и подобиями. — Гете.

51

того же порядка, как и в случаях, проверенных с помощью рентгеновских лучей. Все это время ген находился при температуре около 36° С. Как понять, что он остался неизмененным в течение столетий, несмотря на тенденцию теплового движения к нарушению порядка в структуре?

Физик конца прошлого столетия, основываясь на тех законах природы, которые он тогда мог объяснить и которые он действительно понимал, не нашел бы ответа на этот вопрос. Правда, может быть, после короткого размышления о статистической природе законов, он бы ответил (как мы увидим, правильно) : этими материальными структурами могут быть только молекулы. Химия уже имела в то время достаточное представление о существовании этих ассоциаций атомов и об их иногда очень высокой стабильности.

Но это знание было чисто эмпирическим. Природа молекул не была понята — сильные взаимосвязи атомов, сохраняющие форму молекулы, были для всех полной загадкой. Действительно, ответ оказался бы правильным, но ценность его несколько ограничена, поскольку загадочная биологическая устойчивость сводилась к столь же загадочной химической устойчивости. Любое представление о том, что две особенности, сходные по проявлению, основаны на одном и том же принципе, всегда ненадежно до тех пор, пока неизвестен сам принцип.

31. Объяснимо квантовой теорией

В данном случае ответ на этот вопрос дает квантовая теория. В свете современных знаний механизм наследственности тесно связан с самой основой квантовой теории и, даже более того, опирается на нее. Эта теория была сформулирована Максом Планком в 1900 г. Современная генетика начинается с “открытия” менделевской работы де Фризом, Корренсом и Чермаком (1900 г.) и с работы де Фриза о мутациях (1901—1903 гг.). Таким образом, время рождения двух великих теорий почти совпадает, и не удивительно, что обе должны были достигнуть определенной степени зрелости, прежде чем между ними могла возникнуть связь. Для квантовой теории потребовалось больше четверти века, когда в 1926—1927 гг. В. Гайтлер и Ф. Лондон сформулировали основные положения квантовой теории химических связей. Гайтлер-лондоновская теория включает в себя наиболее тонкие и сложные понятия позднейшей квантовой теории, называемой квантовой механикой, или волновой механикой. Изложение ее без применения высшей математики почти невоз-

52

можно или потребовало бы по крайней мере небольшой книги. Но теперь, когда вся работа уже выполнена, становится возможным установить связь между квантовыми переходами и мутациями. Это мы и постараемся сделать.

32. Квантовая теория — дискретные состояния — квантовые переходы

Величайшее открытие квантовой теории — обнаружение дискретности в книге природы, в контексте которой, с прежней точки зрения, казалось нелепостью все, кроме непрерывности. В первую очередь это касается энергии. Тело большого масштаба изменяет свою энергию непрерывно. Например, начавший качаться маятник постепенно замедляет свое движение вследствие сопротивления воздуха. Хотя это довольно странно, но приходится принять, что система атомного порядка ведет себя иначе. Мы должны признать, что малая система в силу своей собственной природы может находиться в состояниях, различающихся только дискретными количествами энергии, которые называются ее энергетическими уровнями. Переход от одного состояния к другому представляет собой несколько таинственное явление, обычно называемое квантовым переходом.

Но энергия — не единственная характеристика системы. Возьмем снова наш маятник — тяжелый шар, который подвешен на шнуре и который может выполнять различные движения. Его можно заставить качаться с севера на юг, с востока на запад, или в любом другом направлении, или по кругу, или по эллипсу. Но если тихонько дуть на шар с помощью мехов, то можно заставить его постепенно переходить от одного вида движения к другому.

Для систем малого масштаба большинство этих или подобных характеристик (мы не можем входить в детали) изменяются прерывисто. Они “квантуются” совершенно так же, как и энергия. Поэтому, если некоторое число атомных ядер, включая и орбитальные электроны, находятся близко друг к другу и образуют “систему”, то они уже способны принимать далеко не все те произвольные конфигурации, какие мы можем себе представить. Их собственная природа оставляет им для выбора, хотя и весьма многочисленную, но прерывистую серию “состояний” *. Мы

* Я принимаю толкование, которое обычно дается в популярных книгах и которое удовлетворительно и для нашей цели, но я сам всегда осуждаю тех, кто закрепляет удобную ошибку. Истинная картина значительно сложнее, так как она включает в себя случайную индетерминантность в отношении состояния, в котором находится система.

53

обычно называем эти состояния энергетическими уровнями, так как энергия составляет весьма важную характеристику. Но надо понять, что полное описание содержит значительно больше характеристик, чем только энергию. По существу правильнее представлять себе состояние как определенную конфигурацию всех частиц. Переход из одной конфигурации в другую — это квантовый “скачок”. Если второй конфигурации соответствует большая энергия (более высокий уровень), то для перехода системы на этот уровень она должна извне получить энергию, которая не менее разности энергий, соответствующих этим состояниям. На более низкий уровень система может перейти самопроизвольно, испустив избыток энергии в виде излучения.

33. Молекулы

Система атомов может находиться в нескольких дискретных состояниях. При состоянии с наиболее низким энергетическим уровнем ядра могут сблизиться настолько, что образуется молекула. Следует подчеркнуть, что молекула обязательно будет иметь определенную устойчивость. Конфигурация ее не может изменяться по крайней мере до тех пор, пока она извне не получит такую энергию, которая необходима для “подъема” молекулы на более высокий энергетический уровень. Таким образом, устойчивость молекулы количественно оценивается разностью энергии двух конфигураций молекулы, которая, как мы увидим, является совершенно определенной величиной. Этот факт тесно связан с самой основой квантовой теории, а именно с дискретностью схемы энергетических уровней.

Я должен просить читателя принять на веру, что эта система идей была полностью подтверждена данными химии, и она блестяще оправдала себя при объяснении валентности и многих других деталей, касающихся структуры молекул, энергии их связи, их устойчивости при различных температурах и т. д. Я говорю об известной гайтлер-лондоновской теории, которая, как я сказал, не может быть изложена здесь детально.

34. Их устойчивость зависит от температуры

Мы должны ограничиться рассмотрением явления, наиболее интересного с точки зрения биологии, а именно: проанализировать устойчивость молекул при разных температурах. Примем для начала, что наша система атомов действительно находится в наиболее низкоэнергетическом состоянии. Физик назвал бы ее молекулой при температуре, равной абсолютному нулю. Что-

54

бы поднять молекулу на ближайший более высокий уровень, необходимо снабдить ее определенным количеством энергии. Проще всего это сделать, если “нагреть” молекулу. Вы помещаете ее в условия более высокой температуры (тепловую баню), позволяя таким образом другим системам (атомам, молекулам) ударяться о нее.

Из-за полной хаотичности теплового движения нельзя точно указать температуру, при которой непременно и немедленно произойдет “переход” молекулы в другое состояние. Вернее, при всякой температуре (выше абсолютного нуля) имеется определенная, большая или меньшая, вероятность подъема ее на новый уровень, причем эта вероятность, конечно, увеличивается с повышением температуры. Наилучший способ выразить эту вероятность — указать среднее время, которое следует выждать, пока произойдет этот подъем, то есть указать “время ожидания”.

По данным М. Поланьи и Е. Вигнера *, время ожидания зависит преимущественно от отношения двух энергий. Одна из них — та разность энергий, которая необходима для подъема молекулы на следующий уровень (назовем ее W), а другая характеризует интенсивность теплового движения при данной температуре (обозначим абсолютную температуру буквой Т, а эту характеристику — kT) **. Понятно, что вероятность подъема молекулы на новый уровень тем меньше и, значит, время ожидания тем больше, чем выше сам уровень по сравнению со средней тепловой энергией, иначе говоря, чем выше отношение W/kT. Самое удивительное это то, что время ожидания сильно зависит от сравнительно малых изменений отношения W/kT. Например (по Дельбрюку), для W, которое в 30 раз больше kT, время ожидания будет всего 0,1 секунды, но оно повышается до 16 месяцев, когда ТУ в 50 раз больше kT, и до 30 000 лет, когда ТУ в 60 раз больше kT!

35. Математическое отступление

По-видимому, имеет смысл выразить на математическом языке (для тех читателей, кому это доступно) причину такой огромной чувствительности к изменениям в уровнях или температуре и сделать несколько физических замечаний. Причина чувствительности в том, что время ожи-

* Zeitschrift fur Physik, Chemie (A), Haber— Band, S. 439, 1928.

** k — постоянная Больцмана, величина которой известна; 3/2 kT — средняя кинетическая энергия атома газа при темпераратуре Т.

55

дания, назовем ею t, зависит от отношения W/kT как экспоненциальная функция, то есть t = τe^W/kT.

При этом τ — некоторая малая константа порядка 10^-13 или 10^-14 секунды. Так вот, эта экспоненциальная функция не случайная величина. Она многократно встречается в статистической теории термодинамики, образуя как бы ее спинной хребет. Это — мера невероятности того, что количество энергии, равное W, может случайно скопиться в некоторой определенной части системы, и именно эта невероятность возрастает так сильно, что требуется многократное превышение средней энергии kT *.

Действительно, W = 30 kT (пример, приведенный выше) — крайне редкий случай. То, что это не ведет к очень долгому времени ожидания (только 0,1 секунды в нашем примере), объясняется, конечно, малой величиной множителя τ.

Этот множитель имеет физический смысл. Его величина соответствует порядку периода колебаний, все время происходящих в системе. Вы могли бы, вообще говоря, сказать: этот множитель означает, что вероятность накопления требуемой величины W, хотя и очень мала, повторяется снова и снова “при каждом колебании”, то есть около 10¹³ или 10¹⁴ раз в течение каждой секунды.

36. Первое уточнение

Предлагая эти соображения как теорию устойчивости молекул, мы молчаливо приняли, что квантовый переход, называемый нами подъемом, ведет если не к полной диссоциации, то, по крайней мере, к существенно иной конфигурации тех же атомов — к изомерной молекуле, как сказал бы химик, то есть к молекуле, состоящей из тех же атомов, но связанных в другом порядке (в приложении к биологии это может быть новый аллель того же локуса, а квантовый переход будет соответствовать мутации).

Чтобы согласиться с такой интерпретацией, в нашем изложении следует исправить два момента, которые я намеренно упростил, желая сделать изложение более понятным. На основании сказанного выше можно было бы подумать, что только в самом низком энергетическом состоянии группа атомов образует то, что мы называем молекулой, и даже ближайшее более высокое состояние уже является чем-то другим. Но это не так. В действительности за самым низким энергетическим электронным уровнем следу-

* Чтобы преодолеть порог W.— Прим. перев.

56

ет серия уровней, не связанных с каким-либо заметным изменением конфигурации в целом, но соответствующих тем незначительным колебаниям атомов, о которых мы упомянули в § 35. Они (эти колебания) также “квантуются”, по различие в энергии этих уровней невелико. Следовательно, удары частиц тепловой бани могут быть достаточными, чтобы переводить молекулу на эти уровни уже при довольно низкой температуре. Если молекула представляет собой растянутую структуру, вы можете представить эти колебания в виде высокочастотных звуковых волн, пересекающих молекулу, не причиняя ей вреда.

Таким образом, первое уточнение не особенно серьезно. Мы должны пренебречь “тонкой колебательной структурой” в схеме уровней. Термин “следующий, более высокий уровень” надо понимать как следующий уровень, соответствующий известному изменению конфигурации.

37. Второе уточнение

Второе уточнение объяснить значительно труднее потому, что оно касается некоторых весьма важных, но довольно сложных особенностей схемы интересующих нас различных уровней. Свободный переход от одного из них к другому может быть затруднен совершенно независимо от требующейся дополнительной энергии. В действительности затруднение не исключается даже при переходе от более высокого к более низкому уровню.

Начнем с эмпирических фактов. Химику известно, что одна и та же группа атомов при образовании молекул может объединиться более чем одним способом. Такие молекулы называются изомерными (состоящими из тех же частей; ισος — ςот же, μεροςi — χасть). Изомерия не исключение, она является правилом. Чем больше молекула, тем больше возможных изомеров. На рис. 16 показан один из простейших случаев: каждый из двух изомеров пропилового спирта состоит из трех атомов углерода С, восьми атомов водорода H и одного атома кислорода О.

Рис. 16. Два изомера пропилового алкоголя

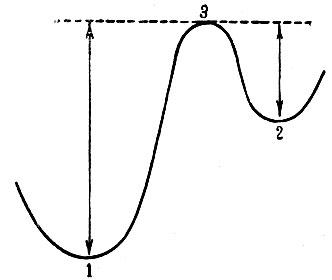
Атом кислорода может быть расположен (вставлен) между любым атомом водорода и соседним атомом углерода. Но только в двух случаях, показанных на рисунке, образуются разные вещества. И они действительно разные. Все их физические и химические свойства четко различаются. Так же различны и их энергии — они представляют собой “различные уровни”.

Замечателен тот факт, что обе молекулы весьма устойчивы. Обе ведут себя так, как если бы они были “нижними

57

уровнями”. Самопроизвольных переходов из одного состояния в другое не происходит.

Причина здесь та, что обе конфигурации не являются соседними. Переход от одной к другой может происходить только через промежуточные конфигурации, соответствующие уровням с более высокой энергией, чем у каждой из этих двух. Говоря грубо, кислород должен быть извлечен из одного положения и вставлен в другое (новое). По-видимому, не существует способа сделать это, минуя конфигурации со значительно более высокими энергетическими уровнями. Это положение можно наглядно изобразить графически так, как на рис. 17, где цифрами 1 и 2 обозначены два состояния или два изомера, цифрой 3 — “потенциальный барьер” между ними, две стрелки показывают подъем, то есть значения энергии, необходимой для того, чтобы произошел переход от состояния 1 к состоянию 2 или от состояния 2 к состоянию 1.

Рис. 17. Энергетический порог 3 между изомерными уровнями 1 и 2. Стрелки указывают минимум энергии, требующейся для перехода

Теперь мы можем сделать второе уточнение, сводящееся к тому, что в применении к биологии нас будут интересовать переходы только такого изомерного типа. Именно их мы и подразумевали, когда объясняли состояние устойчивости в § 33—35. Квантовый переход, который мы имели в виду, — это переход от одной относительно устойчивой молекулярной конфигурации к другой. Энергия, необходимая для перехода (обозначенная нами W), в действительности является не разностью энергий уровней, а ступенькой от исходного уровня до потенциального барьера (см. стрелки на рис. 17).

Переходы без преодоления потенциального барьера между исходным и конечным состояниями совершенно не представляют интереса и не только применительно к биологии. Они абсолютно ничего не меняют в химической устойчивости молекул. Почему? Они не дают продолжительного эффекта и остаются незамеченными, ибо когда такой переход происходит, за ним почти немедленно следует возвращение в исходное состояние, поскольку ничто не препятствует этому.

58