|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Закон квадрата — куба |
Закон квадрата — куба
 Например, куб с длиной стороны 1 метр имеет площадь поверхности 6 м² и объём 1 м³. Если длину стороны удвоить, площадь его поверхности увеличится в четыре раза — до 24 м², а его объём увеличится в 8 раз — до 8 м³. Этот принцип применим ко всем телам. Этот закон находит своё применение в технике и биомеханике. Его первым продемонстрировал Галилео Галилей в 1638 году в «Беседы и математические доказательства двух новых наук». Сопромат Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится пропорционально коэффициенту увеличения в третьей степени, в то время как площадь его поверхности — квадрату масштабного множителя. Это, в частности, означает, что, если сегменту поверхности увеличенного в размерах объекта, сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление. При увеличении размеров объекта с сохранением того же самого материала, из которого состоит объект, (а значит, и плотности) и ускорения давление, производимое им на поверхность, увеличится во столько же раз. Отсюда видно, что при увеличении объекта у него снизится способность сопротивляться напряжению и его окажется легче разрушить в процессе ускорения. Это объясняет то, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях и почему есть пределы высоты строительства высотных зданий. Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление. Биомеханика Если размеры животного значительно увеличить, его мускульная сила серьёзно уменьшится, так как поперечное сечение его мускулов увеличится пропорционально квадрату коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу этого коэффициента. По этой причине, к примеру, насекомые могут поднимать вес, значительно превышающий свой собственный. Если летающих живых существ увеличить в размерах, их нагрузка на крылья должна возрасти, и поэтому им, чтобы сохранять ту же подъёмную силу, придётся махать с большей частотой. Это будет нелегко из-за того, что сила мускулов станет меньше. Это также объясняет, почему шмель может иметь размер тела, большой по сравнению с размахом его крыльев, тогда как для летающего животного, значительно большего, чем шмель, это было бы невозможно. Также для живых существ малых размеров велико сопротивление воздуха на единицу массы, и поэтому они не погибают, падая с любой высоты. Кроме того, работа дыхательной системы насекомых зависит от величины поверхности тела. При увеличении объёма тела площадь его поверхности не сможет обеспечивать дыхание. По этим причинам гигантские насекомые, пауки и другие животные, показываемые в фильмах ужасов, нереальны, поскольку такие крупные размеры вызвали бы их удушье и разрушение. Исключением являются гигантские водные животные (глубоководный гигантизм), так как вода способна поддерживать достаточно огромные существа. Дж. Б. С. Холдейн высказал следующее мнение по поводу великанов: Допустим, что существует человек-великан 60-ти футов высотой, как из сказок моего детства. Такие великаны не только в 10 раз выше среднего человека, но в 10 раз шире и в 10 раз плотнее, то есть их общий вес в 1000 раз превышает вес среднего человека, а следовательно, составляет от 80 до 90 тонн. Поперечный срез костей таких великанов в 100 раз превышает срез костей среднего человека; следовательно, каждый квадратный дюйм кости гиганта должен выдержать нагрузку в 10 раз большую, чем квадратный дюйм кости среднего человека. Учитывая, что берцовая кость человека разрушается при нагрузке, в 10 раз превышающей его вес, берцовая кость великанов должна была бы ломаться при каждом их шаге. Уж не потому ли на картинках, которые я ещё помню, они изображены сидящими? Тепловые процессы Закон квадрата — куба также применим к тепловым процессам: поверхность теплообмена возрастает пропорционально квадрату размера, а объём, содержащий или генерирующий теплоту, — пропорционально кубу. Следовательно, теплопотери в расчёте на единицу объёма объекта уменьшаются при увеличении его размеров и, наоборот, увеличиваются при уменьшении размеров. Поэтому, например, энергия, необходимая для обогрева или охлаждения единицы объёма помещения, уменьшается с ростом размеров помещения. Двигатели внутреннего сгорания Если просто увеличить все размеры двигателя внутреннего сгорания в a раз при неизменной частоте вращения, то масса движущихся частей увеличится в a³ раз, а ускорение, с которым они движутся, — в a раз. Следовательно, все силы инерции увеличатся в a⁴ раз, а, поскольку площадь трущихся поверхностей увеличится только в a² раз, удельная нагрузка на них увеличится в a² раз, что приведёт к их быстрому износу. Кроме того, в a раз увеличится скорость движения газов через клапаны, что значительно увеличит газодинамическое сопротивление и ухудшит наполнение цилиндров. Поэтому при пропорциональном увеличении ДВС приходится пропорционально уменьшать частоту вращения (сохраняя неизменной среднюю скорость поршня). Тогда остаются неизменными удельная нагрузка на трущиеся поверхности и скорость движения газов через клапаны. Однако удельная мощность (на единицу массы) и литровая мощность при этом пропорционально уменьшаются. Разрешить такое «утяжеление» двигателя можно путём увеличения числа цилиндров, однако это усложняет его конструкцию. Судостроение Приближённо можно считать, что сопротивление движению судна (при неизменной скорости) пропорционально площади поперечного сечения корпуса на миделе. Таким образом, при увеличении всех размеров судна в a раз его масса вырастет в a³ раз, а сопротивление движению только в a² раз. Следовательно, в плане расхода топлива на единицу массы экономичнее более крупные суда. Кроме того, если доля запасов топлива в общей массе судна неизменна, то дальность плавания без дозаправки также увеличится в a раз.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Закон квадрата — куба |
|
[time: 438 ms; queries: 7]
22 Фев 2026 01:22:14 GMT+3 |


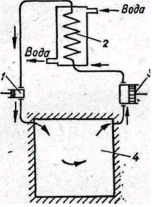 Воздух как хладагент безвреден, общедоступен, безопасен и почти нейтрален к металлам и смазочным маслам, поэтому его применение в холодильной технике весьма удобно. Однако его недостатком является малая объемная холодопроизводительность.
Воздух как хладагент безвреден, общедоступен, безопасен и почти нейтрален к металлам и смазочным маслам, поэтому его применение в холодильной технике весьма удобно. Однако его недостатком является малая объемная холодопроизводительность. Электродвигатель постоянного тока. Универсальный электродвигатель постоянного и переменного тока. Электродвигатель постоянного тока с тремя катушками. Бесщеточный электродвигатель постоянного тока. Шаговый электродвигатель. Асинхронный электродвигатель. Вращающееся магнитное поле и синхронная скорость. Однофазный асинхронный электродвигатель. Подключение по схеме «звезда» и «треугольник». Синхронный электродвигатель. Генератор переменного тока.
Электродвигатель постоянного тока. Универсальный электродвигатель постоянного и переменного тока. Электродвигатель постоянного тока с тремя катушками. Бесщеточный электродвигатель постоянного тока. Шаговый электродвигатель. Асинхронный электродвигатель. Вращающееся магнитное поле и синхронная скорость. Однофазный асинхронный электродвигатель. Подключение по схеме «звезда» и «треугольник». Синхронный электродвигатель. Генератор переменного тока. В научных представлениях о происхождении жизни в последнее десятилетие происходит настоящая революция, и она далеко не завершена. К сожалению, эта информация доступна в основном только на английском языке. Цикл статей, предлагаемый вниманию читателей, отчасти восполнит этот пробел.
В научных представлениях о происхождении жизни в последнее десятилетие происходит настоящая революция, и она далеко не завершена. К сожалению, эта информация доступна в основном только на английском языке. Цикл статей, предлагаемый вниманию читателей, отчасти восполнит этот пробел. В 1936 году советский инженер и учёный Владимир Лукьянов создал вычислительную машину, все математические операции в которой выполняла текущая вода. Гидравлический интегратор Лукьянова — первая в мире вычислительная машина для решения дифференциальных уравнений в частных производных — на протяжении полувека был единственным средством вычислений, связанных с широким кругом задач математической физики.
В 1936 году советский инженер и учёный Владимир Лукьянов создал вычислительную машину, все математические операции в которой выполняла текущая вода. Гидравлический интегратор Лукьянова — первая в мире вычислительная машина для решения дифференциальных уравнений в частных производных — на протяжении полувека был единственным средством вычислений, связанных с широким кругом задач математической физики. С развитием технологий растет и потребление энергии. Что же делать человечеству, когда на Земле ее перестанет хватать? Еще в 1959 году американский физик-теоретик Фримен Дайсон предложил гипотетическое астроинженерное сооружение — оболочку вокруг Солнца радиусом 1 а.е. и толщиной 3 м. По задумке, сфера Дайсона позволила бы решить проблему нехватки энергии и перенаселения.
С развитием технологий растет и потребление энергии. Что же делать человечеству, когда на Земле ее перестанет хватать? Еще в 1959 году американский физик-теоретик Фримен Дайсон предложил гипотетическое астроинженерное сооружение — оболочку вокруг Солнца радиусом 1 а.е. и толщиной 3 м. По задумке, сфера Дайсона позволила бы решить проблему нехватки энергии и перенаселения. Словарь отвечает на многие вопросы из области техники, рассказывает об истории ее развития и научно-техническом прогрессе, об известных ученых и наиболее выдающихся открытиях. Книга охватывает большой круг знаний — от космической техники до техники кино и телевидения, рассказывает о многих профессиях. В ней содержатся практические советы юным техникам. Для школьников среднего и старшего возраста.
Словарь отвечает на многие вопросы из области техники, рассказывает об истории ее развития и научно-техническом прогрессе, об известных ученых и наиболее выдающихся открытиях. Книга охватывает большой круг знаний — от космической техники до техники кино и телевидения, рассказывает о многих профессиях. В ней содержатся практические советы юным техникам. Для школьников среднего и старшего возраста.