|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Отчего у леопарда пятна на шкуре // Дж. Д. Марри |
Отчего у леопарда пятна на шкуреДж. Д. Марри
Возможно, в основе широкого разнообразия раскрасок шкуры у животных, наблюдаемого в природе, лежит единый механизм формирования таких структур. Результаты математического моделирования этого механизма открывают биологам новые перспективы для исследований.
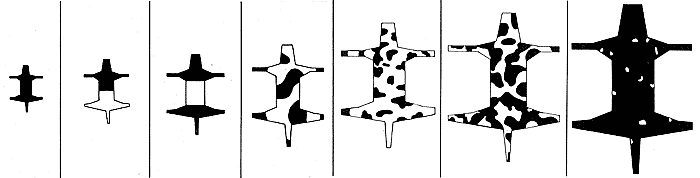
Млекопитающие демонстрируют исключительное разнообразие структур раскраски шкуры. Для этого было предложено много объяснений, но большинство из них настолько же "убедительны", как и чудесная сказка Редьярда Киплинга "Отчего у леопарда пятна на шкуре". Хотя установлено, что гены управляют процессами, протекающими при формировании структуры (узоров) раскраски шкуры, реальные механизмы, которые ее определяют, пока не известны. Как с точки зрения эволюционной биологии, так и с точки зрения биологии развития было бы замечательно, если бы оказалось, что в основе огромного разнообразия раскрасок шкуры у животных, наблюдаемого в природе, лежит единый механизм. Я сделал предположение, что большинство (если не все) из наблюдаемых типов структур раскраски шкуры у животных могут действительно определяться одним механизмом их формирования. В данной статье кратко описана простая математическая модель образования этих структур в процессе развития зародыша. Важная особенность заключается в том, что структуры, полученные с ее помощью, поразительно напоминают раскраску шкуры у многих животных, таких как леопард, гепард, ягуар, зебра и жираф. Эта модель согласуется также с тем наблюдением, что, хотя распределение пятен у представителей семейства кошачьих и полос у зебр сильно различается и сугубо индивидуально, каждый тип распределения придерживается как бы общей закономерности. Кроме того, модель предсказывает, что такие структуры могут иметь лишь определенные формы. Это в свою очередь предполагает наличие некоторых запретов на их возможное развитие и позволяет понять, каким образом структуры раскраски шкуры могли эволюционировать. Пока с полной достоверностью не установлено, что именно происходит в процессе развития зародыша и вы-зывет образование узоров на шкуре у животных. В настоящее время имеется несколько вероятных механизмов их формирования. Привлекательность нашей модели заключается в ее математическом богатстве и поразительной способности давать структуры, соответствующие наблюдаемым в природе. Я надеюсь, что эта модель подтолкнет экспериментаторов к дальнейшим исследованиям, что в конечном счете поможет установить биологический механизм образования различной раскраски шкуры у животных. КОНЕЧНО, нельзя сказать, что о природе узоров на шкуре у животных ничего не известно. Пятна на шкуре у млекопитающих соответствуют областям по-разному окрашенных волос. Цвет волос определяется специализированными пигментными клетками, называемыми меланоцитами, которые находятся в базальном (наиболее глубоком) слое эпидермиса. Меланоциты вырабатывают пигмент, называемый меланином, который затем переходит в волосы. У млекопитающих есть в основном только два вида меланина: эумеланин (от греческих слов "эу" - хороший и "мелас" - черный), окрашивающий волосы в черный или коричневый цвет, и феомеланин (от "феос" - пыльный), который делает волосы желтыми или рыжими. Предполагают, что меланоциты производят или не производят меланин в зависимости от наличия или отсутствия химических активаторов или ингибиторов. Хотя пока не известно, что это за вещества, считают, что каждый имеющийся на шкуре узор отражает лежащую в его основе предварительную химическую структуру. Эта предварительная структура (предструктура), если она существует, должна возникать внутри эпидермиса или сразу под ним. При этом меланоциты как бы "считывают" предструктуру. Модель, которая описывается в данной статье, способна генерировать такую предструктуру. Моя работа основана на модели, разработанной А. Тьюрингом (который ввел концепцию абстрактной "вычислительной машины" - так называемой машины Тьюринга; его труды способствовали созданию современных ЭВМ). В 1952 г. в одной из наиболее важных в теоретической биологии работ Тьюринг ввел химический механизм возникновения узоров на шкуре у животных. Он предположил, что биологическая форма определяется предструктурой, образованной неравномерным распределением (концентрацией) химических веществ, которые он назвал морфогенами. Существование морфогенов до настоящего времени окончательно не установлено, за исключением некоторых косвенных подтверждений. Тем не менее модель Тьюринга до сих пор представляет интерес, поскольку она позволяет объяснить множество экспериментальных результатов с помощью одной или двух простых идей. Тьюринг начал с предположения о том, что морфогены могут реагировать друг с другом и диффундировать через клетки. Затем он разработал математическую модель, в которой показал, что если морфогены реагируют и диффундируют определенным образом, то из первоначально однородного распределения в скоплении клеток могут возникнуть пространственные структуры в распределении морфогенов. Модель Тьюринга породила целый класс моделей, которые теперь относят к моделям реакционно-диффузионного типа. Эти модели применимы в тех случаях, когда размер пространственной структуры велик по сравнению с размером отдельных клеток, например для шкуры леопарда, поскольку в пятне на его шкуре в момент возникновения структуры имеется, вероятно, около 100 клеток. Первоначальная работа Тьюринга была развита рядом исследователей, в том числе и мною, в более завершенную математическую теорию. В типичной реакционно-диффузионной модели начинают с того, что вводят два морфогена, которые реагируют друг с другом и диффундируют с различными скоростями. В отсутствие диффузии (например, в случае идеального перемешивания) в результате реакции между двумя морфогенами система должна достигнуть однородного стационарного состояния. Если теперь позволить морфогенам диффундировать с одинаковыми скоростями, то любое пространственное отклонение от этого устойчивого состояния будет сглаживаться. Однако, если скорости диффузии не равны, диффузия может оказывать дестабилизующее влияние: скорости реакции в любой заданной точке могут не успеть достаточно быстро "подстроиться", чтобы система достигла равновесия. Если условия выбраны правильно, то малое пространственное возмущение может стать неустойчивым и начинает расти пространственная структура. Говорят, что такая неустойчивость обусловлена диффузией. В РЕАКЦИОННО-ДИФФУЗИОННЫХ моделях предполагается, что один из морфогенов, является активатором, который заставляет меланоциты производить меланин какого-либо вида, например черного, а другой - ингибитором, дающим команду пигментным клеткам не вырабатывать меланин. Предположим, что в этих реакциях активатор локально увеличивает свою концентрацию и одновременно производит ингибитор. Если ингибитор диффундирует быстрее активатора, то образуется "остров" высокой концентрации активатора в области высокой концентрации ингибитора. Некоторое представление о том, как такой активаторно-ингибиторный механизм может создать пространственные структуры в распределении концентрации морфогенов, можно получить из следующей аналогии. Пусть имеется очень сухой лес, иными словами, есть все условия для лесного пожара. Чтобы свести к минимуму возможный урон, по всему лесу рассредоточены пожарные с противопожарным снаряжением и вертолеты. Теперь представим, что вспыхивает пожар (активатор). От места воспламенения начинает двигаться фронт огня. Первоначально поблизости от места пожара недостаточно пожарных (ингибитора), чтобы погасить огонь. Однако с помощью вертолетов пожарные могут обогнать фронт огня и обработать деревья реактивами, которые не позволят им загореться. Когда огонь достигнет обработанных деревьев, он погаснет. Фронт остановится. Если пожары спонтанно возникают в разных местах леса, то через какое-то время сформируются несколько распространяющихся фронтов огня (волн активации). В свою очередь это заставит пожарных на вертолетах (волны ингибирования) обогнать каждый фронт и остановить его на некотором расстоянии от места воспламенения. Конечным результатом такого сценария будет лес с черными пятнами сгоревших деревьев, перемежающимися с пятнами зеленых нетронутых деревьев. В принципе полученная картина имитирует результат, даваемый реакционно-диффузионными механизмами, обусловленными диффузией. Тип образующейся структуры зависит от различных параметров модели и может быть получен из математического анализа. Предложено много конкретных реакционно-диффузионных моделей, основанных на гипотетических или реальных биохимических реакциях, и исследованы их возможности давать пространственные структуры. Эти механизмы включают несколько параметров: скорости реакций, скорости диффузии реагентов и (что особенно важно) геометрию и размеры живой ткани. Поразительное свойство реакционно-диффузионных моделей заключается в тех конечных результатах, которые получаются из первоначально однородного состояния при условиях, когда меняется только один параметр, а остальные фиксированы. Например, предположим, что меняется размер живой ткани. Тогда в какой-то момент времени будет достигнута критическая величина, называемая бифуркационной точкой, в которой однородное стационарное состояние морфогенов становится неустойчивым, и начинает расти пространственная структура. Наиболее наглядный пример реакционно-диффузионного механизма образования пространственных структур представляют колебательные химические реакции, открытые советскими учеными Б.П. Белоусовым и А.М. Жаботинским в конце 50-х годов. Эти реакции могут быть организованы в пространстве и во времени в форме кольцевых волн. Они могут сопровождаться периодическими колебаниями с точностью часового механизма, что наблюдается по изменению цвета реакционной смеси, например, от голубого до оранжевого и обратно до голубого дважды в течение минуты. Другой тип реакционно-диффузионных структур в природе был открыт и исследован французским химиком Д. Томасом в 1975 г. Эти структуры возникают при реакции между мочевой кислотой и кислородом на тонкой мембране, внутри которой они могут диффундировать. Хотя мембрана содержит иммобилизированный фермент, катализирующий реакцию, в эмпирическую модель, описывающую ее механизм, входят только два реагента, а фермент не включен. Кроме того, поскольку мембрана тонкая, можно предположить, что процесс протекает в двумерном пространстве. Я полагаю, что достойным кандидатом для универсального механизма, генерирующего предструктуру раскраски шкуры у млекопитающих, является реакционно-диффузионная система, в которой могут развиваться пространственные структуры, обусловленные диффузией. Такие структуры существенно зависят от геометрии и размеров области, в которой протекает соответствующая химическая реакция. Следовательно, величина и форма зародыша в тот момент, когда активируются реакции, должны определять получившуюся пространственную структуру. (Последующий рост может исказить первоначальную структуру.) ЛЮБОЙ реакционно-диффузионный механизм, обусловливающий возникновение пространственных структур, мог бы быть подходящей моделью для формирования раскраски шкуры у животных. Численные и математические результаты, которые я привожу в этой статье, основаны на модели, вытекающей из работы Томаса. При использовании типичных значений параметров время формирования раскраски шкуры в процессе эмбриогенеза составляет около суток. Интересно, что математическая задача описания начальных стадий формирования пространственной структуры с помощью реакционно-диффузионных механизмов (когда отклонение от однородного состояния невелико) аналогична математической задаче описания колебаний тонких пластинок или поверхности барабана. Таким образом, характер зависимости роста структуры от ее геометрии и размеров можно понять, рассматривая аналогичные вибрирующие поверхности. Если поверхность очень мала, она не сможет поддерживать колебания и возмущения быстро затухнут. Следовательно, чтобы возбудить незатухающее колебание, необходима поверхность определенного размера. Предположим, что поверхность, соответствующая реакционно-диффузионной области, имеет прямоугольную форму. По мере увеличения размеров прямоугольника возникает набор все более усложняющихся мод возможных колебаний. Важным примером того, как геометрия ограничивает эти колебательные моды, является ситуация, когда область настолько узка, что могут существовать только простые - по существу одномерные - моды. Для истинно двумерных структур нужна область, имеющая достаточно большие как длину, так и ширину. Аналогичное требование для колебаний на поверхности цилиндра заключается в том, что его радиус не может быть слишком мал, в противном случае могут существовать только квазиодномерные моды; другими словами, могут образовываться только кольцеобразные структуры. Однако, если радиус достаточно велик, на поверхности могут существовать двумерные структуры. Следовательно, сужающийся цилиндр может демонстрировать переход от двумерной структуры к простым полосам (см. рисунок ниже). Для реакционно-диффузионного механизма с двумя морфогенами я выбрал такой набор параметров реакций и диффузии, который соответствует диффузионной неустойчивости, и сохранил их неизменными при всех вычислениях. Изменялись только размеры и геометрия рассматриваемой области. При моделировании на компьютере в качестве начальных условий я выбирал случайные возмущения однородного стационарного состояния. Темные или светлые области получившейся структуры - это те, в которых концентрация одного из морфогенов соответственно больше или меньше его концентрации в однородном стационарном состоянии. Даже при таких ограничениях на параметры и начальные условия богатство возможных структур поразительно. Как результаты модели соотносятся с типичными узорами на шкуре и общими признаками, обнаруживаемыми у животных? Я начал с рассмотрения сужающихся цилиндров, чтобы смоделировать узоры на хвостах и лапах животных. Результаты аналогичны тем, что были получены для вибрирующей поверхности: если двумерная область, покрытая пятнами, становится достаточно узкой, то пятна постепенно переходят в полосы. Леопард (Panthera pardus), гепард (Acinonyx jubatus), ягуар (Panthera оncа) и генета (Genetta genetta) дают хорошие примеры таких структур. Пятна на шкуре у леопарда доходят почти до кончика хвоста. Хвосты у гепарда и ягуара имеют отчетливо выраженные полосатые участки, а у генеты хвост полностью полосатый. Эти наблюдения согласуются с тем, что известно о зародышах этих четырех животных. Хвост у зародыша леопарда резко сужается и сравнительно короткий, поэтому можно ожидать, что на нем могут сохраняться пятна до самого его кончика. (У взрослого леопарда хвост длинный, но в нем столько же позвонков.) Хвост у зародыша генеты соответствует другому крайнему случаю: он имеет почти постоянный, причем довольно малый, диаметр, поэтому на хвосте генеты должны возникать поперечные полосы. Модель дает также пример запрета на структуры определенного типа, которые действительно наблюдаются у животных исключительно редко. Если в основе механизма формирования предструктуры раскраски шкуры у животных лежит реакционно-диффузионный процесс (или любой другой процесс, который аналогичным образом зависит от размеров и геометрии), запрет обусловлен размерами и геометрией зародыша. В частности, модель допускает, что пятнистое животное может иметь полосатый хвост, но у полосатого животного не может быть пятнистого хвоста. Мы добились успеха также в попытках понять, как возникает узор на шкуре у зебры. С помощью использованного нами механизма нетрудно получить набор полос. Более сложной является область соединения передней ноги и туловища, однако математическая модель верно предсказывает типичную картину полос в области лопаток (см. рисунок ниже). Чтобы изучить влияние размеров в случае более сложной геометрии, мы рассчитали структуры для обобщенной формы животного, состоящей из тела, головы, четырех конечностей и хвоста (см. рисунки внизу). Мы начинали с маленькой фигуры и постепенно увеличивали ее размер, сохраняя все пропорции. Получено несколько интересных результатов. Если рассматриваемая область очень мала, не возникает никаких структур. По мере увеличения ее размеров происходят последовательные бифуркации: различные узоры внезапно возникают и пропадают. При дальнейшем увеличении размеров структуры получаются более сложными и с большим числом пятен. Однако в случае удлиненной узкой формы полосатый узор сохраняется даже тогда, когда область становится довольно большой. При очень больших размеpax области структура узора делается столь мелкой, что окраска становится опять почти однородной по цвету.
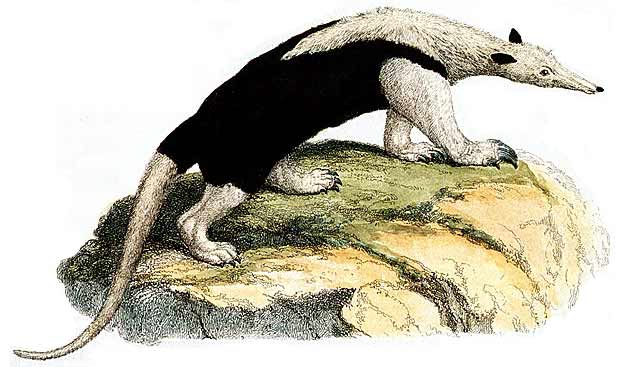
ЕСЛИ реакционно-диффузионная модель справедлива, то для объяснения влияния размеров зародыша животного на структуру раскраски его шкуры первостепенное значение имеет момент времени, в который активируется механизм формирования этой структуры в процессе эмбриогенеза. Мы ввели неявное предположение, что соответствующие константы скоростей реакции и диффузионные коэффициенты примерно одинаковы для разных животных. Если механизм активируется генетически на ранней стадии развития, тогда, например, окраска многих небольших животных, имеющих короткие сроки беременности, должна быть однородной по цвету. В общем случае это действительно так. Для поверхностей большей площади в момент активации существует возможность того, что животное наполовину будет черным и наполовину белым. Примером служит муравьед и поразительно окрашенный безоаровый козел (Capra aegagrus hircus) (см. рисунки ниже). По мере увеличения размеров одновременно должна возрастать сложность возникающей структуры. Фактически наблюдается нарастание сложности окраски от безоарового козла к зебре, а затем к леопарду и гепарду. Наконец, шкуры у очень больших животных снова должны быть однородными по цвету, что на самом деле имеет место у слонов, носорогов и бегемотов.
Мы считаем, что момент времени, в который активируется механизм формирования структуры, - наследуемое свойство, поэтому по крайней мере для животных, выживание которых в значительной степени зависит от раскраски, механизм активируется тогда, когда зародыш достигает определенного размера. Конечно, условия на поверхности зародыша в момент активации носят в некоторой степени случайный характер. Реакционно-диффузионная модель дает структуры, которые однозначно зависят от начальных условий, геометрии и размеров. Важная особенность этого механизма заключается в том, что при заданных геометрии и размерах получающиеся структуры для разных случайных начальных условий качественно одинаковы. Например, если структура пятнистая, то меняется только распределение пятен. Этот результат согласуется с тем, что внутри одного вида узор на шкуре животного индивидуален. Такая индивидуальность учитывает отличительные особенности семейства, а также общие групповые особенности. Предполагают, что моделируемые структуры соответствуют пространственным структурам в распределении морфогенов. Если их концентрация достаточно высока, меланоциты будут вырабатывать пигмент меланин. Для упрощения мы считали, что однородное стационарное состояние соответствует пороговой концентрации и что меланин будет вырабатываться, если концентрация морфогенов равна или больше этой величины. Однако это предположение несколько произвольно. По-видимому, пороговая концентрация может меняться даже внутри одного вида. Чтобы исследовать такие эффекты, были рассмотрены разновидности жирафа. Для заданного характера структуры изменялся параметр, соответствующий пороговой концентрации морфогена для производства меланина. Меняя этот параметр, мы обнаружили, что можем получать структуры, явно напоминающие узоры на шкурах жирафов двух разновидностей (см. рисунок ниже).
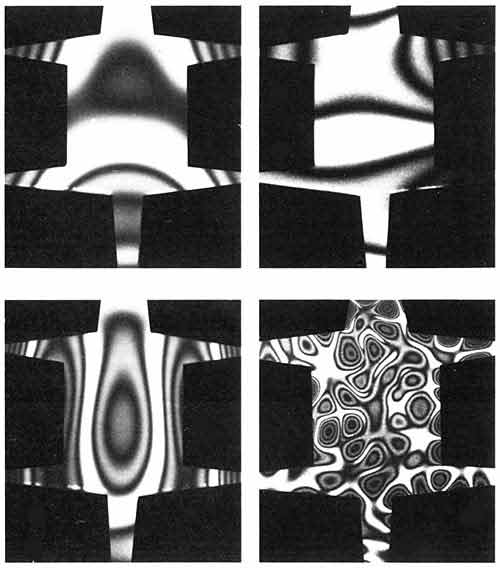
НЕДАВНО наши результаты нашли неожиданное подтверждение в работах Ч, Веста и Сюй Юженя из Мичиганского университета. Они создавали стоячие волны на вибрирующей пластинке и изменяли вид возникающих структур, меняя частоту колебаний. Структуры становились видимыми с помощью голографии, когда пластинка освещалась лучом лазера. Отраженный от нее свет интерферировал с опорным лучом, так что гребни волн складывались с гребнями, впадины-с впадинами, а впадины и гребни взаимно уничтожались. Возникающая картина фиксировалась на фотопластинке (см. рисунок внизу).
Вест и Сюй Южень обнаружили, что низкие частоты колебаний создают простые структуры, а высокие - сложные структуры. Это наблюдение представляет интерес, поскольку было показано, что если структура образуется на пластинке, колеблющейся с заданной частотой, то структура, образующаяся на той же пластинке, колеблющейся с большей частотой, идентична структуре, образующейся на пропорционально увеличенной пластинке, колеблющейся с первоначальной частотой. Таким образом, данные Веста и Сюй Юженя подтверждают вывод о том, что по мере увеличения размеров реакционно-диффузионной области должны возникать все более сложные структуры. Сходство между нашими структурами и структурами, полученными исследователями из Мичиганского университета, поразительно. Я бы хотел еще раз подчеркнуть, что все структуры были получены только за счет изменения размеров и геометрии реакционной области; все другие параметры были фиксированы (за исключением различных пороговых концентраций в случае жирафа). Даже в этих условиях разнообразие структур замечательно. Модель предлагает также возможное объяснение различных аномалий в раскраске, наблюдаемых у ряда животных. При некоторых условиях изменение величины одного из параметров может вызвать заметное изменение получаемой структуры. Величина этого эффекта зависит от того, насколько близко значение параметра к бифуркационной точке - значению, при котором возникает качественное изменение генерируемой структуры. Если один из параметров, например константа скорости в реакционной кинетике, непрерывно меняется, то реакционно- диффузионный механизм переходит от состояния, в котором не могут возникать никакие структуры, к состоянию, в котором структуры генерируются, и, наконец, обратно к состоянию без структур. Тот факт, что такие малые изменения параметра около бифуркационной точки могут вызвать столь значительные изменения в структуре, согласуется с теорией эволюции, известной под названием "прерывистое равновесие". Согласно этой теории, длительные периоды малых эволюционных изменений прерываются короткими всплесками внезапных и быстрых изменений. НА РАСКРАСКУ шкуры у животных, безусловно, влияют многие факторы. Некоторые из них - это температура, влажность, питание, гормоны и интенсивность метаболизма. Хотя влияние таких факторов, вероятно, можно имитировать, используя различные параметры, в этом нет особого смысла, пока не станет больше известно о том, как действительно образуются структуры, отображаемые меланиновыми пигментами. В то же время нельзя не отметить широкого разнообразия структур, которые могут быть получены из реакционно-диффузионной модели при изменении только размеров и геометрии. Вселяет энтузиазм множество косвенных подтверждений, полученных из сопоставления модели с конкретными особенностями раскраски шкуры у животных. Я убежден, что большинство существующих узоров раскраски может быть получено с помощью реакционно-диффузионной модели. Тем не менее тот факт, что многие общие и специфические черты раскраски шкуры у млекопитающих могут быть объяснены с помощью этой простой теории, еще не значит, что она правильна. Теорию могут подтвердить только экспериментальные наблюдения. Литература J.B.L. Bard. A unity underlying the different zebra striping patterns. // Journal of Zoology, Vol. 183, Part 4, pages 527-539; 1977. J.D. Murray. A pre-pattern formation mechanism for animal coat marking // Journal of Theoretical Biology, Vol. 88, No. I, pages 161-199; 1981. J.D. Murray. On pattern formation mechanisms for lepidopteran wing patterns and mammalian coat patterns. // Philosophical Transactions of the Royal Society of London, Series B, Vol. 295, No. 1078, pages 473-496; October 7, 1981. J.D. Murray and P.K. Maini. A new approach то the generation of pattern and form in embryology. // Science Progress Vol. 70, No. 280, Part 4, pages 539-553; 1986. Белинцев Б.Н. Диссипативные структуры и проблемы биологического формообразования. // Успехи физических наук, 1983, т. 141, вып. 1, с. 55-101. Марри Дж. Нелинейные дифференциальные уравнения. Лекция о моделях. - М.: Мир, 1983. Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическая биофизика. - М.: Наука, 1984. И. Эпстейн, К. Кастин, П. де Кеппер, М. Орбан. Колебательные химические реакции, "В мире науки", 1983, № 5, с. 72. Джеймс Д. Марри (James D. Murray) - профессор математической биологии и директор Центра математической биологии Оксфордского университета. Воспроизведено по журналу "В мире науки" (№ 5, 1988 г.)
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Отчего у леопарда пятна на шкуре // Дж. Д. Марри |
|
[time: 6 ms; queries: 7]
8 Мар 2026 04:35:51 GMT+3 |







 Генно-инженерные эксперименты показали, что количество пальцев у мышей зависит от двух взаимодействующих систем генов-регуляторов. По мере отключения этих генов пальцы становятся многочисленнее, короче и тоньше, а их концы соединяются костно-хрящевой дугой, так что в итоге кисть начинает напоминать плавник примитивной рыбы. Новые данные согласуются с гипотезой о том, что развитие пальцев основано на реакционно-диффузионном механизме самоорганизации, придуманном Аланом Тьюрингом в 1952 году.
Генно-инженерные эксперименты показали, что количество пальцев у мышей зависит от двух взаимодействующих систем генов-регуляторов. По мере отключения этих генов пальцы становятся многочисленнее, короче и тоньше, а их концы соединяются костно-хрящевой дугой, так что в итоге кисть начинает напоминать плавник примитивной рыбы. Новые данные согласуются с гипотезой о том, что развитие пальцев основано на реакционно-диффузионном механизме самоорганизации, придуманном Аланом Тьюрингом в 1952 году. В научных представлениях о происхождении жизни в последнее десятилетие происходит настоящая революция, и она далеко не завершена. К сожалению, эта информация доступна в основном только на английском языке. Цикл статей, предлагаемый вниманию читателей, отчасти восполнит этот пробел.
В научных представлениях о происхождении жизни в последнее десятилетие происходит настоящая революция, и она далеко не завершена. К сожалению, эта информация доступна в основном только на английском языке. Цикл статей, предлагаемый вниманию читателей, отчасти восполнит этот пробел. Продолжительность циклов большинства цикад не случайна, а представляет собой интервалы из простых чисел (чисел, делимых без остатка только на себя — 3, 5, 7, 11, 13, 17 и т. д.), являясь наиболее действенной стратегией выживания и размножения.
Продолжительность циклов большинства цикад не случайна, а представляет собой интервалы из простых чисел (чисел, делимых без остатка только на себя — 3, 5, 7, 11, 13, 17 и т. д.), являясь наиболее действенной стратегией выживания и размножения. Окраска многих животных устроена причудливо и замысловато. На клеточном уровне ее возникновение описывается реакционно-диффузными моделями при помощи систем дифференциальных уравнений. В недавней работе группа ученых из Швейцарии детально изучила механизм формирования окраски глазчатых ящериц Timon lepidus. Оказалось, что это происходит по правилам, характерным для дискретного клеточного автомата, где в роли ячеек автомата выступают отдельные чешуйки кожи ящериц. Математическое моделирование позволило понять, что реакционно-диффузная система может порождать клеточный автомат благодаря особым условиям — в данном случае это подходящие размеры чешуек и толщина кожи ящериц внутри и на границе чешуек.
Окраска многих животных устроена причудливо и замысловато. На клеточном уровне ее возникновение описывается реакционно-диффузными моделями при помощи систем дифференциальных уравнений. В недавней работе группа ученых из Швейцарии детально изучила механизм формирования окраски глазчатых ящериц Timon lepidus. Оказалось, что это происходит по правилам, характерным для дискретного клеточного автомата, где в роли ячеек автомата выступают отдельные чешуйки кожи ящериц. Математическое моделирование позволило понять, что реакционно-диффузная система может порождать клеточный автомат благодаря особым условиям — в данном случае это подходящие размеры чешуек и толщина кожи ящериц внутри и на границе чешуек. Закон квадрата — куба представляет собой следующий принцип: если объект пропорционально (то есть с помощью преобразования подобия) увеличивается (уменьшается) в размере, его новый объём будет пропорционален кубу масштабирующего коэффициента, а новая площадь его поверхности — пропорциональна квадрату масштабирующего коэффициент. Этот закон находит своё применение в технике и биомеханике.
Закон квадрата — куба представляет собой следующий принцип: если объект пропорционально (то есть с помощью преобразования подобия) увеличивается (уменьшается) в размере, его новый объём будет пропорционален кубу масштабирующего коэффициента, а новая площадь его поверхности — пропорциональна квадрату масштабирующего коэффициент. Этот закон находит своё применение в технике и биомеханике.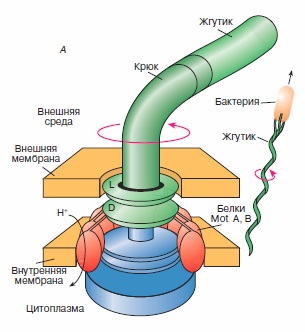 Рассмотрены строение и механизмы действия протонной АТРсинтазы и флагеллярного мотора - молекулярных моторов живой клетки, выполняющих химическую и механическую работу, связанную с их вращательным движением, строение и механизмы работы миозина и кинезина - механохимических белков, ответственных за сократительную активность и внутриклеточный транспорт органелл в клетке.
Рассмотрены строение и механизмы действия протонной АТРсинтазы и флагеллярного мотора - молекулярных моторов живой клетки, выполняющих химическую и механическую работу, связанную с их вращательным движением, строение и механизмы работы миозина и кинезина - механохимических белков, ответственных за сократительную активность и внутриклеточный транспорт органелл в клетке.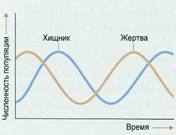 Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.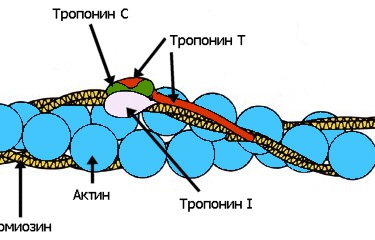 Почти всякая незыблемая общепринятая теория, которую с проклятьями зубрят школьники и которую устало и одинаково рассказывают учителя и даже профессора ВУЗов, при внимательном рассмотрении оказывается отнюдь не однозначной, захватывающей и полной загадок. К теории мышечного сокращения вышесказанное относится в полной мере. В общих чертах она была разработана еще в 50-х годах прошлого века, и классический рисунок с актиновыми и миозиновыми нитями до сих пор кочует из учебника в учебник. Однако реальная картина сокращения мышцы куда запутаннее, интереснее и непонятнее, со множеством подробностей и неожиданных действующих лиц и со сложными ролями, которые исполняют эти лица.
Почти всякая незыблемая общепринятая теория, которую с проклятьями зубрят школьники и которую устало и одинаково рассказывают учителя и даже профессора ВУЗов, при внимательном рассмотрении оказывается отнюдь не однозначной, захватывающей и полной загадок. К теории мышечного сокращения вышесказанное относится в полной мере. В общих чертах она была разработана еще в 50-х годах прошлого века, и классический рисунок с актиновыми и миозиновыми нитями до сих пор кочует из учебника в учебник. Однако реальная картина сокращения мышцы куда запутаннее, интереснее и непонятнее, со множеством подробностей и неожиданных действующих лиц и со сложными ролями, которые исполняют эти лица.