|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Теоремы софиста Горгия и современная математика // Дмитрий Фон-Дер-Флаасс |
Теоремы софиста Горгия и современная математикаДмитрий Фон-Дер-Флаасс
В июне этого года безвременно скончался Дмитрий Германович Фон-Дер-Флаасс (1962–2010), замечательный математик и педагог, светлый и обаятельный человек. Наши читатели не раз встречали это имя — журнал «Квант» часто публиковал его задачи. Дмитрий Германович успешно работал в большой науке, но это была лишь часть его деятельности. Вторую составляли математические олимпиады школьников: он работал в жюри Всесоюзных и Всероссийских олимпиад, а в последние годы — и Международных. Читал лекции в различных математических лагерях и школах, был одним из тренеров нашей команды на Международной математической олимпиаде. Мы предлагаем вашему вниманию запись (с небольшими сокращениями и с сохранением авторского стиля) лекции, прочитанной Дмитрием Фон-Дер-Флаассом во Всероссийском детском центре «Орленок» в 2009 году. Был такой античный софист Горгий. Знаменит он тем, что сформулировал три теоремы. Первая теорема звучит так: ничто в мире не существует. Вторая теорема: а ежели что и существует, то непознаваемо для человека. Третья теорема: а ежели все-таки что-то познаваемо, то непередаваемо ближнему. Другими словами, нет ничего, а ежели что-то есть, то мы об этом ничего не узнаем, а ежели даже что-то и узнаем, рассказать никому не сможем. Я добавил бы к этим трем теоремам еще четвертую: если даже мы и сможем что-то рассказать, то никто не заинтересуется. И вот эти четыре теоремы — это, собственно говоря, основные проблемы современной математики. Первая теорема ГоргияНачнем с первой — ничто в мире не существует, или, в переводе на язык математики, математика занимается непонятно чем. В некотором смысле это действительно так. Ведь математических объектов в мире не существует. Самое простое, с чего все начинается и чем математики все время пользуются, — это натуральные числа. Что такое натуральные числа, все мы знаем — это 1, 2, 3, 4 и так далее. И вот то, что мы все понимаем смысл слов «и так далее» — это большая загадка. Потому что «и так далее» означает, что чисел «бесконечно много». В нашем мире нет места для того, чтобы было бесконечно много чего-то. Но все мы уверены, что когда мы думаем о натуральных числах, мы все думаем об одном и том же. Если у меня после 7 следует 8, то и у вас после 7 будет следовать 8. Если у меня 19 — простое число, то у вас 19 будет простое число. Вот почему? Вроде бы в мире этого объекта нет, но мы о нем знаем и все знаем примерно одно и то же. Это, конечно, загадка не математическая, это загадка философская, и пусть философы ее обсуждают. Нам достаточно того, что, к счастью, мы все-таки имеем представление о математических объектах и оно одно и то же у всех, кто начинает о них задумываться. И поэтому математика возможна. Но большая философская проблема остается. Если, как это принято у математиков, задуматься об этом всерьез, т. е. попытаться как-то строго об этом подумать, то тогда возникают проблемы, о которых я сейчас расскажу. Возникли они на памяти человечества совсем недавно, буквально в последнюю сотню лет. Кроме натуральных чисел есть еще много чего в математике. Есть наша евклидова плоскость, на которой мы рисуем всякие треугольники, углы, доказываем о них теоремы. Есть действительные числа, есть комплексные числа, есть функции, есть еще что-то более страшное... Где-то на рубеже XIX–XX веков была проделана очень большая работа (хотя началась она, конечно, немного раньше), люди поняли, что все многообразие математических объектов в принципе можно свести к единому понятию — понятию множества. Конечно, если мы просто имеем интуитивное представление о том, что такое множество и что такое «и так далее», мы сможем построить в принципе всю математику. Что такое множество? Ну, это просто множество чего-то. Вопрос в том — что с множествами можно делать? Если у нас есть какое-то множество, то что означает, что оно у нас есть? Это означает, что про любой элемент нашего мира, мира математических объектов, мы можем спросить, а он в этом множестве лежит или не лежит, и получить ответ. Ответ однозначный, совершенно не зависящий от нашей воли. Вот это то первое, базовое, что можно с множествами делать, — узнавать, принадлежит элемент множеству или не принадлежит. Конечно, нужно еще сами эти множества как-то строить. Чтобы из них, в конце концов, построилось все богатство математических объектов. Как их можно строить? Можно, скажем, построить пустое множество: Ø. Самое первое, самое простое. Про него мы что знаем? Что про какой бы элемент мы ни спросили, принадлежит ли он этому множеству или нет, ответ всегда будет — нет, не принадлежит. И этим пустое множество уже однозначно определено. Все вопросы о нем получают мгновенный ответ. Ура! Теперь у нас уже есть вот это само пустое множество. И мы можем построить множество, которое ничего не содержит, кроме пустого множества: {Ø}. Опять же, что значит, что мы имеем это множество? Это значит, что про любой элемент мы можем спросить, он этому множеству принадлежит или нет. И если этот элемент — пустое множество, то ответ будет — «да». А если этот элемент любой другой, то ответ будет — «нет». Итак, это множество тоже задано. С этого все начинается. Можно использовать еще несколько интуитивных операций. Если у нас есть два множества, то мы можем их объединить. Можно сказать, что теперь будет множество, в котором будут элементы из того или из другого множества. Опять же, ответ на вопрос, принадлежит ли элемент полученному множеству или нет, однозначен. Значит, объединение мы можем построить. И так далее. В какой-то момент приходится отдельно объявить, что все-таки у нас есть какое-то множество, в котором элементов бесконечно много. Поскольку мы знаем, что натуральные числа есть, мы верим, что бесконечное множество существует. Объявляем, что множество натуральных чисел у нас тоже доступно. Как только появляется бесконечное множество, так дальше уже можно пуститься во все тяжкие и определять уже все что угодно. Можно определить целые числа. Целое число — это либо ноль, либо натуральное число, к которому приставлен или не приставлен знак минус. Все это, (может, и не так очевидно, как я говорю), можно проделать и на языке теории множеств. Можно определить рациональные числа. Что такое рациональное число? Это пара из двух чисел — числителя и (ненулевого) знаменателя. Нужно только определить, как их складывать, как их умножать между собой. И каковы условия, когда такие пары считать одним и тем же рациональным числом. Что такое действительное число? Вот интересный шаг. Вы можете сказать, например, что это бесконечная десятичная дробь. Вполне хорошее будет определение. А что это значит — бесконечная десятичная дробь? Это значит, у нас есть какая-то бесконечная последовательность цифр, т. е. просто для каждого натурального числа мы знаем, какая цифра стоит на этом месте нашего действительного числа. Все такие последовательности образуют действительные числа. Опять же, мы можем определить, как их складывать, как их умножать, и так далее.
Кстати, математики предпочитают определять действительные числа не так, а вот каким образом. Возьмем все рациональные числа — мы их уже имеем. А теперь объявим, что действительное число — это множество тех рациональных чисел, которые его строго меньше. Вот такое очень хитрое определение. На самом деле, оно очень похоже на предыдущее. Например, если у нас есть действительное число 3,1415926... (там дальше идет бесконечная цепочка цифр, которую я наизусть не знаю), то какие, например, будут рациональные числа, меньшие его? Обрежем дробь на втором знаке после запятой. Получим число 3,14, оно меньше нашего. Обрежем дробь на четвертом знаке после запятой — получим 3,1415, еще одно рациональное число, меньшее нашего. Ясно, что если мы знаем все рациональные числа, меньшие нашего числа, то это число единственным образом определено. Наглядно можно представить себе такую картинку, как на рисунке 1. Прямая — это все действительные числа, среди них где-то наше неизвестное, а слева от него много-много рациональных, которые его меньше. Все остальные рациональные будут, соответственно, его больше. Интуитивно понятно, что имеется единственная щелочка между этими двумя наборами рациональных чисел, и вот эту щелочку мы будем называть действительным числом. Это пример того, как, начиная с понятия множества, вся математика помаленьку раскручивается. Зачем это нужно? Понятно, что на практике, конечно, никто этим не пользуется. Когда математик изучает, скажем, функции комплексного переменного, он не вспоминает каждый раз, что комплексное число — это пара действительных, что действительное — это бесконечное множество рациональных, что рациональное — это пара целых и так далее. Он уже работает с вполне сформированными объектами. Но в принципе все можно расписать до самых основ. Будет очень длинно и не читаемо, но тем не менее это в принципе возможно. А дальше чем математики занимаются? Они доказывают разные свойства этих объектов. Чтобы что-то доказать, нужно уже что-то знать, какие-то первоначальные свойства всех этих объектов. И более того, математики должны быть полностью согласны насчет того, с каких первоначальных свойств начинать. Чтобы любой результат, полученный одним математиком, был принят всеми остальными.
Можно выписать несколько вот таких первоначальных свойств — они называются аксиомами, — и после этого из них доказывать все остальные свойства все более и более сложных математических объектов. Но вот уже с натуральными числами начинаются трудности. Аксиомы-то есть, и мы чувствуем интуитивно, что они верны, но оказывается, бывают такие утверждения про натуральные числа, которые из этих аксиом не выводятся, но которые, тем не менее, верны. Скажем, натуральные числа удовлетворяют некоторому свойству, но из тех аксиом, которые приняты за основные, оно получено быть не может. Сразу возникает вопрос, а откуда мы знаем тогда, что это свойство верно для натуральных чисел? Если мы его не можем вот так взять и доказать? Трудный вопрос. Получается примерно так. Если обходиться только аксиомами натуральных чисел, то об очень многих вещах в принципе даже невозможно и говорить. Например, невозможно говорить о произвольных бесконечных подмножествах натуральных чисел. Тем не менее, люди представляют себе, что это такое, и в принципе интуитивно понимают, какими свойствами эти подмножества определяются. Поэтому про некоторые свойства натуральных чисел, которые из аксиом не выводимы, люди могли знать, что они верны. И вот, математик Курт Гёдель, видимо, был первым, кто в явном виде показал некое свойство натуральных чисел, которое интуитивно верно (т. е. против того, что оно верно, математики не возражают), но при этом оно не выводимо из тех аксиом натуральных чисел, которые тогда были приняты. Частично, и на самом деле в очень большой степени (достаточной для большинства областей математики), с этой проблемой справились, аккуратно доведя все до множеств и выписав некоторый набор аксиом теории множеств, которые интуитивно очевидны и верность этих аксиом математиками, в общем-то, не оспаривается. Скажем, аксиома объединения. Если у нас есть набор каких-то множеств, то мы можем сказать: а давайте образуем множество, которое содержит все элементы вот этих множеств из этого набора. Нет никаких разумных возражений против того, что такое множество существует. Есть и более хитрые аксиомы, с которыми проблем немножко больше. Мы сейчас рассмотрим три хитрые аксиомы в теории множеств, про которые в принципе могут возникнуть сомнения.
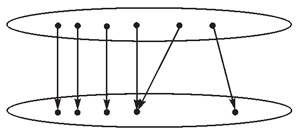
Например, есть такая аксиома. Допустим, что у нас есть множество каких-то элементов, и допустим, что по каждому из них мы можем однозначно определить значение некой функции на этом элементе. Аксиома говорит, что мы можем применить эту функцию к каждому элементу этого множества, и то, что получится, вместе снова будет образовывать множество (рис. 2). Самый простой пример: функция, переводящая x в x2, ее мы умеем считать. Скажем, если у нас есть какой-то набор натуральных чисел, то мы можем каждое из них возвести в квадрат. Получится снова какой-то набор натуральных чисел. Такая интуитивно очевидная аксиома, согласны? Но вот, проблема в том, что эти функции могут быть определены очень сложным образом, множества могут быть очень большими. Бывает и такая ситуация: про нашу функцию мы умеем доказывать, что она однозначно определена, но сосчитать конкретное значение этой функции для каждого элемента множества — это чрезвычайно трудно или даже бесконечно трудно. Хотя мы знаем, что какой-то ответ уж точно есть, причем он однозначен. Даже в таких сложных ситуациях эта аксиома считается по-прежнему применимой, и как раз вот в таком самом общем виде она служит одним из источников проблем в теории множеств.
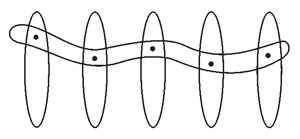
Вторая аксиома, которая, с одной стороны, очевидна, а с другой, приносит проблемы, — это аксиома взятия всех подмножеств данного множества. Она говорит, что если у нас какое-то множество есть, то у нас есть и множество, состоящее из всех подмножеств данного. Для конечных множеств это, разумеется, очевидно. Если у нас есть конечное множество из N элементов, то подмножеств у него будет всего 2N. В принципе мы их можем даже все выписать, если мы не очень ленивы. С самым простым бесконечным множеством, у нас проблем тоже нет. Смотрите: возьмем множество натуральных чисел 1, 2, 3, 4, 5, 6, 7 и так далее. Почему нам очевидно, что семейство всех подмножеств множества натуральных чисел существует? Потому что мы знаем, что это за элементы. Как можно представить себе подмножество натуральных чисел? Давайте поставим единички у тех элементов, которые мы берем, а нолики — у тех, которые не берем, ну и так далее. Можно представить себе, что это бесконечная двоичная дробь (рис. 3). С точностью до маленьких поправок (вроде того, что некоторые числа могут представляться двумя разными бесконечными двоичными дробями) оказывается, что действительные числа — это примерно то же самое, что подмножества натуральных чисел. И поскольку интуитивно мы знаем, что с действительными числами все в порядке, они есть, наглядно их можно представлять как непрерывную прямую, то в этом месте с нашей аксиомой о множестве всех подмножеств данного множества тоже все в порядке. Если дальше подумать, то становится уже немножко боязно. Тем не менее, математики считают, что эта аксиома всегда выполняется: если у нас какое-то множество есть, то значит, есть и множество всех его подмножеств. Иначе очень трудно было бы некоторые конструкции проделать. И еще одна аксиома, с которой было больше всего проблем, потому что в нее сначала не верили. Может быть, вы даже слышали ее название — аксиома выбора. Ее можно сформулировать многими разными способами, некоторыми — очень сложными, некоторыми — очень простыми. Я сейчас расскажу самый наглядный способ сформулировать аксиому выбора, при котором будет действительно очевидно, что она верна. Пусть у нас есть набор каких-то множеств. Они могут на самом деле быть и пересекающимися между собой, но это не важно — пусть для простоты они пока не пересекающиеся. Тогда мы можем построить произведение всех этих множеств. Что это означает? Элементами этого произведения будут вот такие штуки — мы из каждого возьмем по одному элементу и образуем из них всех одно множество (рис. 4). Каждый способ выбрать по одному элементу из множества дает элемент произведения этих множеств.
Конечно, если среди этих множеств оказалось пустое, из которого выбрать нечего, то произведение их всех тоже будет пусто. А аксиома выбора утверждает такой совершенно очевидный факт — если все эти множества не пустые, то и произведение будет непустое. Согласны, что факт очевиден? И это, видимо, послужило, в конце концов, одним из самых сильных аргументов в пользу того, что действительно аксиома выбора верна. В других формулировках аксиома выбора звучит совсем не так очевидно, как в этой. Наблюдения за тем, как математики доказывают свои утверждения, пытаясь перевести всю математику на язык теории множеств, показали, что во многих местах математики, сами того не замечая, эту аксиому используют. Как только это заметили, сразу стало понятно, что ее нужно выделить в отдельное утверждение — раз уж мы ее используем, то мы ее должны откуда-то взять. Либо мы должны ее доказать, либо мы должны объявить, что это базовый очевидный факт, который мы берем за аксиому и которым разрешаем пользоваться. Выяснилось, что это действительно базовый факт, что доказать его, используя только все остальные факты, невозможно, опровергнуть его тоже невозможно, и поэтому если уж его принимать, то принимать именно как аксиому. А принимать, конечно, надо, потому что в такой форме он и вправду очевиден. Тут и возникли большие проблемы, потому что как только этот факт в явном виде сформулировали и сказали «будем его использовать», математики тут же кинулись его использовать и, используя его, доказали большое количество совершенно интуитивно неочевидных утверждений. И даже, более того — утверждений, которые интуитивно кажутся неверными. Вот самый наглядный пример такого утверждения, которое доказали с помощью аксиомы выбора: можно взять шар, разделить его на несколько кусков и сложить из этих кусков два точно таких же шара. Что здесь означает «разделить на несколько кусков», допустим, на 7? Это значит, что про каждую точку мы говорим, в какой из этих семи кусков она попадает. Но это не то, что разрезать шар ножиком — это может быть гораздо сложнее. Например, вот такой трудно представимый, но легко объяснимый способ разрезать шар на два куска. Давайте возьмем в один кусок все точки, у которых все координаты рациональные, а в другой кусок — все точки, у которых есть иррациональная координата. Про каждую точку мы знаем, в какой из кусков она попала, т. е. это законное разделение шара на два куска. Но наглядно это представить себе очень трудно. Каждый из этих кусков, если издали на него посмотреть, будет выглядеть как шар целиком. Хотя один из этих кусков будет на самом деле очень маленький, а другой — очень большой. Так вот, доказали с помощью аксиомы выбора, что шар можно так разрезать на 7 кусков, а потом эти куски немножко передвинуть (именно передвинуть в пространстве, не искореживая никак, не искривляя) и собрать снова так, что получатся два шара, в точности таких же, как и тот, что был в самом начале. Это утверждение, хотя и доказано, звучит как-то дико. Но потом все-таки поняли, что лучше уж смириться с такими следствиями аксиомы выбора, чем вообще от нее отказываться. Иначе никак: либо мы отказываемся от аксиомы выбора, и тогда нам не удастся ее использовать вообще нигде, и очень многие важные красивые и интуитивно понятные математические результаты окажутся недоказуемыми. Либо мы ее берем — результаты становятся благополучно доказуемыми, но заодно у нас появляются такие вот уродцы. Но люди ко многому привыкают, и к этим уродцам они тоже привыкли. В общем, с аксиомой выбора сейчас вроде проблем нет. Получается так, что у нас есть набор аксиом для теории множеств, есть наша математика. И более-менее кажется, что все, что могут люди сделать в математике, может быть выражено на языке теории множеств. Но тут возникает та же самая проблема, которую в свое время обнаружил Гёдель в арифметике. Если у нас есть некий достаточно богатый набор аксиом, которые описывают наш мир множеств (который есть мир всей математики), обязательно найдутся утверждения, про которые мы никак не сможем узнать, верны они или нет. Утверждения, которые из этих аксиом доказать мы не сможем, и опровергнуть тоже не сможем. Теория множеств сильно развивается, и сейчас она ближе всего к этой проблеме: часто приходится сталкиваться с ситуацией, когда некоторые вопросы звучат вполне естественно, ответ на них получить хочется, но доказано, что ответа мы никогда не узнаем, потому что и тот ответ, и другой ответ из аксиом выведен быть не может. Что делать? В теории множеств как-то пытаются с этим бороться, а именно, пытаются придумывать новые аксиомы, которые по какой-то причине все-таки можно еще добавить. Хотя, казалось бы, все, что человечеству интуитивно очевидно, уже сведено к тем аксиомам теории множеств, которые были выработаны в начале XX века. А теперь оказывается, что хочется все-таки еще чего-то. Математики тренируют свою интуицию дальше, чтобы какие-то новые утверждения вдруг показались почему-то всем математикам интуитивно очевидными, и тогда их можно было бы принять в качестве новых аксиом в надежде, что с их помощью ответы на какие-то из таких вопросов могут быть получены. О том, как все это происходит, конечно, рассказать я не могу, там чрезвычайно сложные утверждения, и нужно очень глубоко вкопаться в теорию множеств, во-первых, для того, чтобы понять, что они утверждают, а во-вторых, чтобы понять, что эти утверждения действительно можно считать интуитивно очевидными и принять за аксиомы. Вот этим занимается сейчас одна из самых загадочных областей математики — теория множеств. Вторая теорема ГоргияВторая теорема Горгия звучит так — если что и существует, то непознаваемо для человека. Сейчас я покажу несколько примеров утверждений, которые под эту категорию попадают. С теорией множеств была проблема, имеем ли мы вообще право задавать вопросы вроде такого: «верна ли аксиома выбора?». Если мы хотим просто заниматься математикой, не вступая в противоречия, то мы в принципе можем и принять аксиому выбора, и принять, что она не верна. И в том и в другом случае мы сможем развивать математику, получая одни результаты в одном случае, другие — в другом, но никогда не придем к противоречию. А вот теперь другая ситуация. Есть, видимо, результаты, ответ на которые очевидно существует, и очевидно он однозначно определен, но человечество его, может быть, никогда не узнает. Самый простой пример — это так называемая (3N + 1)-проблема, о которой я сейчас расскажу. Возьмем любое натуральное число. Если оно четно, то разделим его пополам. А если оно нечетно, то умножим его на 3 и прибавим 1. С полученным числом проделаем то же самое, и так далее. Например, если мы начнем с тройки, получится
Если мы начнем с семерки, немножко дольше будет продолжаться процесс. Уже начиная с некоторых маленьких чисел, эта цепочка может оказаться достаточно длинной, но все время она будет заканчиваться единичкой. Есть гипотеза, что с какого бы числа мы ни начали, если мы будем такую цепочку строить, то всегда обязательно доберемся до 1. В этом и состоит (3N + 1)-проблема — верна ли эта гипотеза? Мне кажется, что все нынешние математики верят, что она верна. И некоторые самые безрассудные даже пытаются ее доказать. Но ни у кого ничего не вышло. И не выходит уже много десятков лет. Так что это одна из привлекательных задач. Серьезные математики, конечно, относятся к ней свысока — просто как к забавной головоломке. Неизвестно, что там будет, да и кому нужно знать, что там будет. Но несерьезным математикам все-таки интересно, справедлива гипотеза или нет. И пока ее не доказали, совершенно все что угодно тут может произойти. Во-первых, очевидно, что у этого вопроса ответ однозначный: да или нет. Либо правда, что, начиная от любого натурального числа, мы сползем к единице, либо неправда. Интуитивно ясно, что тут уже ни от какого выбора аксиом, ни от какой воли человеческой ответ не зависит. Так вот, есть предположение, что человечество никогда не узнает ответ на этот вопрос.
Конечно, если кто-то докажет эту гипотезу, то тогда мы узнаем ответ. Но что значит докажет? Это значит, что он объяснит нам, по каким причинам любое натуральное число сходится к 1, и эти причины окажутся для нас понятными. Может случиться, что кто-то докажет, что некоторое семидесятитрехзначное число обладает именно такими свойствами, что запустив от него эту цепочку, мы обязательно будем получать сколь угодно большие числа. Или докажет, что эта цепочка зациклится где-то в другом месте. Опять же, это будет причиной, почему гипотеза неверна. А вот у меня, например, такой страшный кошмар: а что, если это утверждение верно, но без всякой на то причины? Верно, а причины, которую один человек может понять и объяснить другому, у этого утверждения нет вовсе. Тогда мы никогда не узнаем ответа. Потому что останется только перебрать все натуральные числа и для каждого проверить гипотезу. А это, естественно, вне наших сил. Закон сохранения энергии не позволяет проделать бесконечное количество операций за конечное время. Или конечность скорости света. В общем, физические законы не позволяют нам проделать бесконечное количество операций за конечное время и узнать результат. Очень многие нерешенные задачи как раз относятся именно к этой области, т. е. в принципе их очень хотят решить. Некоторые из них скорее всего решат. Вы все наверняка слышали название «гипотеза Римана». Может быть кто-нибудь из вас даже смутно понимает, что эта гипотеза гласит. Я лично понимаю очень смутно. Но с гипотезой Римана, по крайней мере, более менее ясно, что она верна. Все математики в нее верят, и, я надеюсь, ее докажут в ближайшее время. А есть некоторые утверждения, которые никто не может пока ни доказать, ни опровергнуть, и даже в гипотезе нет уверенности, какой из двух ответов верен. Возможно, что на какие-нибудь из этих вопросов человечество в принципе никогда ответов не получит. Третья теорема ГоргияТретья теорема — ежели что-то и познаваемо, то непередаваемо ближнему. Тут как раз самые жгучие проблемы у современной математики и самые, может быть, муссируемые. Человек что-то доказал, но рассказать это доказательство другому человеку он не способен. Или убедить другого человека в том, что он действительно это доказал. Так бывает. Самый первый пример из этой области и самый известный публике -это проблема четырех красок. Но это еще не самая тяжелая ситуация, которая здесь возникает. Я сейчас скажу немножко про проблему четырех красок, а потом покажу ситуации более безумные.
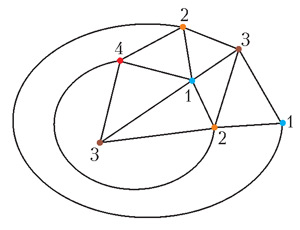
Что такое проблема четырех красок? Это вопрос из теории графов. Граф — это просто некоторые вершины, которые могут быть соединены между собой ребрами. Если мы эти вершины сможем нарисовать на плоскости, и ребрами соединить так, чтобы ребра между собой не пересекались, получится граф, который называется плоским. Что такое раскраска графа? Мы красим его вершины в разные цвета. Если мы это сделали так, что соседние по ребру вершины всегда разного цвета, раскраска называется правильной. Хочется правильно покрасить граф, использовав как можно меньше различных цветов. Вот, например, на рисунке 5 у нас есть три вершины, которые попарно соединены — значит, никуда не денешься, эти вершины будут обязательно иметь три разных цвета. Но вообще для покраски этого графа хватает четырех цветов (а трех не хватает, можете проверить). Сто лет стояла проблема: правда ли, что любой граф, который можно нарисовать на плоскости, можно раскрасить в четыре цвета? Кто-то верил и пытался доказать, что четырех цветов всегда хватит, кто-то не верил и пытался придумать пример, когда четырех цветов не хватит. Еще была такая неприятность: проблема очень легко формулируется. Поэтому многие люди, даже несерьезные математики, накинулись на нее и стали пытаться ее доказывать. И предъявляли огромное количество якобы доказательств или якобы опровержений. Посылали их математикам, кричали в газетах: «Ура! Я доказал проблему четырех красок!» — и даже выпускали книжки с ошибочными доказательствами. Словом, большой был шум. В конце концов ее доказали К. Аппель и В. Хакен. Схему доказательства я вам сейчас примерно опишу. И заодно мы увидим, почему это доказательство непередаваемо другим. Начали люди с того, что всерьез стали изучать, как устроены плоские графы. Они предъявили список из нескольких десятков конфигураций и доказали, что в каждом плоском графе какая-то из этих конфигураций обязательно найдется. Это первая половина доказательства. А вторая половина доказательства — для каждой из этих конфигураций можно проверить, что если она в нашем графе есть, то его удастся раскрасить в четыре цвета. Более точно, дальше доказательство идет от противного. Предположим, что наш граф нельзя раскрасить в четыре цвета. Из первой половины мы знаем, что в нем есть какая-то конфигурация из списка. После этого для каждой из этих конфигураций проводится такое рассуждение. Предположим, что наш граф содержит эту конфигурацию. Выкинем ее. По индукции, то, что осталось, в четыре цвета красится. И проверяем, что как бы мы ни раскрасили оставшееся в четыре цвета, вот эту саму конфигурацию докрасить нам удастся. Самый простой пример докрашиваемой конфигурации — вершина, которая соединена всего с тремя другими. Понятно, что если в нашем графе есть такая вершина, то мы можем оставить раскрашивание ее напоследок. Раскрасим все остальное, а потом посмотрим, к каким цветам присоединена эта вершина, и выберем четвертый. Для других конфигураций рассуждения аналогичные, но более сложные. Теперь, как все это было проделано? Проверить, что каждая из такого большого количества конфигураций всегда докрашивается, руками невозможно — надо слишком много времени. И вот эту проверку поручили компьютеру. А он, перебрав большое количество случаев, действительно проверил, что это так. В результате появилось доказательство проблемы четырех красок. Первоначально выглядело оно вот как. Человеческая часть рассуждения, записанная в толстой книге, и к ней прилагались фразы, что окончательная проверка того, что все раскрашивается, была поручена компьютеру, и даже текст компьютерной программы приводился. Эта программа все просчитала и все проверила — действительно, все нормально, и значит, теорема четырех красок доказана. Тут же поднялся шум — можно ли такому доказательству верить. Ведь большая часть доказательства проведена компьютером, а не человеком. «А вдруг компьютер ошибся?» — говорили такие недалекие люди. И проблемы с этим доказательством действительно начались, но они оказались не в компьютерной части, а в человеческой. В доказательстве были найдены недочеты. Понятно, что такой длины текст, содержащий сложные переборы, конечно, может содержать ошибки. Ошибки эти были найдены, но, к счастью, их удалось исправить.
Осталась компьютерная часть, которую с тех пор уже тоже проверили не на одном компьютере, переписывая даже программы, просто проделав тот же перебор. Ведь если сказано, что именно следует перебирать, то каждый может написать свою программу и проверить, что результат будет такой, как надо. И мне, например, кажется, что использование таких вот больших компьютерных переборов в доказательстве — это как раз не проблема. Почему? А вот по той же причине, которая на примере проблемы четырех красок уже проявилась — что к компьютерным доказательствам доверия гораздо больше, чем к человеческим, а не меньше. Кричали, что компьютер — это же машина, а вдруг она где-то сломалась, сбилась, что-то там неправильно посчитала... А вот этого как раз быть не может. Потому что если компьютер случайно где-то засбоил, и произошла ошибка — нолик случайно заменился на единичку, — это не приведет к неверному результату. Это приведет к отсутствию результата, просто программа в конце концов сломается. Какая типичная операция, которую компьютер выполняет? Взяли из такого-то регистра такое-то число и передали по нему управление туда-то. Естественно, что если в этом числе произошло изменение в один бит, управление передалось вообще неизвестно куда, там написаны какие-то команды, которые очень скоро просто все разрушат. Может быть, конечно, ошибка в написании программы для компьютера, но это уже человеческая ошибка. Человек может прочитать программу и проверить, правильная она или нет. Так же человек может прочитать чужое доказательство и проверить, правильное оно или нет. Но у человека гораздо больше шансов ошибиться, чем у компьютера. Если вы читаете чужое достаточно длинное доказательство, и в нем есть ошибка, то есть все шансы, что вы ее не заметите. Почему? В первую очередь потому, что раз сам автор доказательства сделал эту ошибку — значит, она психологически обоснована. То есть, он не просто так ее сделал, по случайности — это в принципе такое место, где типичный человек может сделать такую ошибку. Значит, и вы можете сделать ту же самую ошибку, читая это место и соответственно ее не заметив. Поэтому проверка человеком, человеческого же доказательства — это гораздо менее надежный способ проверки, чем проверка результата работы компьютерной программы с помощью запуска ее еще раз на какой-то другой машине. Второе практически гарантирует, что все нормально, а первое — это как повезло. И вот с этой проблемой — найти ошибку в записанном людьми математическом тексте, — становится все труднее, а иногда и вообще невозможно — это серьезная проблема современной математики. С ней нужно бороться. Как — сейчас пока никто не знает. А проблема большая и всерьез возникла именно сейчас — тому несколько примеров существует. Вот, возможно, менее известный, но один из самых современных. Это старинная гипотеза Кеплера. Говорит она об укладывании шариков в трехмерном пространстве.
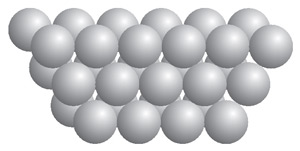
Давайте сначала посмотрим, что происходит в двумерном пространстве, т. е. на плоскости. Пусть у нас есть одинаковые кружочки. Как плотнее всего нарисовать их на плоскости, чтобы они не пересекались? Есть ответ — надо поместить центры кружков в узлы шестиугольной решетки. Это утверждение не совсем тривиальное, но легкое. А в трехмерном пространстве как бы вы стали плотно упаковывать шарики? Сначала разложим на плоскости шарики так, как показано на рисунке 6. Потом сверху положим еще один такой же слой, вдавливая до упора, как показано на рисунке 7. Потом сверху еще один такой же слой, и так далее. Интуитивно очевидно, что это и есть самый плотный способ уложить шарики в трехмерном пространстве. Кеплер утверждал (и, похоже, первым сформулировал), что эта упаковка должна быть самой плотной упаковкой в трехмерном пространстве. Произошло это в XVII веке, с тех пор эта гипотеза и стоит. В начале XXI века появилось ее доказательство. И любой из вас может его достать и прочитать. Оно в открытом доступе лежит в Интернете. Это статья в двести с чем-то страниц. Она написана каким-то одним человеком, и тоже содержит как некоторые чисто математические рассуждения, так и компьютерный счет.
Сначала автор математическими рассуждениями пытается свести задачу к проверке конечного числа случаев. После этого, иногда используя компьютер, он это конечное, но очень большое число случаев проверяет, все сходится, и — ура! — гипотеза Кеплера доказана. И вот проблема с этой статьей — ее никто не может прочитать. Потому что она тяжелая, потому что местами не совсем понятно, что перебор действительно полный, потому что просто скучно ее читать. Двести страниц скучных вычислений. Человек ее прочитать не в силах. Вообще говоря, все верят, что эта статья содержит доказательство этой теоремы. Но с другой стороны, никто до сих пор не проверил это честно, в частности, эта статья не опубликована ни в одном рецензируемом журнале, т. е. никакой уважающий себя математик не готов поставить подпись под утверждением, что «да, все верно, и гипотеза Кеплера доказана». И это не единственная ситуация, и в других областях математики такое тоже встречается. Совсем недавно я напоролся на список нерешенных проблем в теории множеств, в теории моделей, в разных областях. И вот к одной гипотезе там комментарии такие: она якобы опровергнута в статье вот такой-то, но никто в это не верит. Вот такая ситуация. Человек доказал утверждение, но передать это другому, рассказать это другому он не в силах. Самый страшный пример — это, конечно, классификация конечных простых групп. Я не буду формулировать точно, что это такое, что такое группы, что такое конечные группы, если захотите — узнаете сами. Конечные группы все в некотором смысле собираются из простых блоков, которые называются простыми группами, а те уже нельзя разобрать на более мелкие блоки. Этих конечных простых групп бесконечно много. Полный их список выглядит так: это семнадцать бесконечных серий, к которым еще в конце добавлены 26 отдельных групп, которые построены каким-то отдельным способом и ни в какую серию не входят. Утверждается, что этот список содержит все конечные простые группы. Задача страшно нужная для математики. Поэтому в 70-е годы, когда появились некоторые особенные идеи и надежды на ее решение, на задачу накинулись несколько сот математиков из разных стран, из разных институтов, каждый брался за свой кусочек. Были и, так сказать, архитекторы этого проекта, которые примерно представляли, как все это вместе потом будет собрано в единое доказательство. Понятно, что люди торопились, конкурировали. В результате, кусочки, которые они делали — это в совокупности около 10000 журнальных страниц, и это только то, что опубликовано. А есть еще и статьи, которые существовали или в виде препринтов, или в виде машинописных копий. Я сам одну такую статью читал в свое время, она так никогда и не была опубликована, хотя включает в себя заметный кусочек этого полного доказательства. И вот эти 10000 страниц разбросаны в разных журналах, написаны разными людьми, с разной степенью понятности, и обычному математику, не связанному с этим и не являющемуся одним из архитекторов этой теории, мало того что невозможно прочитать все 10000 страниц, так еще и очень трудно понять само устройство доказательства. К тому же с тех пор некоторые из этих архитекторов просто умерли. Объявили, что классификация завершена, хоть доказательство и существует лишь в виде текста, который никто прочитать не может, и это привело к следующей неприятности. Новые математики с меньшей охотой стали идти в теорию конечных групп. Все меньше и меньше людей этим занимается. И вполне может случиться, что через 50 лет уже вообще на Земле не найдется человека, который будет способен что-то понять в этом доказательстве. Будут ходить легенды: наши великие предки умели доказывать, что все конечные простые группы перечислены вот в этом списке, и что других нет, но сейчас это знание утеряно. Вполне реалистичная ситуация. Но, к счастью, не один я считаю эту ситуацию реалистичной, поэтому с ней борются, и я слышал, что даже организовали специальный проект «Философские и математические проблемы, связанные с доказательством классификации конечных простых групп». Есть люди, которые пытаются это доказательство привести к читаемому виду, и, может быть, когда-нибудь это действительно получится. Есть люди, которые пытаются разобраться, что же делать со всеми этими трудностями. Человечество помнит об этой задаче, и, значит, оно с ней, в конце концов справится. Но тем не менее вполне может быть, что будут появляться другие такие же сложные теоремы, которые могут быть доказаны, но доказательство которых никто не способен прочитать, никто не способен никому рассказать. Четвертая теоремаНу и теперь четвертая теорема, о которой я немного расскажу, может быть даже самая страшная — «ежели даже и сможет рассказать, то никто не заинтересуется». Некий осколок от этой проблемы уже прозвучал. Людям перестало интересно заниматься конечными группами. Все меньше и меньше людей этим занимаются, и масса знаний, которая сохранилась в виде текстов, уже никому не нужна, ее никто не умеет читать. Это тоже беда, которая грозит многим областям математики. Понятно, что некоторым областям математики везет. Например, та же самая теория графов и комбинаторика. Чтобы серьезно начать ими заниматься, нужно знать совсем немного. Вы немножко узнали, порешали олимпиадные задачки, один шаг — и перед вами уже нерешенная проблема. Есть за что взяться — ура, беремся, интересно, занимаемся. Но есть области математики, в которых даже для того, чтобы почувствовать, что эта область действительно красива, и что ей хочется заниматься, нужно очень многое узнать. И при этом по дороге еще много другого красивого узнаешь. Но тебя не должны эти красоты, встреченные по дороге, отвлечь, и в конце концов ты добираешься вот туда, в самые дебри, уже там видишь красоту, и уже тогда, узнав очень многое, становишься способен заниматься этой областью математики. И вот эта трудность — проблема для таких областей. Чтобы область математики развивалась, нужно, чтобы ею занимались. Достаточному числу людей это должно быть настолько интересно, чтобы они преодолели все трудности, забрались туда и уже после этого продолжили этим заниматься. И сейчас математика доходит до такого уровня сложности, что для многих областей именно это становится основной проблемой. Как человечество со всеми этими проблемами будет справляться — я не знаю, но посмотреть будет интересно. Вот, собственно, и все. «Квант» №5, 2010
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Теоремы софиста Горгия и современная математика // Дмитрий Фон-Дер-Флаасс |
|
[time: 8 ms; queries: 7]
11 Мар 2026 02:49:21 GMT+3 |





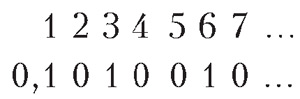
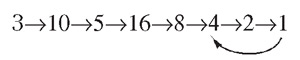



 В этой книге говориться о математике как о части культуры духовной. Данный текст писался не для математиков, а скорее для гуманитариев. Поэтому при его составлении в ряде случаев приходилось выбирать между понятностью и точностью. Предпочтение отдавалось понятности. Очерчивая место математики в современной культуре, автор пытается прояснить для читателей-нематематиков некоторые основные понятия и проблемы «царицы наук».
В этой книге говориться о математике как о части культуры духовной. Данный текст писался не для математиков, а скорее для гуманитариев. Поэтому при его составлении в ряде случаев приходилось выбирать между понятностью и точностью. Предпочтение отдавалось понятности. Очерчивая место математики в современной культуре, автор пытается прояснить для читателей-нематематиков некоторые основные понятия и проблемы «царицы наук». Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов. Если в качестве значений переменных разрешается брать только элементы носителя, язык называют элементарным языком, или языком первого порядка. Если же в качестве значений переменных разрешается брать также функции и отношения, язык называют языком второго порядка. Выразительные возможности языков первого порядка довольно ограничены. Например, на языке первого порядка можно сообщить, что носитель содержит ровно 17 элементов, но невозможно выразить его конечность. На языке второго порядка выразить конечность носителя возможно. Возникает совершенно естественное недоумение: а зачем тогда пользоваться языками первого порядка с их бедными выразительными средствами, не лучше ли пользоваться языками второго порядка?
Если в качестве значений переменных разрешается брать только элементы носителя, язык называют элементарным языком, или языком первого порядка. Если же в качестве значений переменных разрешается брать также функции и отношения, язык называют языком второго порядка. Выразительные возможности языков первого порядка довольно ограничены. Например, на языке первого порядка можно сообщить, что носитель содержит ровно 17 элементов, но невозможно выразить его конечность. На языке второго порядка выразить конечность носителя возможно. Возникает совершенно естественное недоумение: а зачем тогда пользоваться языками первого порядка с их бедными выразительными средствами, не лучше ли пользоваться языками второго порядка? Всякая надежда на создание единой математической теории, амбициозного проекта, который был предложен математиком Давидом Гильбертом в 19 веке и продолжил существовать, поддерживаемый многими, в 20 столетии, рухнула. Основы математики были далеко не столь надежными, как того хотел бы Гильберт. А Гëдель своими теоремами ясно продемонстрировал, что любая система аксиом, какой бы обширной она ни была, уязвима для возникновения невосполнимых пробелов. Попытки же восполнить их созданием более полной системы породили бы только бóльшее количество утверждений без доказательств — так что и тут возникнет необходимость в усовершенствовании системы, и так далее до бесконечности. И случилось нечто странное: математики решили не обращать на это внимания. Они посчитали, что неполнота систем не имеет непосредственного влияния на их работу.
Всякая надежда на создание единой математической теории, амбициозного проекта, который был предложен математиком Давидом Гильбертом в 19 веке и продолжил существовать, поддерживаемый многими, в 20 столетии, рухнула. Основы математики были далеко не столь надежными, как того хотел бы Гильберт. А Гëдель своими теоремами ясно продемонстрировал, что любая система аксиом, какой бы обширной она ни была, уязвима для возникновения невосполнимых пробелов. Попытки же восполнить их созданием более полной системы породили бы только бóльшее количество утверждений без доказательств — так что и тут возникнет необходимость в усовершенствовании системы, и так далее до бесконечности. И случилось нечто странное: математики решили не обращать на это внимания. Они посчитали, что неполнота систем не имеет непосредственного влияния на их работу.