|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Софи Жермен // Эми Дайан-Дальмедико |
Софи ЖерменЭми Дайан-Дальмедико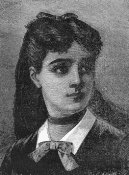
Преодолевая предрассудки французского общества XIX века, она стала выдающимся математиком и добилась важных результатов в теории чисел и теории упругости.
Сможете ли вы назвать хоть одного прославленного математика-женщину? Берусь поспорить, что не сможете. [Эта статья была написана для французской версии журнала «Scientific American». В России, хочется надеяться, вспомнят хотя бы Софью Ковалевскую. — редактор сайта ega-math.narod.ru] Прежде всего вам следовало бы вспомнить об Ипатии Александрийской. Современники похвально отзывались о её математических работах, хотя ни одна из них не сохранилась до наших дней. Возможно, её сочинения были уничтожены монахами–христианами, которые забили её камнями в 415 году за то, что она была язычницей. Приблизительно через 13 столетий была маркиза де Шатле, которая перевела на французский язык «Математические принципы» Исаака Ньютона. В 1750 году итальянка Мария Гаэтана Аньези, известная своими достижениями в дифференциальном исчислении, стала первой женщиной, получившей звание профессора математики.
Так же как Ипатии, маркизе де Шатле и М. Аньези, Софи Жермен пришлось выдержать ожесточённую борьбу с предрассудками семьи, друзей и коллег, прежде чем она стала настоящим математиком. Жермен обладала выдающимися способностями, неуёмным честолюбием и была страстно увлечена математикой. Она самостоятельно изучила математику и физику и стала автором оригинальных работ в теории чисел и теории упругости. Несмотря на эти достижения, Жермен так и не получила заслуженного признания. Софи Жермен родилась в Париже 1 апреля 1776 года, за 10 лет до Французской революции и спустя столетие после Научной революции. Законы Ньютона управляли Вселенной, в то время как указы Людовика XVI правили Францией. Жермен поддерживала политические перемены, служила прогрессу математики и физики и решительно боролась с барьерами, преграждавшими женщинам путь к научной деятельности. Её отец, Амбруаз-Франсуа Жермен был всецело поглощён Французской революцией. Он принадлежал к прослойке либеральной образованной буржуазии. Род Жермен из поколения в поколение занимался торговлей, и семья имела достаточное состояние. Защищая интересы своего сословия, Амбруаз являлся депутатом Ассамблеи, куда он был избран в 1789 году. В возрасте 13 лет Софи, по свидетельству знакомых, была робким, угловатым подростком. Считая, что её семья помешана на деньгах и политике, она находила убежище в отцовской библиотеке. Там и началось её интеллектуальное развитие. Софи изучила математику, прочтя все книги, которые ей удалось найти. Так же как она не могла понять интереса своих родителей к политике, они не понимали её увлечения математикой, считая её интересы удивительными для её возраста и несовместимыми с её полом. Итальянский математик Дж. Т. Либри-Каруччи (позже ставший другом Софи) рассказывал, как Софи преодолевала настоятельное желание родителей, чтобы она бросила увлечение математикой. Когда все в доме ложились спать, она занималась при свечах. Зимними ночами, когда чернила замерзали в чернильнице, она читала, завернувшись в одеяла. Её решимость оказалась сильнее родительской воли. И несмотря на её «странные» интересы, отец оказывал ей материальную поддержку на протяжении всей жизни. Софи не вышла замуж и не добилась профессионального положения, которое дало бы ей средства к существованию. Софи Жермен очень любила читать об Архимеде в «Истории математики» Жана Этьена Монтукла. Мысленно она отождествляла себя с Архимедом, боровшимся за продолжение своих исследований во время нападения римлян на Сиракузы. Она совершенствовала свои знания, продвигаясь от трактата Этьена Безу о математике к работам Ньютона и швейцарского математика Леонарда Эйлера. Родственники, друзья и наставники мало внимания обращали на интересы и способности юной Софи. Они не видели смысла в том, чтобы всерьёз заниматься развитием интеллектуальных способностей молодой женщины из семьи среднего класса.
Жермен было 19 лет, когда была основана Политехническая школа. Она доставала конспекты лекций по многим курсам, включая анализ, который читал Жозеф Луи Лагранж, и химию, которую читал Антуан Франсуа Фуркруа. На одном из занятий Лагранж попросил студентов изложить письменно своё мнение о прочитанном им курсе. Опасаясь, что её сочинение не станут читать, Жермен представила свою работу под именем бывшего студента Антуана Огюста Леблана. (Кстати, не известно, давал ли на это своё согласие Леблан.) Научное образование Жермен было в высшей степени необычным для женщины её класса. В XVIII веке наука преподавалась некоторым женщинам из аристократических кругов в популяризированном изложении, по учебникам, написанным специально для этой цели. О науке в них говорилось ровно столько, сколько было достаточно, чтобы женщина могла поддержать «учёный разговор» в аристократических салонах. Одну из самых примечательных книг в этом жанре «Философия сэра Исаака Ньютона в изложении для дам» написал Франческо Альгаротти. Альгаротти считал, что женщин интересует лишь рыцарская романтика и любовь, и поэтому он преподавал физику с учётом этого обстоятельства. Его книга построена на диалоге между некоей маркизой и её собеседником. В одной из сцен собеседник объясняет закон об обратной квадратичной зависимости. Он говорит, что сила взаимного притяжения или интенсивность света, например, убывает пропорционально квадрату расстояния между объектом и наблюдателем. Маркиза отвечает, что ей знакомо это понятие: «У меня невольно возникает ассоциация... мне кажется, что эта обратная квадратичная зависимость... наблюдается даже в любви. Скажем, после восьми дней разлуки любовь становится в шестьдесят четыре раза слабее, чем в первый день». Книга полна примерами подобного рода, среди которых приведённые в ней немногие строгие физические объяснения буквально теряются. Жермен терпеть не могла такой фривольной литературы. Жозеф-Жером Лаланд однажды привел её в ярость, намекнув, что она не сможет понять работу Пьера Симона Лапласа, если предварительно не прочитает книгу Лаланда «Астрономия для женщин». Жермен публично объявила, что никогда более не будет разговаривать с Лаландом. Её образование было бессистемным и непоследовательным. Она была удостоена встречи с Лагранжем и несколькими другими учёными. Некоторые из них предложили её вниманию небольшие задачи. Однако Жермен стремилась к тому, чтобы получить профессиональную подготовку, но такая возможность ей так и не представилась. Жермен была изолирована не только от общества учёных мужей, но и от других образованных женщин. Её социальное положение не позволяло ей общаться с женщинами из аристократических кругов. Кроме того, у неё не было родственников или близких знакомых среди образованных мужчин, которые могли бы представлять её идеи в научном мире; именно такие связи благоприятствовали, в частности, графине Готта и мадам Лаланд. Возможно, Жермен и сама в какой-то степени способствовала своей изоляции. По своей природной скромности и застенчивости она избегала светской жизни. Подобно великим энциклопедистам, сочинения которых её занимали, она полагала, что её научные работы сами по себе принесут ей непреходящее признание наперекор предрассудкам общества. Жермен оказалась в стороне от научного сообщества в тот период, когда оно привлекало к себе всё большее число людей, организовывало всё больше научных учреждений и как никогда прежде способствовало сотрудничеству между учёными. Она уже не занималась в холодной спальне, но с радостью преодолела бы ледяную стену, чтобы её работа получила какое-то признание. На рубеже XVIII и XIX веков Жермен предоставилась хорошая возможность проявить свои способности в области теории чисел. Первые профессионалы, с которыми она познакомилась, Лагранж и Адриен Мари Лежандр, оба очень интересовались этим предметом и поощряли её занятия. Через несколько лет она уже хорошо разбиралась в сложных методах, изложенных в «Арифметических исследованиях» немецкого математика Карла Фридриха Гаусса. Находясь под сильным впечатлением от книги, Жермен послала её автору около десятка писем в период между 1804 и 1809 годами. Свои письма она подписывала псевдонимом «Леблан», поскольку боялась «насмешек по поводу женщины-учёного». Друзья и соперники Софи Жермен были в числе наиболее знаменитых математиков и физиков XIX века, но большинство учёных относились к ней с безразличием. В начале своей научной карьеры Жермен переписывалась с Карлом Фридрихом Гауссом по вопросам теории чисел. Жозеф Луи Лагранж поощрял её в изучении математики и физики. Примерно в 1814 году она соревновалась с Симеоном Дени Пуассоном, пытаясь построить теорию упругости. В конце своей жизни она сотрудничала и дружила с Жаном Батистом Жозефом Фурье. В своём первом письме Гауссу Жермен обсуждает уравнение Ферма где Жермен открыла, что уравнение Ферма не имеет решения, когда Гаусс ответил: «Я в восторге от того, что арифметика нашла в вашем лице такого способного друга. Ваше новое доказательство... весьма изящно, хотя охватывает, по-видимому, довольно частный случай и не может быть применено к другим числам». В 1806 году Жермен послала письмо Гауссу с Жозефом-Мари Пернети, армейским офицером, который был её приятелем. Жермен беспокоилась о безопасности Гаусса, так как незадолго до этого Наполеон овладел большей частью Пруссии. Она сказала Пернети, что боится, как бы Гаусса не постигла та же судьба, что и Архимеда, который был убит римлянами. Пернети велел передать с посыльным, что Гаусс жив, здоров, но что математик не знает, кто такая Софи Жермен. В своём следующем письме Гауссу Жермен (она же Леблан) открывает своё подлинное имя. Гаусс был весьма удивлён и обрадован. «Женщина из-за своего пола и наших предрассудков встречается со значительно более трудными препятствиями, чем мужчина, постигая сложные научные проблемы. Но когда она преодолевает эти барьеры и проникает в тайны мироздания, она несомненно проявляет благородную смелость, исключительный талант и высшую гениальность». В своих похвалах в адрес Жермен Гаусс был искренен. Это, в частности, подтверждается в его письмах немецкому астроному Генриху Ольберсу. В 1808 году Жермен пишет новое письмо Гауссу, говоря в нём о том, что станет наиболее блестящей её работой в теории чисел. Жермен доказала, что если то либо Гаусс так никогда и не высказал своего мнения по поводу теоремы Жермен. Как раз перед этим он стал профессором астрономии в Гёттингенском университете и вынужден был отложить свои исследования в теории чисел. Он был целиком поглощён профессиональными и личными проблемами. В основном теорема Жермен оставалась неизвестной. В 1823 году Лежандр упоминает её в своей работе, где описывает своё доказательство последней теоремы Ферма для случая, когда В своих исследованиях по теории чисел Софи Жермен полагалась на направляющее влияние Гаусса. Когда их переписка прекратилась, она стала искать новые задачи и новых наставников. В 1809 году она заинтересовалась темой, которая впоследствии легла в основу её самых лучших работ. Она пыталась объяснить классические эксперименты Эрнста Ф. Хладни, немецкого физика, исследовавшего колебания упругих пластин. В своих экспериментах Хладни насыпал мелкий песок на стеклянную пластинку. Затем он проводил смычком по ребру пластинки, вызывая колебания. Песок отскакивал от вибрирующих областей и собирался в «узлах», точках, остававшихся неподвижными. Через несколько секунд пластинка покрывалась рядом песчаных кривых. Конфигурация рисунка была симметричной и весьма эффектной — она состояла из звёзд и других геометрических фигур (см. рисунок ниже). Общий рисунок зависел от формы пластины, положения опор и частоты вибрации.
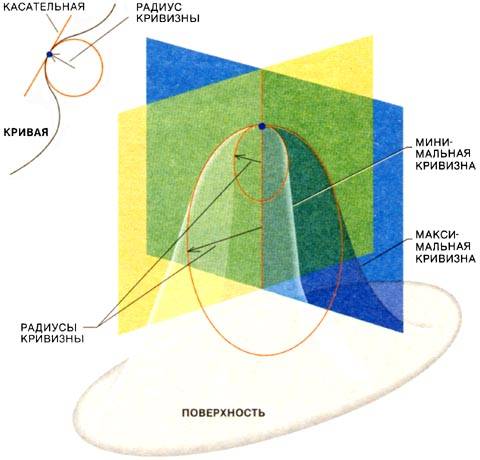
Во время своего визита в Париж в 1808 году Хладни продемонстрировал свои опыты перед аудиторией из 60 математиков и физиков Первого класса Французского института, отделения Французской академии наук. Опыты Хладни привели учёных в такое изумление, что они попросили его повторить свои опыты перед Наполеоном. Увиденное произвело на императора впечатление, и он согласился, что учёным Первого класса следует учредить специальную медаль весом в один килограмм золота и присудить её тому, кто сумеет дать теоретическое объяснение опытов Хладни. В 1809 году был объявлен конкурс и установлен срок его окончания для подведения итогов. Срок истекал через два года. Жермен ухватилась за эту возможность. На протяжении более десяти лет она будет пытаться построить теорию упругости, конкурируя или сотрудничая с самыми выдающимися математиками и физиками. Она будет испытывать гордость от сознания того, что внесла свой вклад в исследования, находившиеся на переднем крае науки XIX века. Тем не менее Жермен останется в стороне от научного сообщества. Этикет требовал, чтобы она получала письмо с официальным приглашением всякий раз, когда хотела посетить научное учреждение. Приглашавший должен был обеспечить ей транспорт и сопровождение. Эти формальности мешали ей свободно обсуждать с другими учёными интересовавшие её вопросы. Как следствие этих ограничений, ей пришлось преодолеть немало трудностей, чтобы переключиться с теории чисел на теорию упругости. Чтобы войти в курс теории вибраций, она обратилась к таким книгам, как «Аналитическая механика» Лагранжа и работам Эйлера о колебаниях упругих стержней. Жермен пыталась объяснить поведение упругих пластин, применяя методы, которыми пользовался Эйлер. Он предполагал, что прикладываемая к стержню сила вызывает внутреннее упругое противодействие, и утверждал, что сила упругости в любой точке стержня пропорциональна его кривизне. Под влиянием работ Эйлера Жермен стремилась к тому, чтобы построить аналогичную гипотезу. Она предположила, что в любой точке поверхности сила упругости пропорциональна сумме величин кривизны двух главных кривых в этой точке. Главные величины кривизны представляют собой максимальное и минимальное значение кривизны всех кривых при пересечении поверхности перпендикулярными к ней плоскостями.
В 1811 году Жермен оказалась единственным участником конкурса, но её работа не была удостоена премии. Она не сумела вывести свою гипотезу из физических принципов, да и не могла сделать этого в то время, поскольку ей не хватало знаний в математическом анализе и вариационном исчислении. Тем не менее её работа способствовала дальнейшему прогрессу в этой области. Лагранж, бывший одним из членов жюри конкурса, исправил некоторые ошибки в вычислениях Жермен и вывел уравнение, которое, как он полагал, могло описывать фигуры Хладни. Согласно рассуждениям Лагранжа, если где В 1811 году конкурс был продолжен ещё на два года, и снова Жермен была единственным его участником. Она продемонстрировала, как уравнение Лагранжа порождает фигуры Хладни в нескольких простых случаях. Однако она не смогла вывести уравнения Лагранжа из физических законов. За свою работу она была удостоена похвальной грамоты учёных Первого класса. Приблизительно в это же время на интеллектуальную территорию Жермен начал вторгаться Симеон Дени Пуассон. В дальнейшем ему было суждено стать её главным соперником. В отличие от Жермен Пуассон подошёл к теории упругости, располагая всеми средствами, доступными учёному XIX века. Пуассон поступил в Высшую политехническую школу в 1789 году в возрасте 17 лет. Лагранж и Лаплас заметили его способности в решении математических задач и хорошее абстрактное мышление. При поддержке Лапласа Пуассон быстро продвигался по академической лестнице. Он стал профессором в Политехнической школе и на факультете естественных наук в Париже. Он часто посещал заседания знаменитого научного общества Société d'Arcueil, куда приходили некоторые самые выдающиеся учёные, чтобы обсудить интересные работы или продемонстрировать новые эксперименты. Руководили деятельностью общества Лаплас и Клод Луи Бертолле, а Пуассон был консультантом в области математики. В 1812 году Пуассон, уже успевший проникнуть в самое сердце научного сообщества, был избран в Первый класс. Пуассон стремился объяснить колебания упругих пластин на основе физических законов Ньютона и его физической модели. Начав с предположения, что пластина состоит из молекул, которые взаимно притягивают и отталкивают друг друга, Пуассон затем сделал ряд других, казалось, вполне разумных предположений. Рассуждая таким образом, он вывел чрезвычайно сложную формулу и, упростив её, пришел к уравнению Лагранжа. По современным представлениям допущения Пуассона кажутся абсурдными, и его попытка вывести уравнение Лагранжа была успешной лишь потому, что он знал о работе Жермен и Лагранжа. В 1814 году Пуассон опубликовал статью об упругих пластинах. Как член Первого класса, он не участвовал в конкурсе. Но его коллеги считали, что Пуассон нашёл физическое объяснение для фигур Хладни. Приз же остался никому не присвоенным. «Я очень сожалела о том, что не знала содержания работы Пуассона, — писала Жермен в 1815 году в своем эссе, посвящённом теории упругости. — Я тратила драгоценное время, ожидая публикации». В этом эссе она подвергла критике подход Пуассона, пытаясь предложить своё собственное объяснение. Жермен постулировала, что упругая сила пропорциональна приложенной извне силе и пропорциональна деформации поверхности. Сила в каждой заданной точке пропорциональна сумме всех значений кривизны для кривых, проходящих через эту точку. Затем она показала, что сумма всех изгибов сводится к сумме максимальной и минимальной кривизны. И наконец, она вывела уравнение Лагранжа из последней суммы. Это эссе стало третьей попыткой Жермен выиграть конкурс, членами жюри которого на этот раз были Лежандр, Лаплас и Пуассон. Они не могли принять её постулата о том, что результат воздействия — деформация — обязательно пропорционален самому воздействию, т.е. приложенной силе. На самом деле пройдут десятилетия, прежде чем этому будет найдено объяснение. При этой оговорке, жюри присудило Жермен премию Первого класса. Жермен не явилась на церемонию вручения награды. Может быть она считала, что судьи не оценили по достоинству её работу, или же она просто не хотела появляться на публике. Для Жермен присуждение премии явилось формальным признанием её научной компетентности. Это придало ей уверенности и повысило авторитет. Однако учёные не выразили ей должного уважения. Пуассон послал ей немногословное формальное поздравление. Он избегал серьёзных дискуссий с ней и игнорировал её при встречах в обществе. Несколько лет назад она рассматривала себя как слабенького новичка в компании гигантов. Теперь она уже не испытывала восторга от своих коллег. Вскоре она воспряла духом, подружившись с Жаном Батистом Жозефом Фурье. Жермен и Фурье, оба пострадали из-за соперничества с Пуассоном, и оба одинаково не любили его. Благодаря Фурье, Жермен начала принимать участие в деятельности парижского научного сообщества. Она посещала заседания Академии наук и была первой женщиной, которая приходила на эти заседания в личном качестве, а не как супруга кого-либо из её членов. В 20-х годах XIX века у неё возникли честолюбивые планы в области теории чисел, где она надеялась усовершенствовать свои доказательства и продолжить ранее начатые работы. Жермен и Лежандр работали в этой области как равноправные партнёры. Она также опубликовала обзор своих работ по теории упругости. В это время Жермен интересовалась различными областями научного знания и общалась с интеллектуальной элитой. Всем импонировали её неуёмное любопытство и присущее ей обаяние. Хотя Жермен определённо заслужила своими работами учёной степени, она так никогда её и не получила. В 1830 году Гаусс не сумел убедить профессуру Гёттингенского университета присвоить ей звание почётного доктора наук. Заболев раком груди, Софи Жермен после двухлетней борьбы с болезнью умерла 27 июня 1831 года в возрасте 55 лет. В свидетельстве о смерти против её фамилии значилось rentere: «персона, располагавшая частными средствами», что на практике означало «независимая женщина». Перед смертью она набросала вчерне философское эссе, которое не успела закончить. Оно было опубликовано посмертно под заголовком «Общие рассуждения о науках и литературе». В своём эссе она пыталась выделить интеллектуальный процесс во всех видах человеческой деятельности и полагала, что интеллектуальная вселенная наполнена аналогиями. Человеческий дух, согласно её представлению, распознает эти аналогии, что приводит в конечном итоге к открытию природных явлений и законов мироздания. Нам же в свою очередь следовало бы распознавать аналогии между жизнью Софи Жермен и нашей собственной, с тем чтобы эти аналогии помогли нам стремиться к совершенству перед лицом предрассудков общества. Литература 1. S. Germain. Examen des Principles Qui Peuvent Conduire à la Connaissance des Loisde l'Équilibre et du Mouvement des Solides Élastiques. In: Annales de Chimie et de Physique, 1828, Series 2, v. 38, pp. 123–131. 2. L. L. Bucciarelli and N. Dworsky. Sophie Germain: An Essay in the History of the Theory of Elasticity. D. Reidel Publishing Company, 1980. 3. A. Dahan-Dalmédico. Mécanique et Théorie des Surfaces: Les Travaux de Sophie Germain. In: Historia Mathematica, 1987, v. 14, No. 4, pp. 347–365. 4. A. Dahan-Dalmédico. Étude des Méthodes et des "Styles" de Mathématisation: La Science et l'Élasticité. In: Sciences à l'Époque de la Révolution. Paris, Librairie Blanchard, 1988. Amy Dahan-Dalmédico "Sophie Germain"
Scientific American. Издание на русском языке № 2. Февраль 1992. С. 60–66
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Софи Жермен // Эми Дайан-Дальмедико |
|
[time: 20 ms; queries: 7]
11 Мар 2026 02:21:31 GMT+3 |


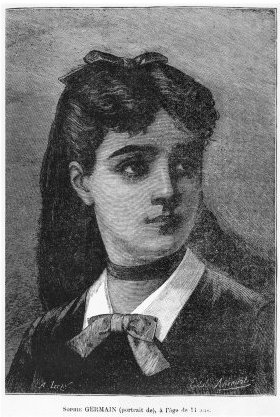


 Интервью о пути в науку, научной среде и популяризации науки с кандидатом физико-математических наук, заведующим Лабораторией нейроинтеллекта и нейроморфных систем НБИКС «Курчатовский Институт» Михаилом Бурцевым.
Интервью о пути в науку, научной среде и популяризации науки с кандидатом физико-математических наук, заведующим Лабораторией нейроинтеллекта и нейроморфных систем НБИКС «Курчатовский Институт» Михаилом Бурцевым. О продуктивности Коши-математика свидетельствует целый ряд терминов, определений и понятий, вошедших в науку, таких, как признак Коши, критерий Коши, задачи Коши, интеграл Коши, уравнения Коши–Римана и Коши–Ковалевской, относящиеся к разным разделам математического анализа, математической физики, теории чисел, и других дисциплин. Всего же он написал 700 работ (по другим источникам 800), с неимоверной легкостью переходя от одной области научного знания к другой.
О продуктивности Коши-математика свидетельствует целый ряд терминов, определений и понятий, вошедших в науку, таких, как признак Коши, критерий Коши, задачи Коши, интеграл Коши, уравнения Коши–Римана и Коши–Ковалевской, относящиеся к разным разделам математического анализа, математической физики, теории чисел, и других дисциплин. Всего же он написал 700 работ (по другим источникам 800), с неимоверной легкостью переходя от одной области научного знания к другой. Это фильм в режиме включенного наблюдения, история о реальном исследовании, которое проводится в научно-исследовательском центре «Дискретизация в геометрии и динамике» Технического университета в Берлине. В центр постоянно приезжают математики русского происхождения, работающие по всему миру. Процесс ведения научных дискуссий, запечатленный на камеру, является уникальным по силе воздействия материалом: зритель становится свидетелем размышлений ученых, возникновения гениальных идей, погружается в работу команды и разделяет весь спектр эмоций участников.
Это фильм в режиме включенного наблюдения, история о реальном исследовании, которое проводится в научно-исследовательском центре «Дискретизация в геометрии и динамике» Технического университета в Берлине. В центр постоянно приезжают математики русского происхождения, работающие по всему миру. Процесс ведения научных дискуссий, запечатленный на камеру, является уникальным по силе воздействия материалом: зритель становится свидетелем размышлений ученых, возникновения гениальных идей, погружается в работу команды и разделяет весь спектр эмоций участников. Математика — это не только замечательная точная наука, но еще и удивительные человеческие судьбы. Девушка из Ирана по имени Мариам Мирзахани стала первой в мире женщиной, получившей Филдсовскую медаль — пожалуй, самую престижную награду в математике. Мариам показала как иранским ученым, так и простым людям, в частности женщинам, — чего может добиться человек собственным умом и собственной настойчивостью.
Математика — это не только замечательная точная наука, но еще и удивительные человеческие судьбы. Девушка из Ирана по имени Мариам Мирзахани стала первой в мире женщиной, получившей Филдсовскую медаль — пожалуй, самую престижную награду в математике. Мариам показала как иранским ученым, так и простым людям, в частности женщинам, — чего может добиться человек собственным умом и собственной настойчивостью. Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами…
Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами… Лекция прочитана 4 июля 2006 года в поселке Московский в рамках II конференции лауреатов Всероссийского конкурса учителей математики и физики фонда «Династия».
Лекция прочитана 4 июля 2006 года в поселке Московский в рамках II конференции лауреатов Всероссийского конкурса учителей математики и физики фонда «Династия». Назвать гениев математики очень просто. Для этого достаточно открыть любой список под названием «100 великих ученых», где из раза в раз перечисляются все те же имена: Евклид, Ньютон, Декарт, Гаусс, Риман, Архимед, Лейбниц и т.д. Но история науки немыслима и без ученых, чья известность пусть не столь широка, но чьи открытия лежат в основе сегодняшнего научного знания. Представляем перевод статьи, в которой представлена альтернативная десятка гениев математики.
Назвать гениев математики очень просто. Для этого достаточно открыть любой список под названием «100 великих ученых», где из раза в раз перечисляются все те же имена: Евклид, Ньютон, Декарт, Гаусс, Риман, Архимед, Лейбниц и т.д. Но история науки немыслима и без ученых, чья известность пусть не столь широка, но чьи открытия лежат в основе сегодняшнего научного знания. Представляем перевод статьи, в которой представлена альтернативная десятка гениев математики. Теплым весенним утром Джун Ху шел в зал Макдоннелла Пристонского университета, где его ждали студенты. Однако он не был уверен, что идет в нужном направлении. Ху работает в элитарном Институте перспективных исследований, который располагается неподалеку от студгородка Принстона. Будучи сотрудником института, Ху не обязан преподавать. Тем не менее, он вызвался прочитать студентам продвинутый курс по коммутативной алгебре.
Теплым весенним утром Джун Ху шел в зал Макдоннелла Пристонского университета, где его ждали студенты. Однако он не был уверен, что идет в нужном направлении. Ху работает в элитарном Институте перспективных исследований, который располагается неподалеку от студгородка Принстона. Будучи сотрудником института, Ху не обязан преподавать. Тем не менее, он вызвался прочитать студентам продвинутый курс по коммутативной алгебре. Математика — универсальный язык Вселенной, фундамент, на котором основаны все другие науки. Как человечество смогло открыть тайны этого универсального языка? Начиная с древнейших времен, прослеживается история математики до наших дней и завершается рассказом о наиболее важных проблемах современности. Их решение позволит лучше понять устройство нашего мира.
Математика — универсальный язык Вселенной, фундамент, на котором основаны все другие науки. Как человечество смогло открыть тайны этого универсального языка? Начиная с древнейших времен, прослеживается история математики до наших дней и завершается рассказом о наиболее важных проблемах современности. Их решение позволит лучше понять устройство нашего мира. О Москве, математике и музыке мы поговорили с Александром Буфетовым, ведущим научным сотрудником Математического института имени В.А. Стеклова, ведущим научным сотрудником ИППИ имени А.А. Харкевича, профессором факультета математики Высшей школы экономики, директором исследований Национального центра научных исследований во Франции (CNRS).
О Москве, математике и музыке мы поговорили с Александром Буфетовым, ведущим научным сотрудником Математического института имени В.А. Стеклова, ведущим научным сотрудником ИППИ имени А.А. Харкевича, профессором факультета математики Высшей школы экономики, директором исследований Национального центра научных исследований во Франции (CNRS).