Лекция академика РАН, доктора физико-математических наук, председателя научного совета РАН по нелинейной динамике, зав. Сектором математической физики в Физическом институте РАН им. Лебедева, профессора Университета Аризоны (США), дважды лауреата Государственной премии, лауреата медали Дирака Владимира Евгеньевича Захарова, прочитанной 27 мая 2010 года в Политехническом музее в рамках проекта “Публичные лекции Полит.ру”.

Текст лекции

Владимир Захаров (фото Наташи Четвериковой)

Спасибо. Мне очень приятно, что я выступаю здесь. Это честь — быть приглашенным прочесть лекцию в Политехническом музее.

Я расскажу о довольно обширной области знания, которая является предметом моего интереса с юных лет. Моя докторская диссертация, защищенная в 1971 году, была в значительной степени посвящена тем вопросам, о которых я буду говорить сегодня. Эта область, с одной стороны, является частью физики, в том числе экспериментальной. С другой стороны, она имеет отношение к океанологии — к тому, что называют “физической океанографией”. Кроме того, эта область затрагивает математические аспекты. Возможно, аудитория будет очень удивлена, узнав, что знаменитая работа Перельмана родственна тем задачам, которые ставит перед собой эта наука.

С чего же мы начнем? С чего-то очень простого. Прошу прощения: я так и не научился набирать на компьютере научные тексты. Обычно это делает жена, но сейчас она забастовала и сказала, что занята. Помогали мне мои ученики. В общем, большая часть текста просто написана от руки и отсканирована. Я надеюсь, вы этот факт мне простите.

Вот план моего доклада. Прежде всего, экстремальные волны возникают в природе в результате фокусировки. Фокусировка — дело вполне обычное и знакомое всем с детства, когда бралась лупа и с ее помощью что-нибудь выжигалось. Но дело в том, что в природе лупу устраивает сама природа, сами экстремальные волны устраивают себе подобные лупы. Отсюда и их происхождение.

Самым простым и наиболее классическим примером экстремальных волн, самопроизвольно возникающих в природе, является самофокусировка света. Ее суть состоит в следующем: если вы возьмете очень мощный лазерный пучок и попытаетесь его пропустить через стекло, то ничего хорошего из этого не выйдет — стекло разлетится. Этот самый пучок света из равномерного, однородного превратится в весьма хаотический. Он породит много различных фокусов, где будет сконцентрирована большая энергия и произойдет выжигание материала. Можно было бы даже, наверное, попросить экспериментаторов, чтобы они дали такой кусочек кварца, внутри которого будет видно множество пузырьков. Это результат процесса самопроизвольной фокусировки света, или самофокусировки.

Самофокусировка имеет свою математическую модель. Эта модель обладает свойством математических моделей, применяемых в физике: она универсальна и применима к очень обширному классу задач. Так, например, одно и то же уравнение описывает распространение нелинейных волн в кристалле и в диэлектрике. Похожее уравнение описывает распространение волн на воде. Поведение волн в плазме описывает немного более сложное уравнение: в нем есть другие, родственные, но достаточно своеобразные эффекты.

Далее, я перейду к следующему пункту. Прошу прощения за мою несколько неуклюжую графику. Здесь я изобразил линзу.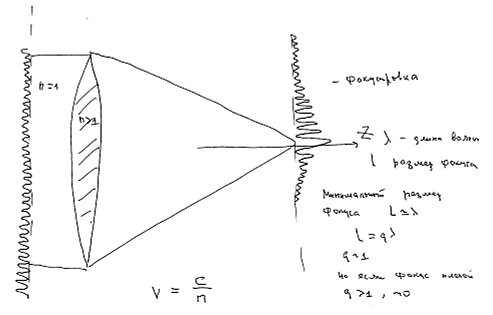

Это обычная фокусировка, всем знакомая с детства. Если бы фронт волны был плоским, то в районе фокусов он имел бы максимум. Все изобретатели, конструкторы объективов и телескопов, разумеется, стараются сделать этот максимум как можно более узким и острым (на это есть свои дифракционные пределы). Максимум можно несколько уменьшить искусным конструированием объектива, в лучших приборах он достигает приблизительно 0,7 длины волны, но никогда не бывает меньше 0,5.

Если фокусное расстояние объектива велико, то есть если максимум достаточно размыт, тогда волновое поле в фокальной плоскости описывается очень простым уравнением: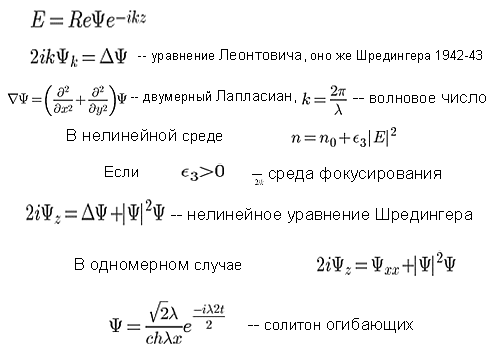

Люди, знакомые с квантовой механикой, скажут: “Бог мой, это же уравнение Шредингера для свободной частицы”. Так и есть. Эта аналогия была найдена достаточно поздно, во время войны, нашим замечательным физиком и не менее замечательным, благородным и достойным человеком Михаилом Александровичем Леонтовичем, создавшим школу по макроскопической физике в Институте атомной энергии. Это был человек необыкновенного благородства и высочайших моральных достоинств. Во время войны радиотехника была чрезвычайно важна, изучали распространение радиоволн вокруг земной поверхности, и он нашел такое упрощающее обстоятельство. Это называется “приближение Леонтовича”.

Фокусировка происходит за счет того, что внутри линзы коэффициент — показатель преломления n — больше единицы и, соответственно, скорость распространения световых волн немножко меньше, чем в вакууме. Это свойство стекла: чем больше n, тем лучше стекло преломляет.

В природе все среды в той или иной степени нелинейны, то есть у них показатель преломления зависит от амплитуды распространяющейся волны. Если волна имеет малую амплитуду, то это несущественный эффект. Если же, скажем, лазерный луч, очень мощный, то эффект уже весьма заметный. Коэффициент преломления, конечно, усреднено реагирует на эту волну, то есть входит в квадрат модуля этой амплитуды. Если коэффициент положительный, то среда называется фокусирующей. В таком случае к уравнению Леонтовича нужно добавить один нелинейный член — и получится нелинейное уравнение Шредингера. Это и есть чрезвычайно общая модель, описывающая множество явлений и применимая к очень многим задачам.

Здесь у меня взята продольная координата вдоль направления луча. Получается уравнение, которое можно рассматривать как нестационарное уравнение, если заменить производную по z на производную по времени. Пусть пучок в поперечном направлении зависит от одной только координаты. Тогда линза цилиндрическая, а фокус есть линия. Теперь у уравнения есть замечательное решение, которое называется “солитон огибающих”. Данная модель — нелинейное одномерное уравнение Шредингера — обладает совершенно удивительным свойством: это вполне интегрируемая гамильтонова система, то есть у него имеется бесконечное количество интегралов движения, и в каком-то смысле можно построить его аналитически точное решение для достаточно широкого класса начальных условий.

Дальше выясняется, что когда мы будем строить эти решения для периодических граничных условий, окажется, что мы немедленно попадем в такую математику, которая в начале ХХ века безусловно считалась вершиной всей математической мысли. Это так называемая “теория абелевых функций”. И нам придется искать решение в виде θ-функций, над алгебраическими кривыми. Это весьма сложная наука, в которой до сих пор есть важные нерешенные вопросы.

Я просто хочу показать, как короток шаг от простой физической до крайне утонченной математической задачи. Для физики нелинейных волн это — типичное явление.

Если взять 2 солитона и пустить их друг на друга, они будут упруго взаимодействовать, упруго рассеются и разойдутся, при этом приобретя некоторые сдвиги.

Самое поразительное, что весь этот сложный процесс можно описать в элементарных функциях, просто линейной комбинацией экспонент, рациональными функциями от всего двух экспонент. Вот такой замечательный факт. А если бы было две периодические цепочки солитонов, тогда нам пришлось бы работать с θ-функциями Якоби на определенных гиперэллиптических кривых.

Здесь я должен с гордостью сказать, что факт интегрируемости этой системы был открыт в моей работе с Алексеем Борисовичем Шабатом в 1971 году и представлял собой существенную часть моей докторской диссертации (и эта работа является четвертой по индексу цитируемости среди всех работ российских авторов: всего на нее зарегистрировано 2713 ссылок на май прошлого года, и с тех пор, наверное, еще больше добавилось).

Теперь рассмотрим двумерное уравнение, то есть более близкое к реальности, когда фокус — настоящий точечный, а не линейный. Тогда уравнение совсем немного изменится, станет аксиально-симметричным, но разница здесь колоссальная. Уравнение перестает быть интегрируемым, не удастся даже построить точного солитонного решения (оно существует, но его можно сосчитать только на компьютере — так называемая “мода Таунса”). Но тут есть такой удивительный момент: у этого уравнения интегралов движения, грубо говоря, столько же, сколько у всех остальных систем, то есть у него дополнительно есть энергия, импульс, число квазичастиц и гамильтониан. Но если этот гамильтониан отрицателен (а он может быть и положительным, и отрицательным, в зависимости от начальных условий), тогда любое начальное условие закончится коллапсом, решение превратится в бесконечность за конечное время и на конечном расстоянии (время у нас играет роль расстояния).

Этот результат тоже был получен в России, но не мной, увы, а в Нижнем Новгороде, тогдашнем Горьком, академиком Владимиром Ильичом Талановым (тогда он еще не был академиком) и двумя его учениками. Когда Владимира Ильича выбирали в академики, я вышел и сказал, что за один этот результат — а у него есть много других работ — его, безусловно, нужно выбрать академиком, потому что это результат редкий по красоте и по значительности. Слава Богу, его действительно выбрали.

Потом возник вопрос, как устроено поведение вблизи особенности.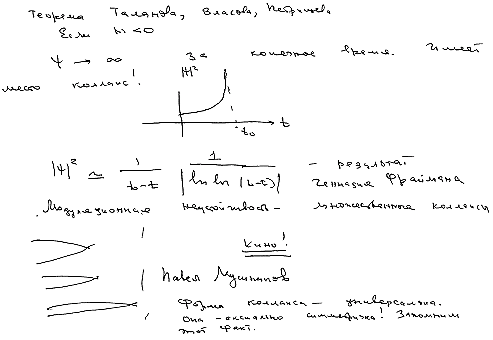

Особенность уходит в бесконечность каким-то образом, но каким? Оказалось, труднейшая задача. Очень долго с ней возились. У меня был единственный в жизни случай, когда я написал и послал в журнал неправильную статью, где была модель этого поведения. К счастью, я сам обнаружил, что она неправильная и забрал статью. Она уже была набрана, у меня потом были неприятности с редакцией журнала: они требовали с меня штраф, но обошлось частичной потерей репутации.

Правильный ответ был найден замечательным физиком Геннадием Фрайманом. Это очень скромный человек, который тоже живет в Нижнем Новгороде. Оказалось, что в асимптотике присутствует двойной логарифм, что бывает чрезвычайно редко. Эта теория странным образом оказалась похожей на теорию гамма-альфа-распада ядер. Прошло примерно лет 5 — и этот результат стали со страшной силой воспроизводить на Западе. Нам пришлось доказывать, что приоритет принадлежит здесь Гене Фрайману. Теперь это уже признанный факт.

Таким образом, здесь мы видим явление самофокусировки, то есть возникает особенность за конечное время. Сама среда начинает вести себя как линза (она сама фокусирует свет). Вы скажете: “Но почему она ведет себя как линза? Представим, что мы пустим совершенно плоскую идеальную волну, так, что все будет однородно, и показатель преломления изменится немного, но будет все равно постоянным — откуда же линза возьмется?” Оказывается, что такое распространение неустойчиво, и если его чуть-чуть возмутить (а всегда есть какие-то возмущения), они начинают нарастать и создают тогда не одну, а множество линз. Пучок разбивается на множество пучков, которые ведут себя случайным образом. Если это одномерная задача, можно все так или иначе сосчитать, хотя это очень трудно, несмотря на полную интегрируемость. В двумерной — только численно.

Я сейчас примерно покажу, что получается. Здесь рассматривается решение нелинейного уравнения Шредингера. Отложены линии уровня квадрата модуля. Видно, что время от времени возникают случайные точки — это фокусы. Конечно, это не совсем то уравнение: к нему добавлено еще затухание, которое сжигает энергию, попадающую в фокус, и расходится, в результате чего возникают бегущие в сторону волны. (videoclip: psilin)

В следующем фильме представлено то же самое явление в аксонометрической проекции. Видите, как возникают экстремальные фокусы. Это, конечно, чудо вычислительной техники. Численный эксперимент был сделан в городе Альбукерке в университете Нью-Мексико, где ученик моего ученика (члена-корреспондента РАН Е.А. Кузнецова) Паша Лушников сейчас профессор. Ему помогает одна русская девушка. Вот мы видим экстремальные волны.

Явление самофокусировки нежелательно. Статистическую теорию этого явления сейчас пытаются строить. Задача состоит в том, чтобы вычислить функцию распределения вероятности для появления таких редких событий. В общем, это более или менее делается, возникают такие “жирные хвосты” на функции распределения вероятностей.

Вопрос из зала: Мы сейчас рассматриваем случай, когда есть среда и на нее падает плоская волна?

Владимир Захаров: Ну, если хотите, это среда. Время — это длина, вдоль которой все происходит. Падает очень интенсивная волна; граничные условия — периодические. Она создает фокусы. Вблизи фокуса уравнение ренормализуется, то есть там добавляется затухание, которое поглощает часть энергии, попадающей в фокус, так что фокус исчезает.

Вопрос из зала: А фокус — это разрыв?

Владимир Захаров: Нет, в фокусе возникает концентрация конечного числа квазичастиц в очень малой области. Как видно, это происходит очень быстро и взрывным образом.

Явление самофокусировки изучают, потому что оно весьма вредное. Кроме того, что оно ломает стекла, еще (и это, по-видимому, главное) это явление ограничивает возможность создания очень мощных лазеров на твердых диэлектриках. Оно, кстати говоря, и в воздухе тоже есть. Если пропустить очень мощный лазер через атмосферу, то всё пройдет по той же модели. Это явление называется филаментизацией. Только в данном случае вместо точек будут возникать жгуты. Есть определенная инерционность волн: вдоль них будут возникать такие жгуты, в которых содержится энергия.

Это весьма сложное явление, которое сейчас подробно изучают в связи с тем, что оно имеет прикладное значение. У нас сейчас очень остро стоит вопрос об энергетике (нефть-то скоро кончится), и одно из решений проблемы — использовать солнечную энергию. Предлагается, например, вывести на орбиту большой алюминиевый лист размером 100 на 100 метров, и чтобы это слегка изогнутое зеркало ловило солнечный свет и направляло его на Землю. На таком спутнике будет фокус, где солнечный свет будет использоваться как оптическая накачка для мощного лазера. Его направят на Землю, на приемную станцию. Такой проект существует. Между прочим, мой ученик Саша Рубенчик занимается как раз этим делом в Ливерморской лаборатории, США. Беда, однако же, состоит в том, что когда этот лазерный пучок будет проходить через атмосферу, у него будут неприятности: с ним начнутся случайные фокусировки, поэтому надо делать его не слишком интенсивным, а для этого придется создавать большую приемную станцию.

Я вам говорил с самого начала, что в оптике никак нельзя сделать фокус меньше длины волны. Уравнение Леонтовича (оно же нелинейное уравнение Шредингера) работает только тогда, когда у нас имеется огибающая, то есть когда фокус достаточно размазанный.

В плазме, оказывается, можно сделать фокусировку значительно меньших размеров, чем длина волны. В плазме есть такие волны — они называются ленгмюровские — волны разделения заряда. Когда в плазме есть положительный и отрицательный заряды, электроны и ионы разделяются и возникают колебания. У них тоже есть самофокусировка, как и у большинства остальных волн. Но вот что интересно: в результате самофокусировки (если мы подойдем к размеру порядка длины волны) у них в плазме может образоваться зона пониженной плотности, которая называется “каверна”. Она будет сжиматься до размера уже в десятки раз меньшего, чем длина волны. Она будет сжиматься, сохраняя имеющуюся там энергию. Конечно, плотность энергии будет возрастать, и в конце концов эта энергия излучится в виде быстрых электронов.

Это явление называется коллапсом ленгмюровских волн. Теоретически оно было предсказано в 1971 году. Эта моя работа также включена в число наиболее цитируемых российских авторов, но уже находится в конце списка — там примерно 1500 ссылок (меньше людей занимается плазмой, чем нелинейной оптикой, и математически имеющиеся там уравнения не столь замечательны). Экспериментально это явление обнаружено сравнительно недавно. Это очень трудный эксперимент.

Я думаю, сейчас в связи с делом Петрика всем известно имя академика Эдуарда Павловича Круглякова, председателя комиссии по борьбе с лженаукой. Как раз он со своими сотрудниками это явление экспериментально обнаружил в 2002 году в Институте ядерной физики в Новосибирске. Я рад подчеркнуть тот факт, что он не только борец за чистоту науки, но и реально действующий ученый очень высокого уровня. Вот его экспериментальная установка.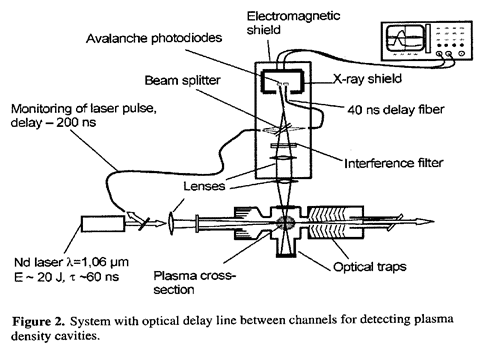

Здесь пучком возбуждается плазма, сверху она просвечивается лазером, и вот — ученые видят образования каверн, в которых как раз и заперто излучение. Эта работа достаточно широко известна в мире.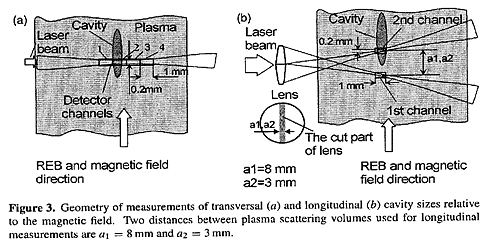

Другое экспериментальное подтверждение коллапса было получено со спутников, потому что это явление типично для солнечного ветра и для междупланетной плазмы. Например, в 1997 году спутник Улисс летал на довольно большом расстоянии от Земли и измерял электрическое поле, идущее от солнца. Продольного поля в направлении света вообще не должно быть: волны, как известно, поперечны. В плазме, однако же, бывают продольные волны. Они сконцентрированы в виде отдельных выбросов. Размер большой штуки около 100 метров. Размер каверны у Круглякова равен 2 миллиметрам, а здесь 100 метров — это, конечно, космические масштабы. Удивляться такому не приходится. Коллапс ленгмюровских волн, такая самопроизвольная концентрация волновой энергии в очень малых объемах (как мы видим, здесь логарифмический масштаб, и я обращаю на это внимание) означает, что поле приблизительно в 100 раз больше, а энергия — квадрат поля — в 10000 раз больше, чем в окружающей среде. Это, конечно, экстремальная волна, что показывает, что явление экстремальных волн достаточно универсально и многообразно.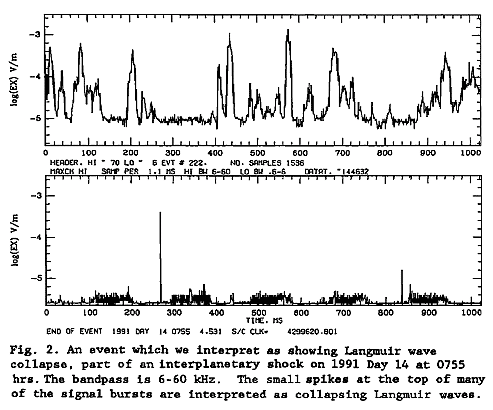

Дальше я немного скажу о том, что странным образом имеет отношение к работе Перельмана. Если мы рассмотрим риманово пространство — многообразие, снабженное метрикой, — по метрическому тензору можно построить тензор Риччи. Это очень сложное выражение (оно заняло бы полстраницы) можно найти, скажем, в учебниках теории поля Ландау и Лифшица. Но это дифференциальный оператор второго порядка, очень сильно нелинейный. Если метрический тензор почти близок тривиальному, у него всего одна компонента g_oo, то тензор Риччи — это, грубо говоря, оператор Лапласа от этой самой g_oo. Тогда g_oo есть не что иное, как гравитационный потенциал.

Уравнение Эйнштейна в пустоте представляет собой требование, чтобы тензор Риччи был равен нулю. Это уравнение, вообще говоря, в четырехмерном пространстве, значит, что метрический тензор g(ik) содержит 10 функций от четырех переменных. Если мы найдем частное решение, вместо 10 функций возникнет у нас всего 3 независимых функции, будет симметричная матрица 2x2, зависящая от двух переменных. Если она зависит от двух переменных, будут некоторые уравнения (я их не пишу, чтобы не перегружать), но они окажутся тоже интегрируемыми, как нелинейное уравнение Шредингера. У этих уравнений тоже есть солитонные решения.

А вот теперь догадайтесь с первого раза, что есть солитонное решение этих уравнений.

Голос из зала: Черная дыра.

Владимир Захаров: Правильно. Совершенно точно, черная дыра. Причем именно простейшее решение со всеми параметрами есть наиболее сложный вид черной дыры, то есть вращающаяся заряженная черная дыра, так называемая “метрика Керра”.

А теперь о том, какое это имеет отношение к Перельману. Вот какое. Значит, у нас есть 2 тензора — метрический и тензор Риччи. Тензор Риччи выражается через метрический при помощи вторых производных.

Давайте напишем вот такое уравнение: производная от метрического тензора по времени равна тензору Риччи. Это уравнение напрашивается, хотя время — не настоящее, конечно, а “искусственное”. Это естественное уравнение, потому что только 2 тензора можно построить второго ранга, а остальные — уже более высокого (из тензора кривизны четвертого ранга тензор Риччи получается сверткой с метрическим тензором). Данное уравнение описывает так называемый “поток Риччи”. Впервые его придумал профессор Ричард Гамильтон примерно в 1995 году.

Ясно, что эволюция метрического тензора под действием тензора Риччи проходит без изменений топологических свойств этого многообразия. Скажем, если у него внутри есть какие-то дыры, то оно так и должно сохраняться. Это, однако, не совсем верно, потому что возникают своеобразные перетяжки. Представьте себе поведение бублика, у которого происходит склеивание по одному направлению: радиус стремится к нулю. Нужно вот здесь разрезать этот бублик, произойдет акт хирургии.

Это уравнение, оказывается, тоже имеет решение, взрывающееся за конечное время, подобно нелинейному уравнению Шредингера. Если вы видели в том фильме, где решалось полное двумерное уравнение Шредингера, эти дырочки-особенности совершенно симметричны. Есть гипотеза, что и здесь тоже будет максимально симметричное поведение вблизи особенности, а максимально симметричное поведение — это метрика сферы. Перельман доказал тот факт, что особенность в этом уравнении, в потоке Риччи, ведет себя таким образом: она взрывается. Поведение по времени легко восстанавливается (это t⁰-t²), а то, что вот здесь стоит, есть метрика трехмерной сферы. Этот абсолютно универсальный факт оказалось необычайно трудно доказать. Сам по себе, он и есть гипотеза Пуанкаре. В нее все верили, но доказать ее было технически необыкновенно сложно. А вот он сделал это. Замечательный, конечно, результат. Эта работа — одна из проблем, включенных в список Математического института Клея, за решение которой дают миллион долларов. Перельман эту проблему решил, от миллиона долларов он отказался, и все это знают.

Владимир Захаров (фото Наташи Четвериковой)

Но вот есть другая проблема, за которую миллион долларов пока не присудили, но тоже присудят, если она будет решена. Как мы говорим, экстремальные волны связаны с образованием особенностей. Математический аспект экстремальных волн — это образование особенностей в определенных классах уравнений, описывающих природные явления. Уравнения Эйнштейна, конечно, имеют особенности — гравитационный коллапс. Формирование черных дыр — хорошо изученная наука: решения строили еще в 30-е годы прошлого века; в искусственном, но чрезвычайно изящном уравнении Риччи решение найдено сейчас.

Что касается обычного уравнения гидродинамики (мы сейчас говорим об уравнении Навье-Стокса, которое описывает дозвуковое течение), то еще не решена проблема, может ли там быть особенность за конечное время. За решение этой проблемы тоже присуждают миллион долларов. Есть гипотеза, что если сделать 2 противоположно направленных вихря (а это будет неустойчивая конфигурация), то они должны склеиться, и в момент образования склеивания должна возникнуть особенность. Я потратил на эту задачу, наверное, лет 5 своей жизни, но успеха не добился. Я построил некоторые модели, но, к сожалению, только для бесконечно тонких вихрей: бесконечно тонкие вихри действительно склеиваются за конечное время, но у конечного размера вихрей там ничего не получается, и численный эксперимент тоже ничего не дает, так что этот вопрос остается открытым.

У меня остается еще немного времени. Давайте перейдем к другому файлу. Я хочу рассказать вам о еще одном типе экстремальных волн, а именно о волнах-убийцах в океане. Сейчас волны-убийцы — чрезвычайно модная тема, они у всех на слуху. Не далее как пару месяцев назад (март 2010 г.) такая волна очень сильно повредила лайнер около Марселя ("Полит.ру" - 2 пассажира погибли).

В течение многих лет ученые не верили морякам, которые говорили, что иногда бывает так, что в море возникает совершенно ниоткуда огромная волна, она ударяет по судну, и непонятно, что с ней делать, потому что время ее развития составляет несколько минут, десяток периодов волны. Морякам не особенно верили. Но со временем начали строить нефтяные платформы для того, чтобы бурить морское дно и добывать оттуда нефть, и, естественно, океанологи попросили строителей на каждую платформу поставить прибор для измерения уровня поверхности моря.

Собственно, это очень просто: сегодня обычный лазер ловит отраженный сигнал — и ничего более; в старые времена просто спускали проволочку, и по изменению сопротивления проволоки мерили высоту. Одна такая платформа стоит в северном море южнее побережья Швеции и называется Драупнир (“кольцо” Одина, верховного бога германо-скандинавской мифологии). Там стоит такой волномер. 1 января 1995 года на кривой записи формы поверхности была обнаружена одиночная волна, разница между нижней и верхней точкой которой составляла 26 метров.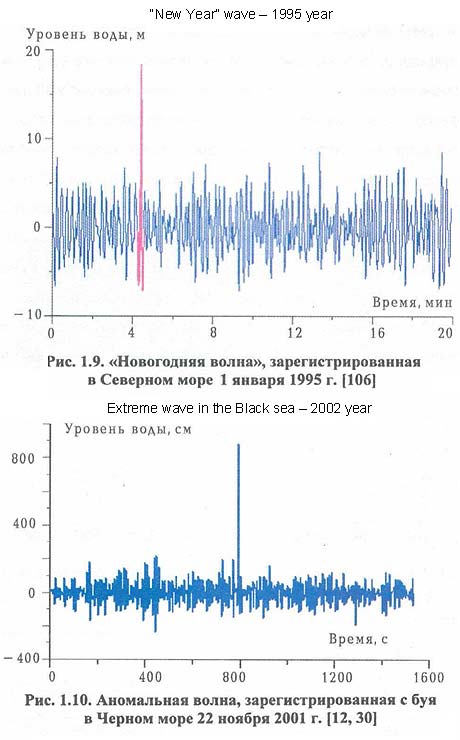

Платформу она не разломала, но дело было близко к этому. Заметим, что эта волна одиночная, и потому нелинейное уравнение Шредингера к ней применять нельзя, потому что она предполагает очень точный фокус, но работает оно, только когда фокус очень размыт.

Спустя семь лет аналогичная волна была измерена на Черном море в Геленджике, где есть станция Института океанологии. Это произошло 22 октября 2002 года. Волна, конечно, меньше — всего 8 метров, но если сравнивать с фоном, то получаем примерно то же самое.

Сейчас, по мере того, как стали запускать спутники и осуществлять мониторинг океана, эти волны наблюдаются систематически.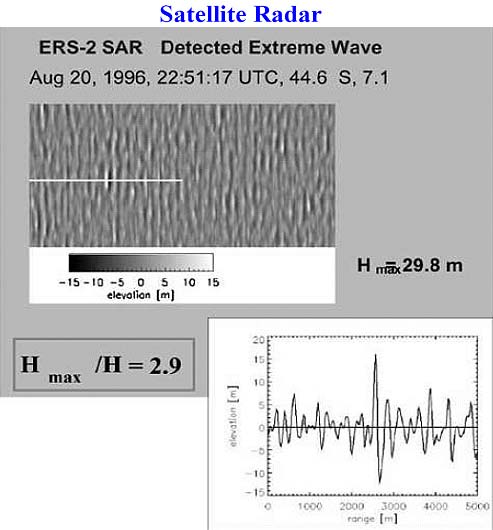

Заметим, что со спутника ее можно сфотографировать, но изучать очень трудно, потому что спутник быстро движется и скоро теряет ее из виду. Сейчас изобретают очень хитрые способы и подсвечивают океан двумя спутниками.

Вот волна высотой 29, почти 30 метров. Вот что происходит, когда такая волна ударяет по кораблю.

А вот результат встречи с волной-убийцей. Их называют “killer wave”, или “freak-wave” (грубо говоря, “чокнутая волна”), “rogue wave” (“волна-бандит”), “extreme wave” (“экстремальная волна”).

Здесь волна-убийца ударила в корпус корабля. А вот результат другого события: волна прошла под танкером и подняла его. В тот момент, когда корабль был поднят, он опирался на одну точку. Танкер на это не рассчитан и переломился пополам под собственным весом.

Как построить теорию этих волн? Этой теорией мы начали заниматься, когда уже накопили очень большой опыт работы с экстремальными волнами других типов (т.е. самофокусировка волн, ленгмюровский коллапс). Тогда уже было ясно, что появление таких волн должно быть связано с неустойчивостью монохроматических волн. Действительно, так и случилось. Есть такое точное решение в гидродинамике, которое называется “волна Стокса”. Оно было известно Стоксу еще в середине ХIХ века. Эта волна неустойчива. Тем не менее, эту неустойчивость можно промоделировать, но придется решать точное уравнение гидродинамики, потому что приближенные модели, увы, не работают, поскольку у нас нет никакого малого параметра. Однако же можно, исхитрившись, применив конформные преобразования, получить довольно простую систему уравнений, которая решается. Скажем, если мы зададим в качестве начального условия волну Стокса (здесь у нее около 100 периодов слегка промодулировано), пройдет некоторое время, и она выдаст вам вот такую волну.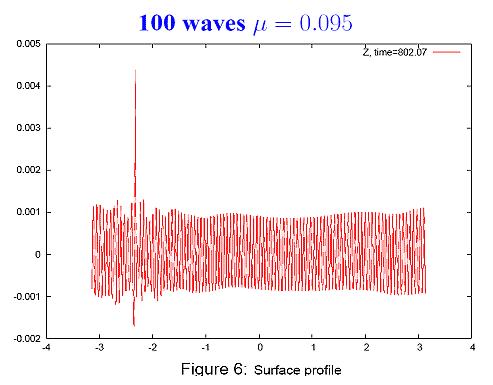

Вот эта волна более крупным планом. Видно, что волна хочет опрокинуться, и она опрокинется.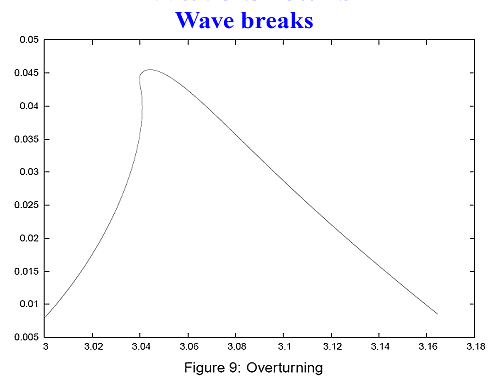

Дальше мы не считали, потому что компьютер отказал. Считалось это при помощи кода Фурье. В этот момент у нас было 2 миллиона гармоник, и дальше наш маленький компьютер не справлялся. На Крее можно было бы сделать 10 миллионов гармоник, и мы бы увидели тогда волну, имеющую форму волны на известной картине Хокусаи.

Вот эта картинка важная. К сожалению, здесь плохо видно зеленый максимум. Это распределение плотности продольного импульса в разные моменты времени: вот в начале, когда волна только развивается, тут она уже поближе развилась, а это максимум (не знаю, насколько хорошо его видно). На корабль идет водяная стенка, и, когда она по нему ударит, этот поток импульса превратится в давление, поэтому неудивительно, что эти волны всё разрушают.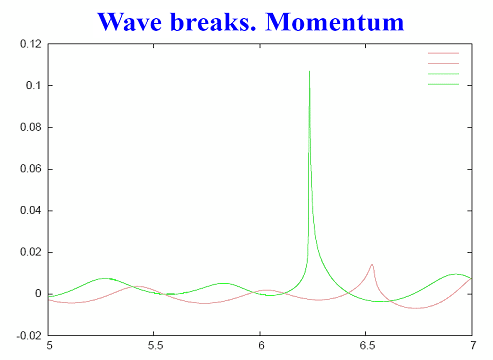

Оказывается, что если мы все-таки создадим волну, где имеются малые параметры, то есть пустим слабо промодулированный пакет, то нелинейное уравнение Шредингера (как я говорил, это универсальная модель) будет работать и здесь. Тогда ничего особенного не получится: будет солитон, который станет распространяться в зависимости от крутизны.

Теперь я хочу показать еще один фильм. Все определяется тем, насколько сильна нелинейность. В линейной теории, как известно, ничего не происходит. Все определяется степенью крутизны. Та картинка, которую я показывал, имеет крутизну 0,07, а эта вот 0,14. Как вы видите, крутизна 0,14 выдает уже образование настоящих freak-waves. (videoclip: 5Sol_Steep-0.14)

В этом деле поразительно, что достаточно часто freak-waves возникают, а потом собираются обратно. Этот процесс повторяется периодически. Такое поведение бывает у интегрируемых систем. Как я говорил, нелинейность Шредингера интегрируема, но если эта система интегрируема, то каким-то совершенно неведомым нам способом, потому что те приемчики, которые разработаны в теории интегрируемых систем за последние, наверное, лет 40, точно не работают. Тем не менее, поведение видите какое — регулярное, правильное. Эти волны — одиночные. Это уравнение гидродинамики мы точно решали, и я хочу подчеркнуть, что здесь никаких приближений не было сделано. Интегрируемость уравнения гидродинамики на глубокой воде — чрезвычайно волнующая загадка и вызов для аналитика, но в данном случае я выражаю вполне определенный оптимизм: я думаю, что довольно скоро положительное решение этой проблемы будет предъявлено. Пока же только скажу, что подержимся за дерево. Всё.

Обсуждение лекции

Борис Долгин: Может быть, стоит ввести некоторые понятия из тех, что употреблялись сегодня вами? Например, понятие интегрируемой системы.

Владимир Захаров (фото Наташи Четвериковой)

Владимир Захаров: Рассмотрим движение предмета произвольной формы в пустом пространстве. Тот факт, что он находится в поле тяжести, не имеет значения, поскольку мы перейдем в систему, движущуюся с центром массы. Решение дается аналитически и выражается в эллиптических функциях. Это — интегрируемая система.

Если я возьму такие же очки, предположим, закреплю это в одной точке и дам возможность как угодно крутиться, то окажется, что я не смогу в общем случае аналитически описать эту задачу. Но имеются отдельные случаи: если форма очков будет весьма специальная и закреплены они будут в определенной точке, то есть два случая, когда система интегрируема. Один из них нашла Ковалевская, это так называемый “волчок Ковалевской”. Весь ХIХ век математики буквально головой бились, пытаясь решить эту задачу и проинтегрировать общее уравнение, описывающее волчок с закрепленной точкой, пока наконец Пуанкаре (чье имя уже звучало) не показал, что это сделать нельзя, и не доказал его неинтегрируемость. Он говорил: “Ну, возьмем волчок Ковалевской и немного деформируем его”. У волчка Ковалевской есть лишний интеграл движения по сравнению с имеющимися интегралами. Оказывается, если мы немножко деформируем волчок, изменим соотношение между моментами инерции и попытаемся построить этот интеграл в виде ряда по отклонению от этой малой деформации, то члены ряда будут расходиться, они будут иметь так называемые малые знаменатели. Они будут обращаться в бесконечность — и интеграл разрушится.

Интегрируемые системы — те, что интегрируются в квадратурах, — в механике чрезвычайно большая редкость. На самом деле, есть точное определение интегрируемых систем, данное Лиувиллем. Сейчас это называется теоремой Лиувилля (иногда “теорема Лиувилля-Арнольда”) о том, что если имеем систему с n степенями свободы, то описывающая ее система 2n дифференциальных уравнений первого порядка должна иметь n интегралов движения, сохраняющихся величин. Более того, они еще должны порождать так называемую абелеву группу, то есть подчиняться некоторым специальным требованиям. Только тогда это — интегрируемая система.

До недавнего времени, скажем, до середины 60-х годов, было известно лишь очень небольшое число интегрируемых систем. Среди них свободное движение частиц, разумеется, система линейных осцилляторов. Нелинейные системы такие: движение в центрально-симетричном поле, движение в поле двух кулоновских центров и задачи динамики твердого тела, известные еще с ХIХ века.

Если бы мои очки были аксиально симметричны, карандаш такой, тогда это была бы интегрируемая система. Это установил Лагранж еще в ХVIII веке.

Каждый класс интегрируемых систем порождает целую науку систем, близких к интегрируемым. Для этого развивается теория возмущений, на которой держится три четверти теоретической физики. Например, система нелинейных осцилляторов, грубо говоря, порождает квантовую теорию поля и физику твердого тела. Система движения в поле двух кулоновских центров порождает небесную механику. Движение в центрально-симметричном поле порождает атомную физику. В атомной физике интегралом движения является полный момент М и L — проекция момента M на любую заданную ось.

Пуанкаре показал, что если взять интегрируемую систему и немного деформировать ее, то получится уже система неинтегрируемая, лишние интегралы исчезнут, их нельзя будет построить, они будут даваться расходящимися рядами. Впоследствии Арнольд и Колмогоров создали так называемую КАМ (Колмогоров, Арнольд и Мозер) — теорию, в которой они доказали, что даже неинтегрируемые системы ведут себя частично как интегрируемые, если они к ним близки. Там есть зоны, где интегралы разрушаются, а есть зоны, где их можно сохранить.

В 1967 году возникла работа Крускала, Гарднера, Грина и Миуры, в которой было показано, что некое давно уже известное уравнение Кортевега-де Фриса имеет точное решение в элементарных функциях, которого от него никто не ждал. Через некоторое время мы с Фаддеевым (Людвиг Дмитриевич Фаддеев — известный математик) поняли, что это — новый класс интегрируемых систем. В 1971 году вышла наша статья, которая стала довольно известной.

Вторым примером таких интегрируемых систем было нелинейное уравнение Шредингера, по которому выяснилось, что существует множество неизвестных ранее интегрируемых систем (сейчас, я думаю, счет идет на сотни, уже есть сотни две, может быть). Я даже не знаю их все и ориентируюсь примерно: это к такому классу относится, а это к такому. Запомнить это трудно: их действительно много и далеко не все из них имеют физическое применение.

Эта наука развивалась и продолжает развиваться, устраиваются конференции. Оказалось, что она очень сильно помогла классической математике в решении целого ряда чисто математических, в том числе геометрических задач.

Кстати, интересно, как возникла работа недавно скончавшегося Крускала (Martin David Kruscal, 1925-2006) и его соавторов. Крускал был великий по потенциалу ученый. Когда появились большие компьютеры, то возникла идея проверить обоснование статистической механики: взять какую-нибудь систему уравнений, описывающую физическую, гамильтонову систему, сохраняющуюся без диссипации, посчитать ее на компьютере и убедиться, что происходит термализация, возникновение статистического ансамбля, как полагается по законам термодинамики. Считается, что любые большие системы действительно быстро приходят в состояние термодинамического равновесия.

Была взята система шариков, соединенных между собой цепочками. Сделали это Ферми, Паста и Улам в 1954 году, как только появились первые компьютеры, в Принстоне, в институте, где тогда еще был фон Нейман, который, собственно, и руководил созданием первых компьютеров. Машина (кажется, она называлась ENIAC, у нее было весьма экзотическое название) тогда была суперкомпьютером, занимавшим здоровенное здание (оно до сих пор сохранилось около Института высших исследований и теперь представляет собой, разумеется, музей). Мощность этого компьютера, наверное, составляет 1% от того ноутбука, который я сейчас использую. Я грубо оцениваю, но мой компьютер как минимум в 100 раз мощнее. Они посчитали и построили систему: взяли 64 шарика, соединенных нелинейными пружинками, пустили их и стали надеяться, что очень быстро все шарики придут в термодинамическое равновесие, возникнет некая температура. Оказалось, ничего подобного. Шарики вели себя очень регулярно, они собирались, образовывали кластер, потом растекались обратно и т.д. И сколько они ни считали, они не могли достичь термодинамического равновесия. Это был шок, парадокс. Так называемая “проблема Ферми-Паста-Улама”.

Ферми сам занимался этим. Он-то был убежден, что термодинамическое равновесие наступит быстро. Выдвигались всякие достаточно экзотические объяснения, но все оказались неверными. В конце концов оказалось, что система — та система, которая есть, которую они использовали, — на самом деле близка к интегрируемой, но не совсем интегрируемая при тех уровнях, которые у них были. А интегрируемые системы не приходят в состояние термодинамического равновесия, потому что у них есть дополнительные интегралы движения. У обычных систем все определяется только энергией, так как с ней связана температура. А интегрируемых систем бесконечное число: сколько интегралов, столько и степеней свободы, поэтому они не приходят в термодинамическое равновесие, точнее, у них есть бесконечно много термодинамических равновесий, соответствующих каждому заданному набору интегралов, но и к ним надо тоже подойти. Короче говоря, это был парадокс, и он разрешился постепенно благодаря тому, что потом была найдена некая модель, описывающая достаточно точно цепочку этой системы шариков, более простая и изящная математически. И эта модель была точно решена. Потом мы установили, что эта модель интегрируемая.

Я должен сказать, что хорошо все это помню: это происходило на моих глазах. Когда пришла работа Крускала, опубликованная в “Physical Review Letters”, я уже был кандидатом наук и работал в Институте ядерной физики вместе с Эдуардом Павловичем Кругляковым (мы с ним старые друзья). Мы были совершенно ошеломлены этой работой, мы понимали, что коснулись чего-то совершенно замечательного и великого. Но что это? Это выглядело как невероятная загадка. Потом в Академгородок приехал великий математик Питер Лакс из Нью-Йоркского Института Куранта, ныне здравствующий, получивший недавно премию Абеля, аналог Нобелевской премии у математиков. Заметим, что медаль Филдса дают только молодым. Он привез нам некую интерпретацию (ту же самую работу, просто она была изложена на другом языке, гораздо более простом и понятном), и тогда возникли соображения, что существуют другие интегрируемые системы. И мы с Алексеем Борисовичем Шабатом установили интегрируемую систему Шредингера. Семен Львович Мушер, присутствующий здесь, наверное, хорошо помнит это время: он был моим аспирантом.

Голос из зала: Славные времена.

Владимир Захаров: Славны те героические времена. Сейчас ясно, что интегрируемых систем очень много, и все время открываются новые классы. Как и раньше, очень большую роль играют численные эксперименты. С проблемой Ферми-Паста-Улан вся эта теория продвинулась в своем развитии. До этого она стояла на месте: уравнение Кортевега-де Фриса было написано в 1895 году. Факт существования у него солитонных решений был установлен раньше, это сделал еще Буссинеск в 70-е годы ХIХ века. Оно лежало мертвым грузом, пока не понадобилось для этой системы. Толчок дал численный эксперимент. Поэтому до сих пор численный эксперимент (и лабораторный, конечно, тоже) дают пищу для размышлений и бросают вызовы. То уравнение, которое я показывал вам для солитона с крутизной 14%, — это совершенно типичное поведение интегрируемой системы: она ведет себя регулярно, она бывает периодична. Возникают какие-то такие страшные пики, и потом все повторяется снова. Так обменивается энергия. Но как построить? Имеющиеся методы очевидным образом не работают, это сразу можно сказать.

Константин Иванович: Я хотел бы уточнить. Вы показывали вид волны-убийцы со спутника. Это выглядит как столб, который движется, или как катер, который оставляет за собой треугольный хвост? Это один вопрос.

Второй вопрос: теорема Ферма — она считается решенной математиками или нет?

Владимир Захаров: Да, она решена, безусловно. Но это не имеет абсолютно никакого отношения к предмету нашего исследования: это теория чисел и, в общем, это совсем не моя область. Если я еще в состоянии разобраться в работе Перельмана, то для того, что я собираюсь сделать (будущей весной я буду читать общий курс по теории относительности), я уже купил книжку по потокам Риччи, обязательно разберусь, хотя это будет большой труд: наверное, страниц 200 придется прочитать. Но чтобы разобраться в доказательстве теоремы Ферма, мне пришлось бы, наверное, потратить не меньше полугода и все остальные дела отложить в сторону.

Она действительно доказана. Доказал это Эндрю Вайлз (Andrew Wiles), математик из Принстона. Интересно, что доказательство оказалось достаточно неожиданным. Полная противоположность тому, что было в случае с Перельманом, потому что там направление было понятным. Это как восхождение на очень сложную вершину — то, что сделал Перельман, никому до него не удавалось сделать. Вот — стоит стена, и на нее нужно залезть.

А там был найден неожиданный обходной путь. Совершенно неожиданный: никто не знал, что так можно подойти. Способ, которым была решена теорема Ферма, применим лишь для небольшого класса уравнений. Там тоже была драматическая история. Вначале Вайлз сделал свое доказательство, но в нем были ошибки, ему их указали, и он сам же их исправил.

Я не занимаюсь теорией чисел, но как раз в этой области специалистов очень много. Желающих доказать теорему Ферма было сколько угодно, потому мгновенно разобрались в ее доказательстве, нашли у Вайлза ошибки. Когда это происходило, Институтом Клея еще не было объявлено 10 проблем, а то он, конечно, получил бы свой миллион. Тем не менее, какую-то крупную премию из частного фонда ему дали. Кажется, это был фонд Слоуна ("Полит.ру" - Wolfskehl prize). Я видел его руководителя: высокий, очень симпатичный скромный человек, блондин, я бы даже сказал, альбинос.

Борис Долгин: Первый вопрос был относительно формы волны.

Владимир Захаров: Давайте просто посмотрим ее еще раз. Вот видите это светлое пятнышко? Это и есть волна. Она одномерная.

Константин Иванович: Типа катера.

Владимир Захаров: Ну что значит типа катера? Это такая волна, бегущая в одном направлении (как то, что мы видим), слегка модулированная в перпендикулярном направлении.

Борис Долгин: То есть она тут движется слева направо?

Владимир Захаров: Вот сюда она движется, в этом направлении. Вот в этом месте у нее гребень, он сильно вытянут в этом направлении и приблизительно раз в 5 шире. А вот это — его срез в заданном направлении. Спутник сканирует и снимает высоту поверхности. Он сделал срез в точности по этой прямой. Вот такая волна.

Очень интересный вопрос, кстати говоря, в связи с этой теорией. Иногда такие волны обрушаются, но далеко не всегда так, как мы видели, потому что мы решали точное уравнение. Она может возникнуть, а потом энергия снова вернется в волновое поле. В уравнении Шредингера такое решение известно: гомоклиническое решение было найдено Перегрином в 1983 году. Также один из моих учеников — Евгений Александрович Кузнецов — нашел решение, описывающее такие периодические волны, возникающие и исчезающие. Но это только для нелинейного уравнения Шредингера, что непригодно для этой задачи. Но то, что такое же поведение демонстрирует точное уравнение, есть, конечно, просто вызов лично мне как специалисту по интегрируемым системам.

Олег Градов, биохимик: Вы указали на существование солитонов при самофокусировке. Недавно вышел под редакцией Ахмедиева и Анкевича сборник статей по диссипативным солитонам. В связи с этим у меня комплексный, так сказать, вопрос. Если существуют диссипативные солитоны, можно ли рассматривать самофокусировку как самоорганизацию (вы говорили, как квазилинзу), и возможна ли самоорганизация в фокусе линзы уже материальных структур, то есть не оптическая, а солитонов подобного рода?

Владимир Захаров: Вполне законный вопрос. Нет, конечно, существуют диссипативные солитоны.

Борис Долгин: Владимир Евгеньевич, введите понятие диссипативных солитонов.

Владимир Захаров (фото Наташи Четвериковой)

Владимир Захаров: Если бы у уравнения Риччи решения не взрывались (а они взрываются), а стремились бы к некоторому пределу, это был бы диссипативный солитон, потому что это — уравнение типа уравнения теплопроводности, а не гамильтоново. Такие конструкции бывают. Есть сколько угодно таких примеров, когда вы пишете диссипативное уравнение с нелинейностью — и оно формирует определенную структуру. Эта структура бывает устойчивой. Наиболее известная из них — так называемое уравнение Курамото-Сивашинского. Такие системы описывают то, что возникает в пламени: возникают либо стационарные формы, либо бегущие. Вообще, конечно, представим себе свечу (есть такой диссипативный солитон — что ходить далеко за примерами). В ней происходит процесс горения и излучения энергии, и это, конечно, не консервативная система. Тем не менее, у нее есть определенные устойчивые структуры: если вы подуете на пламя, оно покачается и потом вернется обратно. Вот это и будет диссипативный солитон.

Свечек такого рода существует сколько угодно. Насколько это применимо к формированию? Думаю, что формирование кристаллов так и происходит, это же тоже диссипативный процесс: подлетают атомы, садятся, упорядочиваются, выбрасывают лишнюю энергию, и возникает структура. Да, конечно, именно самоорганизация в таких системах возможна. Вы можете специально подумать, как устроить такую хитрую самоорганизацию. Очень красивый пример самоорганизации (правда, это не в солитоне, а в периодической структуре) возникает при конвекции. Если вы имеете, предположим, нагретую поверхность (вот, скажем, пустыня Сахара), солнце греет песок, а в атмосфере возникают шестиугольные структуры (так называемые “ячейки Бенара”). Конвекция — очень интересная наука. В ней сейчас сделаны тончайшие эксперименты по возникновению разного рода структур. Действительно, это самоорганизующиеся структуры. Их множество. Например, кора на деревьях.

Олег Градов: Вопрос состоял несколько в ином плане: можно ли рассматривать самофокусировку как подобное явление?

Владимир Захаров: Это вопрос терминологический. Естественно, чтобы получить устойчивую структуру, вы должны немножко испортить нелинейность Шредингера, вы должны добавить туда диссипативные члены.

Вот нелинейное уравнение Шредингера. Оно наложено на комплексную функцию, но имеет вещественные коэффициенты. Теперь представьте себе, что эти коэффициенты комплексные, невещественные. Здесь у вас будет, предположим, затухание (в зависимости от знака они будут выдавать либо затухание, либо неустойчивость). Можете еще в нелинейность комплексность добавить.

Олег Градов: Тогда частоту нельзя убрать, если перед ней комплексный член стоит.

Владимир Захаров: Правильно. И вы получите то, что называется “уравнение Гинзбурга-Ландау”. У него есть множество разных структур. Если эти мнимые части ваших коэффициентов малы, то, действительно, это близко к самофокусировке. Но это уже другая наука. Конечно, там не будет коллапса настоящего. Эта вот штука остановится. Мы видели в тех экспериментах, которые были предъявлены, что там решались именно такие, исправленные уравнения, потому что иначе точное уравнение невозможно решить: нельзя получить бесконечность в реальном счете, надо как-то ограничиться.

Вот что интересно: в двухмерном уравнении Шредингера не возникает структур, и если вы дополнительно добавите нелинейную мнимую часть в затухании, там возникнет и исчезнет коллапс. Грубо говоря, она у вас поведет себя так, а потом вернется обратно, до нуля. Но в трехмерии и четырехмерии уже будут возникать структуры — так называемые “долгоживущие фокусы”.

Вот что произойдет в трехмерии. Максимум будет таким, потом выйдет на константу и останется вот так стоять. Это будет такая горячая точка, которая станет поглощать энергию из окружающей среды, наподобие того, как черная дыра поглощает пыль из космоса. Если вы хотите назвать это самоорганизацией, это приемлемо. Но такая штука живет, пока ее подпитывает энергия, так же, как свеча живет, пока есть, чему гореть. Могут ли возникать такие структуры в результате самофокусировки? В трехмерии да, в двухмерии нет.

Олег Градов: Спасибо.

Вопрос из зала: Поскольку я не физик и давно уже не математик, поэтому несколько упрощенно. Первое, я хотел бы уточнить: нелинейности двух типов образуются в самом уравнении и в граничных условиях. Правильно я понимаю эту часть?

Владимир Захаров: Граничные условия я не обсуждал.

Вопрос из зала: Я имею в виду в принципе.

Владимир Захаров: А, ну конечно, граничные условия важны, и любой численный эксперимент можно произвести только в ограниченной системе, в бесконечной это невозможно. Граничные условия несколько усложняют дело с точки зрения математики, но в принципе на интегрируемость они не влияют. Ну, конечно, вы можете придумать такие граничные условия, при которых вы потеряете интегрируемость, — скажем, поставить поглощение на границе. Если граничные условия разумны, то они принципиально дела не меняют.

Вопрос из зала: Дальше несколько простых вопросов. Я понял из такого довольно популярного изложения, что гипотеза Пуанкаре оказалась трудной для трехмерного пространства.

Владимир Захаров: Для высших размерностей она уже давно доказана.

Вопрос из зала: Как объяснить этот феномен с точки зрения нелинейности, если тут подходит нечто.

Владимир Захаров: Вы знаете, я боюсь, что не могу ответить на этот вопрос. Для этого надо действительно сесть и подробно разобрать работу Перельмана, а это нелегкий труд.

Вопрос из зала: Ну, я невозможного не прошу. Последний вопрос из этой же серии. В качественных решениях нелинейных уравнений, о которых я слушал лекции супруги академика Леонтовича в Нижнем Новгороде (я сам учился в Горьковском университете), были развитые подходы (тоже численные, по-видимому, хотя назывались качественными), и там возникало понятие точек бифуркации. Есть ли какая-то связь с этими фокусами и саморазжиганиями многочисленных поверхностей? Какие-то корреляции, я имею в виду. Спасибо.

Владимир Захаров: Понимаете, понятие точек бифуркации обычно применяется к диссипативным системам. Какой бы привести пример точки бифуркации? Предположим, у вас имеется течение вязкой жидкости между двумя цилиндрами. Внешний цилиндр неподвижен, а внутренний цилиндр вращается. Дальше о скорости вращения этого внутреннего цилиндра. Если скорость вращения маленькая, то устанавливается так называемое “течение Куэтта” — и все нормально. Если внутренний цилиндр вращается достаточно быстро, в какой-то момент она становится неустойчивой. Вот это и есть точка бифуркации по параметру, который есть скорость вращения или число Рейнольдса, что почти одно и то же в данном случае. Вот вы прошли точку бифуркации, оказывается, что течение перестает быть однородным, и возникает вертикальная структура вихрей, которая будет периодически расположена вдоль вертикальной оси. Это еще можно описать.

Если вы дальше увеличиваете скорость вращения, у вас будет следующая точка бифуркации, а после нее наступит хаос, система будет стремиться к странному аттрактору, ее поведение будет уже неописываемо. Но даже это не означает, что вы достигли полной универсальности. Вы еще увеличиваете скорость вращения, снова возникает точка бифуркации, один тип хаоса сменяет другой тип хаоса, изменяется размер странного аттрактора и т.д. По мере того, как вы увеличиваете скорость вращения, у вас будет бесконечное число точек бифуркации. В конце концов вы придете к состоянию развитой турбулентности. Точка бифуркации — это как две диссипативных системы, зависящих от параметров (в данном случае параметром является скорость вращения). На прямой, по которой отложен параметр, есть точки, в которых происходит смена типа поведения системы. Вот это и есть точки бифуркации.

В динамических, в гамильтоновых системах такого не бывает, потому что там все зависит от начальных условий. В диссипативных системах поведение, асимптотическое по времени, не зависит от начальных условий. При данной скорости внутреннего вращения, какое бы вы условие ни задали, система о нем через некоторое время забывает, она будет вести себя так, как ей положено при данной скорости вращения. В системах интегрируемых система помнит вечно, что с ней было в начале, и там не может быть такого. Там тоже могут быть разные режимы, но они зависят от начальных условий.

Вопрос из зала: Я бы хотела спросить об экстремальных волнах в океане, о гипотезах. Сейчас не существует теории, однозначно описывающей и объясняющей эти волны, а гипотезы есть. Так? Хотелось бы услышать пару гипотез и подробнее узнать про гипотезу о блуждающих черных дырах.

Владимир Захаров: Начну с блуждающих черных дыр. Это действительно очень интересный вопрос. Дело в том, что, когда наша вселенная создавалась, произошел большой взрыв, было создано много черных дыр — сгустков материи, которые коллапсировали в черные дыры. Судьба этих черных дыр зависит от масс. Если масса черной дыры не очень велика, то черная дыра испаряется, исчезает, взрывается, потому что происходит такой процесс: вблизи черной дыры из вакуума рождаются пары электрон-позитрон (частица и античастица). Черная дыра эти античастицы поглощает, и они уменьшают ее массу в результате. Постепенно она взрывается. Испарение черных дыр придумал знаменитый Хокинг.

Чем больше у черной дыры масса, тем медленнее она испаряется. До нашего времени дожили, могут дожить черные дыры с массой порядка 10 в пятнадцатой степени тонн (тысяча триллионов). Это масса хорошей горы, которая, однако же, сосредоточена в размере — я сейчас так быстро не могу сосчитать — чрезвычайно маленьком, меньше электрона, конечно). Эта черная дыра может идти, блуждать со скоростью, довольно близкой скорости света. Скорость у нее примерно такая же, как у нас по отношению к горизонту.

Чрезвычайно подробно изучался вопрос о том, что будет, если такая дыра пролетит через Землю. На своем пути она, конечно, все уничтожит. В любом твердом веществе она проделает дыру, канал диаметром примерно сантиметров 5. Внутри канала она все выжжет, и то, что было внутри канала, превратится в пар, в плазму, а дальше будет вести себя так же, как ведет себя в таких случаях горная порода. Можно где-нибудь в скалах (это уже вопрос к геологам) найти следы прохождения черных дыр, но пока их не нашли.

Другая идея состоит в том, что когда она летит через океан, через воду, то поскольку она летит с очень большой скоростью, должно происходить черенковское излучение: она должна излучать звук. В принципе, можно было бы представить себе датчики — известно, каким будет спектр этого звука, волны будут довольно длинными. Только, конечно, нужно построить программу по систематическому поиску таких сигналов. Подсчитывали — это очень дорогое удовольствие, и непонятно, какой от этого практический толк, потому что дыра сама, поскольку у нее масса чудовищная при том, что она очень маленькая (ей что через Землю лететь, что через вакуум — совершенно никакой разницы нет), не чувствует этого, для нее наша Земля совершенно не преграда.

Но такое вот изучают, есть исследования по возможности фиксирования существования черных дыр. Наиболее перспективные — по звуку, который они возбудили. Но дальше разговоров дело не пошло. Значит, это второй вопрос. А первый был у вас о чем?

Борис Долгин: О гипотезах про волны.

Владимир Захаров: Высказывалось множество разных идей о возникновении волн-убийц. По-видимому, большинство из них неправильные. Например, идея, что это связано с конечностью глубины, с обрушением волн на конечной глубине. На самом деле волны-убийцы наблюдаются в глубоком океане. Это очень естественное явление, если достаточно долго подождать, более или менее из любого спектра должна возникнуть такая freak-wave. Недавно мы делали эксперименты, провели 5 тысяч расчетов, и с хорошей вероятностью видели ее во всех случаях. В зависимости от ширины спектра вероятность могла быть довольно маленькой, но все-таки не нулевая.

Не случайно я начал свою лекцию с того, что показал вам совсем тривиальную вещь, которую все знают, а именно обычную фокусировку при помощи линзы. Оказывается, что такого рода линейная фокусировка тоже играет роль в создании волн-убийц. В мире есть районы, где волны-убийцы наблюдаются гораздо чаще, чем в других местах. Самое неприятное место, имеющее наиболее плохую репутацию, — так называемое Agulhas current, это юго-восток Африки. Если представить себе Африку: самый юг — Кейптаун, мыс Доброй надежды, и оттуда на северо-восток вдоль побережья.

Голос из зала: У пиратов?

Владимир Захаров: Ну, пиратский берег, он на западной стороне Африки, там, где пустыня (не помню, как она называется). А на северо-востоке, там, где город Дурбан, вдоль побережья имеется океанское течение, называется Agulhas current (“current” — “поток”). Течение довольно быстрое, что-то вроде 5 миль/час, 8 км/ч на юг. Капитаны любят использовать это место для того, чтобы экономить горючее и получать за это премию. Но, к сожалению, получается так, что достаточно часто они там встречаются с волнами-убийцами. С точки зрения волн-убийц это место — самое худшее на всем земном шаре, хотя волны-убийцы бывают, как вы видели, и около Швеции, и в Марселе.

Почему так? Это имеет вполне рациональное объяснение. Дело в том, что далеко к югу от Африки расположена Антарктида, а между ними сплошной океан, опоясывающий весь земной шар. И в этом океане постоянно происходят штормы на 40-х широтах — так уж там все устроено, что “ревущие сороковые” есть и на севере, и на юге. В этих “ревущих сороковых” происходят штормы, а от штормов происходит зыбь, которая непрерывно распространяется на север, и она очень далеко идет — волны мало затухают, и такая волна может обогнуть весь земной шар несколько раз без затухания. Дальше волны натыкаются на это течение. Оно, конечно, неоднородно, его скорость зависит от расстояния до берега. Поэтому траектория лучей изгибается. Вот видите, здесь прямая траектория лучей изогнулась. Если бы здесь была хаотическая линза, не такая хорошая, траектории лучей изгибались бы достаточно случайным образом. Но все равно были бы такие точки, где лучи касались друг друга. Вот, например, когда вы смотрите в стакан с чаем при солнечном свете, вы видите там яркие линии, они называются каустики.

Собственно говоря, течение Agulhas current играет роль системы линз для волн, бегущих со стороны Антарктики. Фокусы эти плохие, они размазаны на 100 километров, к примеру, но все-таки 100 километров не так уж много (или, может быть, немножко меньше 100). В этих фокусах амплитуда волн возрастает, происходит концентрация энергии, и она служит триггером для появления freak-waves, у которых пороговый эффект очень сильно зависит от исходной амплитуды.

Группа математиков из университета Боулдер в штате Колорадо, где провел последние годы жизни великий Гамов (он выдвинул теорию “горячей вселенной”, а также вложил вклад в расшифровку генетического кода), произвела численные расчеты траектории лучей волн, идущих из Антарктики. Распределение скорости течения как функции от расстояния уже давно проверено с очень хорошей точностью, поэтому ученые знают, как это течение устроено. Они посчитали, нашли эти каустики, и потом возникла система пятен. После чего они связались с компанией Ллойда (“Регистр Ллойда”), которая занимается тем, что собирает сведения обо всех кораблекрушениях, которые происходят в мире, и сравнили статистику кораблекрушений. Оказалось, что крушения как раз происходили в тех местах, где происходит фокусировка (сначала линейная, потом уж нелинейная) этих океанских волн. Там, между прочим, до изобретения радио, вообще происходило Бог знает что: гибли пассажирские лайнеры.

Вопрос из зала: А старты подводных НЛО — чушь абсолютная?

Борис Долгин: Я боюсь, про НЛО — это не к нам.

Вопрос из зала: У меня два простых вопроса. Первый, может быть, не имеет прямого отношения к нашей теме, но очень хочется спросить про мост в Волгограде. Когда этот вопрос обсуждался в Думе, депутат-физик Иван Грачев сказал: “Ну, чисто учебник физики: стоячая волна наблюдается”.

Владимир Захаров: Я не знаю эту историю.

Вопрос из зала (продолжение): Достаточно видеть кадры по телевидению.

Борис Долгин: Там некий недавно построенный мост, после воздействия на который как будто бы обычного ветра, он вроде бы начал раскачиваться, но не разрушился при этом. Он стал вибрировать, но не деформироваться.

Владимир Захаров: Я, видимо, как-то оторвался от жизни и упустил эту информацию. Да, было что-то такое в средствах массовой информации. Но существует ведь классическая история — разрушение Такомского моста. Такома — это город в Америке севернее Сиэтла. Там был большой мост через залив, он разрушился, просто развалился. Почему? Это элементарная вещь, она представлена во всех учебниках физики. У каждой такой упругой системы есть собственные колебания, собственные частоты. В той или иной степени их пытаются придушить, сделать диссипативными, но не всегда это удается (может быть, это стоит денег, потому что утяжеляет конструкцию). Дальше, когда у вас имеется ветер, то там есть определенный спектр колебаний (так называемые “мезоскопические волны”), и если это попадет в резонанс, то дело закончится разрушением.

Вопрос из зала (продолжение): Главный мой вопрос касается того, до чего вы сами дошли. Гамов ведь не весь генетический код открыл — он только участвовал в этом. Мой вопрос про кору дерева. Существуют ли какие-то общие модели морфогенеза, индивидуального развития или развития в эволюции?

Владимир Захаров: Это все-таки не ко мне вопрос, тут надо к биологу обращаться. Я боюсь, что здесь моей эрудиции не хватит. Я только частично могу вам ответить. Вот сейчас построена математическая теория розы, цветков. Я слышал много докладов. Если вы посмотрите на цветок, то выясняется, что есть определенная закономерность того, как устроены эти лепестки, и где возникают новые. Там возникают числа Фибоначчи (когда следующее число составляется из суммы двух предыдущих). Сейчас есть целая наука о том, как возникают формы цветов. Строят модели роста цветов. Берут просто уравнения упругих пластин, к ним добавляются факторы роста; так, что пластины начинают сами раздуваться и находятся во взаимодействии друг с другом. Такая наука существует. Есть и этот морфогенез, если угодно. Могу назвать людей, которые этим занимаются — Алан Ньюэлл (Alan Newell), мой ближайший друг.

Есть очень интересные работы по росту деревьев, по появлению у них веток. Все это сейчас математически описывается, достаточно хорошо, между прочим.

Борис Долгин: Вообще, сейчас биологи — одни из основных потребителей математики.

Владимир Захаров: Это точно. Сейчас модно направление математической биологии.

Вопрос из зала: А в общественной жизни тоже?

Борис Долгин: Вот и последний вопрос — про общественную жизнь, видимо, про волны.

Владимир Захаров: Давно же экономисты занимаются, применяют теорию игр.

Борис Долгин: Наверное, речь шла про волны в общественной жизни?

Вопрос из зала: Про Кондратьева.

Владимир Захаров: Это циклы Кондратьева, а не волны.

06 октября 2010
Полит.ру