|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Закон Био — Савара |
Закон Био — Савара
Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.
Одним из величайших прорывов в естествознании XIX века стала серия открытий, позволивших установить неразрывную связь между двумя, казалось бы, не связанными между собой природными феноменами — электричеством и магнетизмом, — которые на поверку оказались просто двумя сторонами одной медали. Одним из первых фрагментов пазла, который предстояло собрать ученым, стало осознание того, что движущиеся электрические заряды (то есть электрический ток) могут порождать магнитное поле. Это открытие сделал датский ученый Ханс Кристиан Эрстед (см. открытие Эрстеда), а представил его в количественной форме французский ученый Андре-Мари Ампер (см. Закон Ампера). Обобщением этой работы стал закон Био—Савара (его еще называют «закон Био—Савара—Лапласа». — Прим. переводчика), содержащий окончательную формулировку соотношения между электрическими токами и магнитными полями, которые они производят. Жан Батист Био, яркий и смелый ученый, был профессором физики в Сорбонне и действительным членом французской Академии наук. Сразу после открытия Эрстеда вместе со своим коллегой Феликсом Саваром он принялся за изучение взаимосвязи между электрическим током и магнитными полями. В отличие от Ампера, изучавшего магнитные поля опосредованно, путем измерения силы взаимодействия между парами проводников с током, Био и Савар предприняли прямые измерения магнитных полей, используя для этого множество легких магнитных стрелок компасов. Смысл их закона проще всего понять, если представить себе, что проводник с током разбит на крошечные отрезки — т. н. элементы тока (такой подход предложил ученым их старший коллега Пьер Симон Лаплас (Pierre-Simon Laplace, 1749–1827), стоявший у истоков дифференциального и интегрального исчисления, который затем и обобщил полученные результаты. — Прим. переводчика). На каждом из этих крошечных отрезков кривизной проводника можно пренебречь — их можно рассматривать как отрезки прямой. Так вот, согласно закону Био—Савара, магнитное поле где Я уже упоминал, что закон Био—Савара является наиболее полным формальным обобщением взаимосвязи между электрическим током и магнитным полем. Это значит, что можно взять проводник с током сколь угодно сложной и асимметричной конфигурации и разбить его на элементы тока. Каждый элемент вносит свой вклад в магнитное поле в рассчитываемой точке. Сделав эти расчеты, мы можем затем просуммировать вклад от каждого элемента проводника и найти общее магнитное поле (этот процесс суммирования относится к области высшей математики и выглядит он достаточно сложно). Таким образом, закон Ампера является частным случаем закона Био—Савара для случая линейного проводника. Я еще не сказал, что закон Био—Савара предсказывает также направление получающегося магнитного поля. Это направление можно определить с помощью так называемого правила правой руки, ставшего настоящим бичом целых поколений студентов физических и технических вузов. Правило гласит: если вытянутый указательный палец правой руки показывает направление электрического тока в элементе тока, а средний палец направлен на точку, в которой вы вычисляете магнитное поле, то выставленный под прямым углом к двум другим пальцам большой палец укажет направление магнитного поля. Как я уже говорил, полное математическое выражение закона Био—Савара требует довольно сложных вычислений, поскольку оно представляет собой интегральное уравнение. Оно является, по сути, общим решением четвертого уравнения Максвелла. Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания». Джеймс Трефил — профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Закон Био — Савара |
|
[time: 11 ms; queries: 8]
22 Фев 2026 06:59:17 GMT+3 |


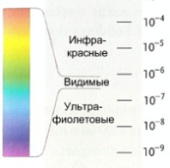 Имеется целый ряд типов электромагнитного излучения, начиная с радиоволн и заканчивая гамма-лучами. Электромагнитные лучи всех типов распространяются в вакууме со скоростью света и отличаются друг от друга только длинами волн.
Имеется целый ряд типов электромагнитного излучения, начиная с радиоволн и заканчивая гамма-лучами. Электромагнитные лучи всех типов распространяются в вакууме со скоростью света и отличаются друг от друга только длинами волн. Электродвигатель постоянного тока. Универсальный электродвигатель постоянного и переменного тока. Электродвигатель постоянного тока с тремя катушками. Бесщеточный электродвигатель постоянного тока. Шаговый электродвигатель. Асинхронный электродвигатель. Вращающееся магнитное поле и синхронная скорость. Однофазный асинхронный электродвигатель. Подключение по схеме «звезда» и «треугольник». Синхронный электродвигатель. Генератор переменного тока.
Электродвигатель постоянного тока. Универсальный электродвигатель постоянного и переменного тока. Электродвигатель постоянного тока с тремя катушками. Бесщеточный электродвигатель постоянного тока. Шаговый электродвигатель. Асинхронный электродвигатель. Вращающееся магнитное поле и синхронная скорость. Однофазный асинхронный электродвигатель. Подключение по схеме «звезда» и «треугольник». Синхронный электродвигатель. Генератор переменного тока.