Уравнения Максвелла

Все электромагнитные явления описываются системой из четырех уравнений.

К середине XIX века ученые открыли целый ряд законов, описывающих электрические и магнитные явления и связи между ними. В частности, были известны:

закон Кулона, описывающий силу взаимодействия между электрическими зарядами;
теорема Гаусса, исключающая возможность существования в природе изолированных магнитных зарядов (магнитных монополей);
закон Био—Савара, описывающий магнитные поля, возбуждаемые движущимися электрическими зарядами (см. также Закон Ампера);
законы электромагнитной индукции Фарадея, согласно которым изменение магнитного потока порождает электрическое поле и индуцирует ток в проводниках (см. также Правило Ленца).

Эти четыре группы законов и были обобщены Джеймсом Клерком Максвеллом, которому удалось объединить их в стройную систему (получившую его имя), состоящую из четырех уравнений и исчерпывающим образом описывающую все измеримые характеристики электромагнитных полей и электрических токов, которая названа его именем. Прежде всего, Максвеллу мы обязаны строгим математическим описанием всех известных законов электромагнетизма (Фарадей, например, вообще формулировал все открытые им законы исключительно в словесной форме). Во-вторых, в сформулированную им систему Максвелл внес немало принципиально новых идей, отсутствовавших в исходных законах. В-третьих, он придал всем электромагнитным явлениям строгое теоретическое обоснование. И, наконец, в-четвертых, на основе составленной им системы уравнений Максвелл сделал ряд важных предсказаний и открытий, включая предсказание существования спектра электромагнитного излучения.

Давайте начнем со второго пункта. Согласно закону Био—Савара, электрический ток, проходящий по проводнику, возбуждает вокруг него магнитное поле. А что если электрический ток протекает не по проводнику, а через плоский конденсатор? Фактически, электроны не перескакивают с одной пластины на другую, однако ток всё равно проходит через конденсатор, поскольку электроны одной пластины взаимодействуют с электронами другой пластины, находясь в непосредственной близости друг от друга, и, в силу взаимного отталкивания, передают друг другу колебания (так называемые осцилляции) переменного тока, обеспечивая, тем самым, протекание тока через, казалось бы, очевидный разрыв в электрической цепи.

Максвелл понял, что закон Ампера в этой ситуации не объясняет прохождение тока. Он также понял, что, хотя заряды с пластины на пластину не переходят, электрическое поле (сила, которая возникла бы, если бы мы поместили между пластинами воображаемый электрический заряд) увеличивается. Исходя из этого он постулировал, что в мире электромагнитных явлений изменяющееся электрическое поле может играть ту же роль в порождении магнитного поля, что и электрический ток. Максвелл ввел принципиально новое понятие тока смещения, добавив его в качестве отдельного слагаемого в обобщенный закон Ампера — первое уравнение Максвелла. И с тех пор наличие токов смещения раз за разом безоговорочно подтверждается экспериментальными данными.

Внеся столь важное дополнение в первое из четырех уравнений, Максвелл на основании составленной им системы уравнений чисто математически вывел фантастическое по тем временам предсказание: в природе должны существовать электромагнитные волны, формирующиеся в результате колебательного взаимодействия электрических и магнитных полей, и скорость их распространения должна быть пропорциональна силе между зарядами или между магнитами. Решив составленное им дифференциальное волновое уравнение, Максвелл с удивлением обнаружил, что скорость распространения электромагнитных колебаний совпадает со скоростью света, к тому времени уже определенной экспериментально. Это означало, что столь знакомое всем явление, как свет, представляет собой электромагнитные волны! Более того, Максвелл предсказал существование электромагнитных волн во всем известном спектре — от радиоволн до гамма-лучей. Таким образом, доскональное теоретическое исследование природы электричества и магнетизма привело к открытию, принесшему человечеству неисчислимые блага — от микроволновых печей до рентгеновских установок в стоматологических клиниках.

Уравнения Максвелла в дифференциальной форме

Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейным дифференциальным уравнениям в частных производных первого порядка для 12 компонент четырёх векторных функций $\mathbf {D} ,\;\mathbf {E} ,\;\mathbf {H} ,\;\mathbf {B}$ :

Название	Формула в системе СИ	Примерное словесное выражение
Закон Гаусса	$\nabla \cdot \mathbf {D} = \rho$	Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля	$\nabla \cdot \mathbf {B} = 0$	Не существует магнитных зарядов
Закон индукции Фарадея	$\nabla \times \mathbf {E} = -{\frac {\partial \mathbf {B} }{\partial t}}$	Изменение магнитной индукции порождает вихревое электрическое поле
Теорема о циркуляции магнитного поля	$\nabla \times \mathbf {H} = \mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}$	Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

$\rho$ — объёмная плотность стороннего электрического заряда;
$\mathbf {j}$ — плотность электрического тока (плотность тока проводимости);
$\mathbf {E}$ — напряжённость электрического поля;
$\mathbf {H}$ — напряжённость магнитного поля;
$\mathbf {D}$ — электрическая индукция;
$\mathbf {B}$ — магнитная индукция;
$\nabla$ — дифференциальный оператор набла, при этом:
$\nabla \times \mathbf {E} \equiv \mathrm {rot} \,\mathbf {E}$ означает ротор вектора,
$\nabla \cdot \mathbf {E} \equiv \mathrm {div} \,\mathbf {E}$ означает дивергенцию вектора.

Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле.

Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания».
Джеймс Трефил — профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.

Комментарии: 0

Похожее

Правило Ленца

Индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока.
Электромагнитные волны и уравнения Максвелла

Эмиль Ахмедов

Мой рассказ будет больше историческим: я расскажу о том, как возникла теория Максвелла и понятие электромагнитных волн. Были известны законы Кулона, закон Био — Савара, разные законы индукции Фарадея и другие. Этот набор экспериментальных данных Максвелл попытался описать теоретически. Насколько мне известно, его труд состоит из примерно шестисот страниц. Он пытался чисто механически объяснить законы Фарадея, описывая электромагнитное поле как набор шестеренок с разными сортами зацеплений. В XIX веке механическое описание природы было очень популярно. Большая часть этих шестисот страниц пропала, поскольку в них не было никаких конструктивных утверждений. Может, я немного преувеличиваю, но единственное конструктивное, что было в этом труде Максвелла, — это его уравнения, формулы.
Закон Био — Савара

Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.
Закон Ампера

Ханс Кристиан Эрстед экспериментально установил, что провод, по которому течет электрический ток, отклоняет магнитную стрелку компаса. Андре-Мари Ампер так заинтересовался этим явлением, что принялся за углубленное экспериментальное и математическое исследование взаимосвязи между электричеством и магнетизмом. В результате и был сформулирован закон: Движение электрических зарядов приводит к возникновению магнитных полей.
Закон Кулона

Сила взаимодействия между двумя точечными электрическими зарядами пропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния между ними. По своей математической форме он повторяет закон всемирного тяготения Ньютона, если заменить в последнем массы на заряды, а постоянную Ньютона, на постоянную Кулона. И для этого сходства есть все причины. Согласно современной квантовой теории поля и электрические, и гравитационные поля возникают, когда физические тела обмениваются между собой лишенными массы покоя элементарными частицами-энергоносителями — фотонами или гравитонами соответственно. Таким образом, несмотря на кажущееся различие в природе гравитации и электричества, у двух этих сил много общего.
Законы электромагнитной индукции Фарадея

Изменение магнитного потока, проходящего через площадь, приводит к возникновению электрического поля вдоль контура, ограничивающего эту площадь. Интенсивность этого электрического поля пропорциональна скорости изменения магнитного потока.
Теорема Гаусса о потоке напряженности электрического поля через замкнутую поверхность

Поток напряженности электрического поля, проходящий через замкнутую поверхность, пропорционален суммарному электрическому заряду, содержащемуся внутри этой поверхности.
Спектр электромагнитного излучения

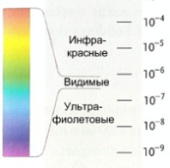Имеется целый ряд типов электромагнитного излучения, начиная с радиоволн и заканчивая гамма-лучами. Электромагнитные лучи всех типов распространяются в вакууме со скоростью света и отличаются друг от друга только длинами волн.
Никола Тесла: мифы и реальность

Ему приписывается знание будущего, способность получать энергию из вакуума и уничтожить Землю. На него даже возлагается вина за Тунгусскую катастрофу. О реальных работах Николы Тесла и о происхождении его мифа рассказал в интервью «Радио Свобода» Александр Костинский, кандидат физико-математических наук, специалист по физике газового разряда — области, близкой к работам Тесла.
Уравнения Максвелла, внешние дифференциальные формы и расслоения

Андрей Болибрух

В этих двух лекциях мы хотим рассказать вам о дифференциальных формах, расслоениях и связностях. Эти понятия сейчас активно используются в разных областях математики и физики, и нам хотелось бы хотя бы немного вас с ними познакомить. Для того чтобы наш рассказ не был излишне абстрактным, мы привязаться к такому физическому объекту, как электромагнитное поле, и показать вам как при попытке описания этого поля естественным путем возникают все перечисленные понятия.

Далее >>>

∀ x, y, z

Уравнения Максвелла

Теги

Похожее