|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ V. Нелогичное развитие логичнейшей из наук / Математика. Утрата определенности // Морис Клайн |
V. Нелогичное развитие логичнейшей из наук / Математика. Утрата определенностиМорис Клайн
V. Нелогичное развитие логичнейшей из наукНет, не оплакивать былое — Уордсворт
Что же открыло математикам глаза? Как они смогли понять, что заблуждались, полагаясь на безупречность математических рассуждений? Некоторые математики еще в начале XIX в. выражали озабоченность в связи с критикой, которой подвергались основные положения математического анализа, но большинство считало эти нападки недостаточно обоснованными и просто игнорировало их. Лишь появление неевклидовой геометрии и кватернионов, которые заставили математику отказаться от многовековых претензий на владение абсолютной истиной, побудило большинство математиков обратить внимание на пробелы в логике математических исследований. Работы в области неевклидовой геометрии, которые сопровождались постоянными и столь естественными ссылками на аналогичные теоремы и доказательства евклидовой геометрии, привели к поразительному открытию: выяснилось, что евклидова геометрия, которую на протяжении двух тысячелетий специалисты провозглашали неподражаемым образцом строгих доказательств, обладает серьезными логическими изъянами! Создание новых алгебр, начало которому было положено введением кватернионов (гл. IV), настолько обеспокоило математиков, что им захотелось подвергнуть критическому пересмотру логические основы арифметики и алгебры обычных вещественных и комплексных чисел. Такой пересмотр действительно был необходим — хотя бы для того, чтобы убедиться в надежности представлений о свойствах этих чисел. Открытие, которое ожидало математиков в, казалось бы, хорошо известной им области, было поистине удивительным: эти разделы математики, традиционно считавшиеся в высшей степени логичными, развивались алогично! Если хочешь разобраться в настоящем, следует прежде всего заглянуть в прошлое! Обратившись к прошлому, математики, чье восприятие обострилось в результате последних открытий, наконец увидели то, что ускользало от их предшественников или мимо чего те равнодушно проходили в своем безудержном стремлении постичь истину. Разумеется, математики отнюдь не собирались безропотно отказываться от своей науки. Помимо того что математические методы продолжали оставаться весьма эффективным инструментом естественнонаучного исследования, математика сама по себе превратилась в область знания, которую многие математики вслед за Платоном считали особой «внечувственной реальностью».{60} Естественно, математики сочли, что им под силу по крайней мере пересмотреть логическую структуру математики и восполнить пробелы в ней или изменить те ее области, где обнаружатся изъяны. Как нам уже известно, родоначальниками дедуктивной математики были древние греки и первым, казалось бы, совершенным математическим построением стали «Начала» Евклида. Начав с определений и аксиом, Евклид далее переходил к доказательству теорем. Повторим, однако, некоторые из определений Евклида:
1. Точка есть то, что не имеет частей. ([25], кн. I-VI, с. 11.) Аристотель учил, что определение должно описывать определяемое понятие через другие, уже известные понятия. А так как с чего-то необходимо начать, утверждал Аристотель, то в качестве исходных необходимо принять какие-то неопределяемые понятия. Хотя, судя по многим данным, Евклид, живший и работавший в Александрии примерно в III в. до н.э., хорошо знал о работах греческих авторов классической эпохи, в частности Аристотеля, он тем не менее дал определение всем геометрическим понятиям. Этот просчет Евклида принято объяснять двумя причинами. Либо Евклид был не согласен с Аристотелем в том, что исходные понятия должны быть неопределяемыми, либо, как утверждают некоторые защитники Евклида, он сознавал необходимость неопределяемых понятий, но своими первыми определениями намеревался дать лишь интуитивное представление о смысле определяемых понятий, позволяющее понять последующие аксиомы. Но если справедливо последнее, то в таком случае Евклид вряд ли стал бы включать определения в основной текст «Начал». Каковы бы ни были намерения самого Евклида, никто из математиков, следовавших дедуктивному методу Евклида на протяжении двух тысячелетий, не отметил необходимость неопределяемых понятий. На необходимость таких понятий обратил внимание в своем «Трактате о геометрическом духе» (1658) Паскаль, но это его напоминание просто не было никем замечено. А как обстояло дело с аксиомами Евклида? Следуя, по-видимому, Аристотелю, Евклид сформулировал ряд общих понятий, применимых к любому рассуждению, и пять постулатов, применимых только к геометрии. Одно из общих понятий гласило: «И если к равным [вещам] прибавляются равные, то и целые будут равны» ([25], кн. I-VI, с. 15). Под словом «вещи» Евклид понимал длины, площади, объемы и целые числа. Разумеется, это слово допускает весьма широкое толкование. Но еще в большей степени может вводить в заблуждение общее утверждение, что фигуры, совпадающие при наложении, равны. С помощью этой аксиомы Евклид доказывал конгруэнтность двух треугольников, налагая один треугольник на другой и выводя из известных геометрических фактов заключение о равенстве углов. Но чтобы наложить один треугольник на другой, его необходимо передвинуть. Евклид предполагал, что перемещение не сказывается на свойствах треугольника. Таким образом, общее понятие, задающее «принцип наложения», по существу, выражает однородность пространства, т.е. независимость свойств геометрических фигур от их расположения в пространстве. Такого рода допущение вполне разумно, но все же является дополнительным допущением: определения в евклидовых «Началах» не затрагивают понятия движения.{61} В своих доказательствах Евклид нередко прибегал к аксиомам, явно им не сформулированным. Еще Гаусс обратил внимание на то, что Евклид говорит о точках, лежащих между другими точками, и о прямых, лежащих между другими прямыми, ни словом не обмолвившись о понятии «лежать между» и его свойствах. По-видимому, Евклид мысленно представлял геометрические фигуры и использовал в доказательствах теорем свойства реальных фигур, не отраженные в аксиомах. Наглядные геометрические представления могут оказаться весьма полезными и при доказательстве, и при запоминании теоремы, но роль их должна быть лишь вспомогательной. Лейбниц обратил внимание еще на одну аксиому, неявно использованную Евклидом, — аксиому о так называемой непрерывности. Действительно, Евклид широко пользовался тем, что прямая, соединяющая точку A, расположенную по одну сторону от l (рис. 5.1), с точкой B, расположенной по другую сторону от прямой l, имеет с l общую точку. Существование общей точки очевидно из чертежа — однако ни одна аксиома о прямых не гарантирует, что такая общая точка действительно имеется. Впрочем, можно ли говорить, что точки «находятся по разные стороны от прямой»? Подобное словоупотребление также основывается на неявно подразумеваемой, но неформулируемой аксиоме.
Помимо различного рода изъянов и недостатков в определениях и аксиомах «Начала» Евклида содержали также много неадекватных доказательств. Доказательства одних теорем были ошибочными; доказательства других охватывали лишь частный случай утверждения теоремы или конфигурации, о которой в ней говорилось. Такого рода недостатки не столь серьезны, так как их легче исправить. Евклид умышленно проводил правильные доказательства для фигур, весьма отдаленно напоминающих изображаемые. Но если судить о «Началах» в целом, то с полным основанием можно сказать, что в ряде случаев доказательства Евклида, касающиеся легко воспроизводимых на чертежах фигур, имели дефекты. Короче говоря, логика в «Началах» Евклида оставляла желать лучшего. Несмотря на все недостатки евклидовых «Начал», лучшие математики, естествоиспытатели и философы примерно до конца XVIII в. видели в них идеал математической строгости. Паскаль в своих «Мыслях» выразил это всеобщее восхищение так: «Геометрический дух во всем превосходит те предметы, которые поддаются законченному анализу. Он начинает с аксиом и выводит заключения, истинность которых может быть доказана с помощью универсальных логических правил». Учитель и предшественник Ньютона по кафедре в Кембриджском университете Исаак Барроу перечислил восемь причин непогрешимости геометрии: ясность геометрических понятий; однозначность определений; наша интуитивная уверенность в универсальной истинности общих геометрических понятий; правдоподобность и наглядность геометрических постулатов; малочисленность геометрических аксиом; ясное понимание способа получения всех величин; четкая последовательность доказательств; отказ от использования всего неизвестного. Такого рода признания достоинств геометрии можно было бы продолжить. В 1873 г. известный специалист по теории чисел Генри Джон Стивен Смит сказал: «Геометрия обратилась бы в ничто, если бы не ее строгость… Почти всеми признано, что методы Евклида безупречны с точки зрения строгости». Тем не менее, работая над созданием неевклидовой геометрии, математики обнаружили в евклидовой схеме построения геометрии столь большое число дефектов, что восхищаться ее совершенством было уже невозможно. Неевклидова геометрия стала тем рифом, о который разбилась геометрия Евклида. То, что ранее казалось надежной твердью, в действительности оказалось предательской топью. Разумеется, евклидова геометрия составляет лишь часть математики. С начала XVIII в. гораздо более обширной стала часть математики, посвященная свойствам чисел. Но как же развивалось логическое понятие числа? В Древнем Египте и Вавилоне уже были хорошо знакомы с целыми числами, дробями и даже с такими иррациональными числами, как √2 или √3. Для практических приложений иррациональные числа аппроксимировали рациональными. Но поскольку математика в Древнем Египте, Вавилоне и даже вплоть до IV в. до н.э. в Древней Греции строилась на интуитивной или эмпирической основе, как восхищение ее логической структурой, так и ее критика были в равной степени беспредметны. Первое известное нам логически последовательное изложение теории целых чисел содержится в VII, VIII и IX книгах «Начал» Евклида. В них Евклид предлагает, например, такие определения: «Единица есть [то], через что каждое из существующих считается единым; число же — множество, составленное из единиц» ([25], кн. VII-X, с. 9). Ясно, что подобные определения мало что говорят — в их формулировках отражается тот факт, что как в арифметике Евклида, так и в его геометрии проявляется непонимание необходимости неопределяемых понятий. При выводе свойств целых чисел Евклид использует уже упоминавшиеся общие понятия. К сожалению, некоторые из приведенных им доказательств ошибочны. Тем не менее древние греки и их преемники считали, что теория целых чисел обоснована вполне удовлетворительно. Более того, они, не церемонясь, позволяли себе говорить об отношениях целых чисел (у последующих поколений математиков такие отношения получили название дробей), хотя отношения целых чисел не были ими никак определены. В логическом развитии теории чисел древние греки столкнулись с трудностью, оказавшейся для них непреодолимой. Как известно, пифагорейцы в V в. до н.э. первыми подчеркнули важность целых чисел и отношений целых чисел для изучения природы. Более того, именно в целых числах и их отношениях пифагорейцы видели «меру» всего. Когда же обнаружилось, что некоторые отношения, например отношение гипотенузы равнобедренного прямоугольного треугольника к катету, непредставимы в виде отношения целых чисел, это и удивило, и обеспокоило пифагорейцов. Отношения, представимые в виде отношений целых чисел, пифагорейцы назвали соизмеримыми, а отношения, непредставимые в виде отношений целых чисел, получили название несоизмеримых. Так, иррациональное число √2 может служить примером несоизмеримого отношения. Открытие несоизмеримых соотношений легенда приписывает Гиппазию из Метапонта (V в. до н.э.). По преданию, в тот момент, когда Гиппазий пришел к этому открытию, пифагорейцы находились в открытом море — и они выбросили Гиппазия за борт, обвинив его в том, что он привнес в мироздание элемент, противоречивший пифагорейскому учению о сводимости всех явлений природы к целым числам или к их отношениям. Доказательство того, что число √2 несоизмеримо с 1, т.е. иррационально, было предложено пифагорейцами. По Аристотелю, они доказали иррациональность √2 методом от противного (reductio ad absurdum), иначе говоря, избрали косвенный метод доказательства. Пифагорейцы показали, что если гипотенуза равнобедренного прямоугольного треугольника была бы соизмерима с катетом, то одно и то же число должно было бы быть и четным, и нечетным, что невозможно. Доказательство проводилось следующим образом. Предположим, говорили пифагорейцы, что отношение гипотенузы к катету представимо в виде a/b, где a и b — взаимно-простые целые числа (т.е. предполагается, что общие множители, которые первоначально могли входить в числа a и b, уже сокращены). Если a/b = √2, то a2 = 2b2. Так как a2 — четное число, a также четно, поскольку квадрат любого нечетного числа нечетен.{62} Так как числитель и знаменатель отношения a/b не имеют общих делителей и a четно, число b должно быть нечетно. Число a как четное представимо в виде a = 2c, поэтому a2 = 4c2, а так как а2 = 2b2, то 4c2 = 2b2, или 2c2 = b2. Следовательно, b2 — четное число. Но тогда b также четное число, поскольку если бы оно было нечетным, то и квадрат его был бы нечетным. Но по доказанному ранее b — нечетное число; таким образом, мы приходим к противоречию. Пифагорейцы и древнегреческие мыслители классического периода, как правило, не принимали иррациональных чисел, ибо в их понимании иррациональные числа не были числами. Действительно, предложенное пифагорейцами доказательство говорит, что число √2 непредставимо в виде отношения целых чисел, но умалчивает о том, что такое иррациональное число. Жители Древнего Вавилона, как уже отмечалось, умели работать с иррациональными числами, но они, безусловно, не знали, что используемые ими десятичные (точнее, шестидесятеричные) приближения таких чисел не могут быть абсолютно точными. Мы можем восхищаться жизнелюбием древних вавилонян, но математиками они были неважными. Совсем иной склад ума был у древних греков: они не могли довольствоваться приближениями. Открытие иррациональных чисел поставило проблему, ставшую центральной для древнегреческой математики. Платон в своих «Законах» призывал к познанию несоизмеримых величин. Решение проблемы предложил Евдокс, некогда бывший учеником Платона: понятие величины надлежит трактовать геометрически. Длины, углы, площади и объемы, величины которых — если их выразить численно — могли оказаться иррациональными, следовало представлять геометрически. Именно так формулирует Евклид теорему Пифагора: квадрат, построенный на гипотенузе прямоугольного треугольника, равен сумме квадратов, построенных на обоих катетах. Под суммой квадратов Евклид понимает, что суммарная площадь фигуры, составленной из двух квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе. Обращение за помощью к геометрии здесь вполне понятно. Если числа 1 и √2 рассматривать как длины, т.е. как отрезки прямых, то принципиальное различие между 1 и √2 сглаживается и почти перестает быть заметным. Проблема, возникшая в связи с появлением иррациональных чисел, была шире, чем проблема численного представления длин, площадей и объемов, так как корни квадратных уравнений, например уравнения x2 − 2 = 0, вполне могли быть иррациональными числами. Греки классического периода решали такие уравнения геометрически, т.е. представляли их корни в виде отрезков, тем самым избегая необходимости обращаться к иррациональным числам. Так, если у вавилонян существовала формула для решения квадратного уравнения, то у греков сходную роль играло построение отрезка x, удовлетворяющего, скажем, уравнению х2 + ax = b2. Это направление в развитии математики получило название геометрической алгебры. Таким образом, «Начала» Евклида — трактат не только по геометрии, но и по алгебре. Превращение всей математики, за исключением разве лишь теории целых чисел, в геометрию привело к нескольким важным последствиям. Прежде всего оно усилило разрыв между теорией чисел и геометрией, ибо несоизмеримые величины целиком подлежали юрисдикции геометрии — арифметике (теории чисел) они были, так сказать, «неподсудны». Со времен Евклида между теорией чисел и геометрией приходилось проводить резкую границу.{63} А поскольку геометрия охватывала значительную часть математики, именно она и стала (по крайней мере до XVII в.) основой почти всей «строгой» математики. Мы до сих пор называем x2 «икс квадратом», x3 — «икс кубом», а не x соответственно во второй и в третьей степени, потому что некогда под x2 и x3 понимался лишь геометрический смысл этих величин. Разумеется, геометрическое представление чисел и операций над ними не очень подходило для практических целей. Логически вполне удовлетворительно представлять произведение √2′√3 как площадь прямоугольника. Но если требуется вычислить это произведение, то такого представления явно недостаточно. В естествознании и технике геометрические фигуры значительно менее полезны, чем численный ответ, полученный с требуемой точностью. В приложениях математики и в технике интерес представляют главным образом количественные результаты. Судоводителю в открытом море необходимо знать местоположение судна — численные значения его координат в градусах широты и долготы. Чтобы строить прочные и надежные здания, мосты, суда и плотины, также необходимо знать количественные меры длин, площадей и объемов деталей каждого сооружения. Более того, количественные характеристики, размеры, деталей сооружения необходимо знать заранее, до того как начнется постройка. Но греки классического периода, превыше всего ценившие строгие рассуждения и с пренебрежением относившиеся к приложениям математики в торговых расчетах, навигации, строительстве и составлении календарей, были удовлетворены полученным геометрическим решением проблемы иррациональных чисел. На смену греческой цивилизации эпохи высокой классики (афинский период) около III в. до н.э. пришла эпоха эллинизма (александрийский период), сложившаяся в результате слияния классической греческой культуры с культурами Египта и Вавилона (гл. I). С точки зрения логики математика александрийского периода представляла собой любопытное смешение дедуктивных и эмпирических подходов. Наиболее выдающиеся математики александрийской эпохи Архимед и Аполлоний следовали образцу аксиоматической, дедуктивной геометрии «Начал» Евклида. Даже в своих трудах по механике Архимед начинал с аксиом и доказывал теоремы, став предтечей Ньютона и его последователей, создавших «математическую физику». Но под влиянием более прагматичных египтян и вавилонян александрийцы начали использовать математику и для удовлетворения запросов практики. В Александрии были выведены формулы, позволяющие вычислять количественные меры длин, площадей и объемов. Так, Герон (I в.) в своем сочинении «Метрика» привел формулу для вычисления площади S треугольника.{64} 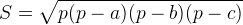 , ,где a, b, c — длины сторон треугольника, p — его полупериметр. Вычисление площади треугольника по формуле Герона нередко приводит к иррациональным числам. Формула Герона замечательна еще в одном отношении: в отличие от греков эпохи высокой классики, которые считали бессмысленным произведение более чем трех чисел, поскольку ему нельзя было придать геометрический смысл, Герон был чужд подобных предрассудков. Во многих чистых и прикладных науках, развитых греческими учеными александрийского периода — составление календаря, измерение времени, навигационные расчеты, оптика, география, пневматика и гидростатика (гл. I), — иррациональные числа находили самое широкое применение. Высшим достижением александрийцев стало создание Гиппархом и Птолемеем количественной астрономии — геоцентрической системы мира, позволившей человеку предсказывать движение планет, Солнца и Луны (гл. I). Для построения своей количественной теории Гиппарх и Птолемей разработали тригонометрию — область математики, занимающуюся вычислением одних элементов треугольника по данным о других его элементах. Так как подход Птолемея к построению тригонометрии отличался от принятого в то время, ему пришлось вычислять длины хорд окружности. Хотя для получения основных результатов об отношениях длин одних хорд к длинам других Птолемей использовал дедуктивно-геометрический метод, в процессе вычислений длин хорд (а именно они и были конечной целью расчетов) он широко применял арифметику и зачатки алгебры. Длины большинства хорд выражались иррациональными числами. Птолемей довольствовался получением рациональных приближений нужных ему величин, но в ходе вычислений, не колеблясь, употреблял и иррациональные числа. Арифметика и алгебра, столь свободно используемые александрийцами, которым они достались по наследству от египтян и вавилонян, были лишены логической основы. Птолемей и другие ученые александрийского периода, как правило, перенимали у древних египтян и вавилонян эмпирический подход к математике. Такие иррациональные числа, как π, √2, √3 и другие, вводились некритически и в случае необходимости заменялись рациональными приближениями. Наиболее известный пример использования иррациональных чисел — приближенное вычисление Архимедом числа π. По оценкам Архимеда, значение π заключено между 31/7 и 310/71. Независимо от того, знал или нет Архимед, что число π иррационально, найденные им приближенные значения π содержали нескончаемые нагромождения квадратных корней ([33], с. 266-270, 528-553), а извлечение квадратного корня чревато появлением иррациональных чисел, о чем не мог не знать Архимед. Для нашего повествования возрождение александрийскими математиками египетской и вавилонской алгебры, не зависящей от геометрии, имеет ничуть не меньшее значение, чем свободное использование иррациональных чисел. Выдающуюся роль в «оживлении» старой традиции сыграли Герон и еще один представитель александрийской школы — Диофант (примерно III в.). И Герон, и Диофант считали, что алгебраические и арифметические задачи представляют самостоятельный интерес и что обращение к геометрии излишне, поскольку не придает ни большей значимости задачам, ни большей логичности решениям. Герон формулировал и решал алгебраические задачи чисто арифметическими средствами. Например, дан квадрат, такой, что сумма его площади и периметра равна 896{65}; требуется найти сторону квадрата. Чтобы решить квадратное уравнение, к которому сводится задача, Герон добавляет к обеим частям полученного равенства по 4 и извлекает из них квадратный корень. Герон не доказывает правильности своих действий, а лишь указывает, в какой последовательности их надлежит выполнить. В работах Герона имеется немало задач такого рода. В своей «Геометрике» Герон говорит о сложении площади круга, длины окружности и диаметра. Разумеется, под этим он понимает сложение численных значений этих величин. Говоря об умножении квадрата на квадрат, Герон также имеет в виду вычисление произведения тех чисел, которыми выражаются площади квадратов. Тем самым Герон как бы осуществил перевод многого из того, что достигла геометрическая алгебра древних греков, на язык арифметических и алгебраических операций. Некоторые из задач, рассмотренных Героном и его ближайшими последователями, в точности совпадают с задачами, встречающимися в вавилонских и египетских текстах за 2000 лет до н.э. Следует подчеркнуть, что свои алгебраические работы греки излагали в описательной манере. Ни к какой символике они не прибегали. Не приводили они и доказательств правильности используемых приемов. Со времен Герона задачи, приводящие к уравнениям, стали довольно распространенным типом головоломок. В александрийский период алгебра достигла своего наивысшего расцвета в трудах Диофанта. О происхождении и жизни этого ученого почти ничего не известно. К сожалению, труды Диофанта, намного превосходившие по глубине и значимости сочинения его современников, появились слишком поздно, чтобы оказать сколько-нибудь заметное влияние на развитие математики того времени; разрушительная волна (гл. II) уже надвигалась, погребая под собой греческую цивилизацию. Несколько книг, написанных Диофантом, безвозвратно утеряно, однако шесть частей величайшего сочинения Диофанта «Арифметика», содержавшего, по утверждению самого автора, всего тринадцать частей, дошли до нашего времени [34]. Подобно египетскому папирусу Ринда, «Арифметика» Диофанта представляет собой сборник разрозненных задач. В посвящении говорится, что «Арифметика» задумана как серия задач, призванных помочь одному из учеников Диофанта овладеть различными видами чисел (Диофант [34], с. 41). Одной из значительных заслуг Диофанта является введение в алгебру некоторой символики. Поскольку мы располагаем не подлинными рукописями самого Диофанта, а лишь поздними (датируемыми не ранее чем XIII в.) копиями, трудно говорить с уверенностью, какими именно символами пользовался сам Диофант. Известно лишь, что он ввел символы, соответствующие нашим обозначениям x, степеням неизвестного x вплоть до x6 и 1/x. Появление такой символики замечательно само по себе, но еще больший интерес представляет введение степеней выше третьей, поскольку, как мы уже отмечали, греки классического периода игнорировали произведения более чем трех сомножителей, так как считали их не имеющими геометрического смысла. Но если подходить к умножению с чисто арифметических позиций, то произведения более трех сомножителей, разумеется, становятся вполне законными. Именно такой подход к произведениям трех и более чисел был избран Диофантом. Свои решения Диофант излагал словесно — так, как мы пишем прозу. Все необходимые действия он производил исключительно арифметически, не прибегая к геометрии для иллюстрации или в подтверждение своих рассуждений. Произведение (x − 1)(x − 2) Диофант вычислял чисто алгебраически, как это делаем мы. Использовал он и алгебраические тождества, например равенство a2 − b2 = (а − b)(a + b) и более сложные. Строго говоря, в своих вычислениях Диофант выполнял действия, основанные на использовании алгебраических тождеств, хотя сами тождества в явном виде у него не встречались. Алгебра Диофанта обладала еще одной особенностью: Диофант охотно решал неопределенные уравнения, например одно уравнение с двумя неизвестными. Такие уравнения математики рассматривали и до Диофанта. Так, пифагорейцы нашли целочисленные решения уравнения{66} x2 + y2 = z2. Аналогичные уравнения рассматривались и в других сочинениях. Но Диофант был первым, кто предпринял систематические и обширные исследования неопределенных уравнений, став тем самым основателем нового раздела алгебры, называемого ныне диофантовым анализом.{67} Хотя применение алгебры снискало Диофанту широкую известность, нельзя не отметить, что он признавал только положительные рациональные корни и отбрасывал все остальные. Даже при решении квадратного уравнения с одним неизвестным, имеющего два положительных рациональных корня, Диофант приводил только один (больший) корень. Если же уравнение имело два отрицательных корня, иррациональные или комплексные, то Диофант отвергал такое уравнение, считая его неразрешимым. Если уравнение, имело иррациональные корни, то Диофант шаг за шагом, от конца к началу, прослеживал полученное решение и показывал, как изменить исходное уравнение, чтобы новое уравнение имело рациональные корни. В этом Диофант отличался от Герона и Архимеда. Герон был инженером, и возникавшие в его расчетах иррациональные числа не пугали его. Для Герона иррациональные величины были вполне приемлемыми, хотя он, разумеется, и заменял их рациональными приближениями. Архимед также стремился получить точные решения и, если ответы выражались иррациональными числами, указывал границы, в которых те были заключены. Нам не известно доподлинно, как Диофант пришел к своим уравнениям (см. [34]). Поскольку Диофант не пользовался геометрией, маловероятно, что он лишь переложил методы Евклида, приспособив их к решению квадратных уравнений. К тому же у Евклида не встречаются неопределенные уравнения: Диофант был первым из математиков, занявшихся систематическим исследованием таких уравнений. Мы не знаем, существовала ли преемственность в науке в конце александрийского периода, и поэтому нам трудно установить, в какой мере сказались на работах Диофанта идеи его древнегреческих предшественников. Использованные Диофантом методы решения уравнений имеют гораздо больше общего с традициями вавилонской математики. Ее влияние на Диофанта косвенно подтверждается и другими фактами. Однако алгебра Диофанта существенно отличается от вавилонской: Диофант ввел символику и стал систематически решать неопределенные уравнения. В целом деятельность Диофанта стала заметной вехой в истории алгебры. Работы Герона и Диофанта, Архимеда и Птолемея по различным вопросам арифметики и алгебры не отличались по своему стилю от «рецептурных» текстов египтян и вавилонян, содержавших четкие указания относительно того, что и в какой последовательности следует делать. Дедуктивные, проводимые «по всей форме» доказательства геометрии Евклида, Аполлония и Архимеда были здесь преданы забвению. Все проблемы рассматривались индуктивно: автор указывал способ решения конкретной задачи, предположительно пригодный для решения более широкого круга задач, границы которого были нечетки. Нужно ли говорить, что при этом различные типы чисел (целые числа, дроби, иррациональные числа) вообще не определялись, если не считать маловразумительных определений целых чисел, предложенных Евклидом. Не существовало и аксиоматической основы, на которой можно было бы построить дедуктивную систему, пригодную для решения арифметических и алгебраических проблем. Таким образом, греки завещали потомкам две совершенно различные математические науки: с одной стороны — дедуктивную, систематически развитую и излагаемую, хотя и не свободную от ошибок, геометрию, с другой — эмпирическую арифметику и алгебру как ее обобщение. Поскольку, согласно представлениям греческих мыслителей классического периода, математические результаты должны были выводиться дедуктивно и базироваться на явно заданной аксиоматической основе, возникновение независимых арифметики и алгебры, не обладающих собственной логической структурой, привело к одной из величайших аномалий в истории математики. Индийцы и арабы, подхватившие эстафету развития математики после окончательного уничтожения арабами эллинистической (александрийской) греческой цивилизации, в еще большей мере нарушили концепцию математики, сложившуюся у греков классического периода. Подобно своим предшественникам — грекам, индийские и арабские математики использовали целые числа и дроби, но они, не колеблясь, оперировали и иррациональными числами. Именно они ввели новые, верные, правила сложения, вычитания, умножения и деления иррациональных чисел. Как же индийцам и арабам удалось придумать правила, лишенные логического обоснования и тем не менее оказавшиеся верными? Загадка решается довольно просто: индийцы и арабы рассуждали по аналогии. Так, правило √ab = √a′√b они считали верным для любых чисел a и b, поскольку оно выполнялось, например, в случае √36 = √4′√9. Фактически индийцы считали, не оговаривая этого специально, что с квадратными корнями из целых чисел можно обращаться так же, как с целыми числами. Индийцы были менее изощренными математиками, чем греки, и не видели, какие логические трудности таятся в понятии иррационального числа. Интересуясь «рецептурной», или алгоритмической, стороной вычислений, индийцы не заметили те различия, которым греки придавали столь большое значение. Но производя сложение и вычитание, умножение и деление иррациональных чисел по таким же правилам, по каким производятся арифметические операции над рациональными числами, индийцы внесли посильный вклад в развитие математики. Кроме того, вся их арифметика была полностью независимой от геометрии. Введя в обращение отрицательные числа для обозначения денежных долгов, или пассива, индийцы преумножили и без того многочисленные логические трудности математиков (положительные числа при таком подходе должны означать наличность, или актив). Первым ввел отрицательные числа Брахмагупта (около 628 г.), но он лишь сформулировал правила четырех арифметических действий над отрицательными числами, не приведя никаких определений, аксиом или теорем. Выдающийся индийский математик XII в. Бхаскара обратил внимание на то, что квадратный корень из положительного числа имеет два значения — положительное и отрицательное. Бхаскара рассмотрел также вопрос о квадратном корне из отрицательных чисел и пришел к выводу, что такой корень не существует, так как иначе его квадрат должен был бы быть отрицательным числом, а отрицательное число не может быть квадратом. Далеко не все индийцы восприняли нововведение Бхаскары. Даже сам Бхаскара, приводя в качестве решений одной задачи два числа (50 и −50), утверждал: «Второе значение следует отбросить как неприемлемое, ибо люди не одобряют отрицательных решений». Тем не менее отрицательные числа вскоре после того, как они были введены, начали распространяться все шире. Индийцам удалось достичь некоторых успехов и в алгебре. Для описания операций и неизвестных они ввели сокращенные слова и специальные символы, И хотя символика индийцев не была всеобъемлющей, их алгебра обладала определенными преимуществами по сравнению с алгеброй Диофанта. Решая задачу, индийцы указывали только основные этапы решения, не приводя никаких обоснований или доказательств. Отрицательные и иррациональные корни квадратных уравнений индийцы рассматривали наряду с положительными и рациональными корнями. В действительности индийцы обращались с алгеброй еще более свободно, чем мы здесь говорили. Например, из тригонометрии известно, что sin2α + cos2α = 1 при любом угле α. Для Птолемея, одного из создателей тригонометрии и автора ее первого систематического изложения, это соотношение было геометрическим утверждением о соотношении между длинами хорд в окружности. Хотя, как мы отмечали, Птолемей свободно пользовался арифметикой, выражая неизвестные длины через известные, он в основном опирался на геометрию и приводимые им аргументы были геометрическими. Индийцы же оперировали с тригонометрическими отношениями, по существу, так, как мы сейчас, — для них это были просто числа. Вычисляя cos α по известному sin α, они свободно использовали соотношение sin2α + cos2α = 1, применяя затем простейшие преобразования своих формул. Таким образом, при выводе и записи соотношений между синусами и косинусами углов индийская тригонометрия полагалась не столько на геометрию, сколько на алгебру. Мы видим, что арифметика и вычислительные возможности математики интересовали индийцев несравненно больше, чем дедуктивные схемы рассуждений, и что основной вклад они внесли именно в развитие арифметики и разработку практических приемов вычислений. Математику индийцы называли ганита, что означает «наука о вычислениях». Они предложили немало удобных методов вычислений и усовершенствовали известные ранее приемы счета, но, судя по всему, совсем не рассматривали доказательств. Индийцы пользовались определенными математическими правилами, не задумываясь над логической обоснованностью своих действий. Ни одну область математики индийцы не обогатили ни общими методами, ни радикально новыми идеями. Можно с уверенностью сказать, что индийцы не сознавали значимости собственного вклада в развитие математики. Те немногие удачные идеи, которые они внесли в математику (введение особых символов для обозначения чисел от 1 до 9; переход от позиционной системы записи чисел с основанием 60 к десятеричной системе; введение отрицательных чисел и признание нуля полноправным числом), возникали случайно, и, судя по всему, индийские математики не понимали истинной значимости таких нововведений. Индийцы с полным безразличием относились к математической строгости. Выдвигаемые ими тонкие идеи они с поразительным равнодушием смешивали с грубыми соображениями египтян и вавилонян. Среднеазиатский ученый-энциклопедист аль-Бируни (973 — около 1050) писал об индийцах: Я могу сравнить то, что содержится в их книгах по арифметике и другим математическим наукам, только с перламутром, смешанным с незрелыми финиками, или с жемчужинами вперемешку с навозом, или с кристаллами, перемешанными с камешками. Обе части имеют для них равную ценность, поскольку у них нет примера восхождения к вершинам логического познания. ([35], с. 69.) Так как индийцы питали особую склонность к арифметике и внесли основной вклад в развитие арифметики и алгебры, их деятельность привела к расширению той части математики, которая опиралась на эмпирическую и интуитивную основу. В то время как индийцы практически игнорировали дедуктивную геометрию, арабы предприняли критическое изучение геометрических работ древних греков и по достоинству оценили роль дедуктивного доказательства в становлении геометрии. Однако в отношении к арифметике и алгебре, которым в арабской математической литературе отводилась более значительная роль, чем геометрии, арабы фактически мало чем отличались от индийцев. Арабов, как и их индийских предшественников, устраивало рассмотрение арифметики и алгебры на эмпирической, конкретной и интуитивной основе. Правда, некоторые арабские математики приводили геометрические соображения в обоснование решения квадратных уравнений, но в целом подход к решению и методология у арабов в отличие от греков классического периода по существу были алгебраическими. Кубические уравнения, например уравнение x3 + 3x2 + 7x − 5 = 0, арабы решали, используя только геометрические построения, так как алгебраический метод решения таких уравнений еще не был открыт. Но их геометрические построения было бы невозможно выполнить с помощью циркуля и линейки, а доводы, приводимые в обоснование построений, не имели строго дедуктивного характера. На протяжении всех столетий, пока арабы активно занимались математикой, в своих оригинальных работах они мужественно сопротивлялись соблазнам точного рассуждения. Наиболее интересной особенностью математики индийцев и арабов является их внутренне противоречивое представление о предмете математического исследования. То, что египтяне и вавилоняне были склонны воспринимать немногие известные им арифметические и геометрические правила на эмпирической основе, само по себе не удивительно. Эмпирическая основа естественна почти для всех видов человеческого знания. Но индийцам и арабам было известно совершенно новое понятие математического доказательства, доставшееся им в наследство от греков. Однако они не позаботились о том, чтобы применить понятие дедуктивного доказательства в арифметике и алгебре. Отношение индийцев к математике можно в какой-то степени объяснить. Индийцы не придавали особого значения тем немногим достижениям греческой математики классического периода, которые были им известны, и следовали в основном александрийскому подходу к арифметике и алгебре. Но арабы были хорошо осведомлены о греческой геометрии и даже, как упоминалось, предприняли попытку критического пересмотра результатов своих предшественников. Кроме того, на протяжении нескольких веков и арабы, и индийцы находились в благоприятных для занятий чистой наукой условиях — и ничто не вынуждало математиков жертвовать доказательством ради немедленной практической отдачи. Как могло случиться, что два эти народа подошли к развитию двух областей математики совершенно иначе, чем греки классического периода и многие из александрийцев? На этот вопрос существует несколько возможных ответов. Прежде всего, индийские и арабские математики, несмотря на арабские комментарии к дедуктивной геометрии, по существу некритически отнеслись к греческому наследию. Возможно, именно поэтому они восприняли математику такой, какой она пришла к ним: геометрия, по их мнению, должна была оставаться дедуктивной, арифметика и алгебра — эмпирическими и эвристическими. Возможно и другое объяснение: и индийцы, и арабы, в особенности последние, по достоинству оценили высокие стандарты строгости в геометрии, столь разительно отличающиеся от требований, предъявляемых к арифметике и алгебре, но не сумели подвести под арифметику надлежащий логический фундамент. В пользу такого предположения говорит хотя бы то, что арабы приводили в подтверждение решений квадратных и кубических уравнений некоторые геометрические соображения. Не исключены и другие объяснения. Так, индийцы и арабы отдавали предпочтение арифметике, алгебре и алгебраической формулировке тригонометрических соотношений. Подобное предрасположение может свидетельствовать об ином складе ума, оно может быть обусловлено и какими-то особенностями индийской и арабской культур. Обе эти цивилизации превыше всего ставили запросы практики, а для удовлетворения практических потребностей — как мы уже отмечали, говоря о развитии математики в александрийский период, — были необходимы количественные результаты, которые давали именно арифметика и алгебра. В пользу предположения о различных складах ума косвенно свидетельствует и реакция европейцев на математическое наследие, доставшееся им от индийцев и арабов. Как мы увидим в дальнейшем, европейцы были гораздо сильнее, чем арабы и индийцы, обеспокоены логическими проблемами в построении арифметики и геометрии. Безрассудная смелость индийцев и арабов вывела на передний план арифметику и алгебру (если говорить о практической полезности), поставив их почти наравне с геометрией (см., например, [9], [36], [37]). Когда в конце средневековья и в период Возрождения европейцы — отчасти через арабов, отчасти непосредственно из сохранившихся греческих рукописей — ознакомились с существующим уровнем достижений математики, они своеобразно разрешили дилемму, возникшую в связи с разделением математики на два типа «знания». Настоящей математикой, по мнению европейцев, заведомо была только дедуктивная геометрия греков. Но в то же время они не могли и не хотели отрицать полезность и эффективность арифметики и алгебры, которые хотя и были лишены твердого логического фундамента, но уже значительно усовершенствовались по сравнению с классической древностью. Первая проблема, с которой столкнулись европейцы, сводилась к старому вопросу о том, как следует относиться к иррациональным числам. Итальянский математик Лука Пачоли (ок. 1445-1514), немецкий монах и профессор математики в Йене Михаэль Штифель (1486(?)-1567), итальянский врач и ученый Джироламо Кардано (1501-1570) и фламандский военный инженер Симон Стевин (1548-1620) свободно использовали иррациональные числа, следуя здесь традиции индийцев и арабов, и ввели много новых типов иррациональностей. Так, Штифель оперировал с иррациональными выражениями вида 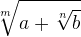 , ,а Джироламо Кардано — с иррациональностями, содержащими кубические корни. Примером того, насколько свободно и широко европейцы использовали иррациональности, может служить выражение для числа π, полученное Франсуа Виетом (1540-1603). Рассматривая правильные многоугольники с 4, 8, 16 и более сторонами, вписанные в окружность единичного радиуса, Виет обнаружил, что 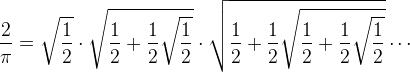 . .Иррациональные числа нашли широкое применение и в связи с одним из новых достижений математики эпохи Возрождения — логарифмами. Логарифмы положительных чисел были изобретены в конце XVI в. Джоном Непером{68} (1550-1617) для той самой цели, для которой они с тех пор и употребляются, — для ускорения арифметических вычислений. И хотя логарифмы большинства положительных чисел иррациональны (а предложенный Непером метод вычисления логарифмов основан на свободном обращении с иррациональными числами), все математики приветствовали полезное изобретение, избавившее их от излишнего труда. Вычисления с иррациональностями производились без каких-либо затруднений, но кое-кого все же беспокоила проблема, можно ли считать иррациональные числа «настоящими». Так, Штифель в своем главном труде «Полная арифметика» (Arithmetica integra, 1544), посвященном арифметике и алгебре, вторя Евклиду, высказывал предположение, что величины (геометрическая теория Евклида) отличны от чисел; однако, следуя духу достижений своего времени, он выражал иррациональные числа в десятичной системе. Штифеля беспокоило, что для записи иррационального вдела в десятичной системе требуется бесконечно много знаков. С одной стороны, рассуждал он, так как при доказательстве [свойств] геометрических фигур иррациональные числа заменяют рациональные всякий раз, когда те отказываются служить нам, и доказывают все то, что не могли бы доказать те… приходится признать, что они [иррациональные числа] являются истинными числами. К тому же нас вынуждают и результаты, проистекающие из их применения, которые нельзя не признать подлинными, достоверными и незыблемыми. С другой стороны, иные соображения заставляют нас отрицать, что иррациональные числа вообще являются числами. Такое сомнение подкрепляется тем, что если мы попытаемся записать иррациональные числа в десятичной форме… то обнаружим, что они непрестанно ускользают от нас и ни одно из них не удается постичь точно… Число же, которому в силу его природы недостает точности, не может быть названо истинным числом… Следовательно, подобно тому как не является числом бесконечность, иррациональное число также не является истинным числом, а как бы скрыто от нас в облаке бесконечности. Далее Штифель добавляет, что настоящие числа — это либо целые числа, либо дроби, а поскольку иррациональные числа не принадлежат ни к тем, ни к другим, их нельзя считать настоящими числами. Столетие спустя Паскаль и Барроу утверждали, что иррациональные числа не более чем символы, не существующие независимо от геометрических величин, и что логика арифметических операций, производимых над иррациональными числами, должна быть обоснована с помощью теории величин Евклида, хоть эта теория и не в полной мере отвечала поставленной так задаче.{69} Высказывались и иные утверждения: по мнению некоторых европейских математиков, иррациональные числа с полным основанием можно было считать настоящими числами. Стевин провозгласил иррациональности числами и построил ряд все более точных приближений их с помощью рациональных чисел. Джон Валлис (1616-1703) в своей «Алгебре» (1685) также признал, что иррациональные числа являются числами в полном смысле этого слова. Однако ни Стевин, ни Валлис не привели никаких логических аргументов в подтверждение своего мнения. Более того, когда Декарт в своей «Геометрии» (1637) и Ферма в рукописи 1629 г. разработали аналитическую геометрию, ни тот, ни другой не имели ясного представления об иррациональных числах. Тем не менее оба исходили из предположения, что между всеми положительными действительными числами и точками на прямой существует взаимно-однозначное соответствие, т.е. что расстояние от любой точки на прямой до какой-то точки, принятой за начало отсчета, может быть выражено числом. Так как многие из чисел при этом оказывались бы иррациональными, Декарт и Ферма тем самым неявно допускали существование иррациональных чисел, несмотря на то что тогда оно еще никак не было логически обосновано. Европейцам пришлось столкнуться и с проблемой отрицательных чисел. Эти числа стали известны в Европе из арабских текстов, но большинство математиков XVI-XVII вв. не считали отрицательные числа «настоящими» или утверждали, что отрицательные числа не могут быть корнями уравнений. Никола Шюке [1445(?)-1500(?)] в XV в. и Штифель в XVI в. заявляли, что отрицательные числа лишены всякого смысла. Кардано включал отрицательные величины в число корней рассматриваемых им уравнений, но полагал, что отрицательные корни — это просто символы, не имеющие реального смысла. Отрицательные корни уравнений Кардано называл фиктивными и противопоставлял их действительным, т.е. положительным, корням. Виет полностью отвергал отрицательные числа. Декарт принимал их лишь с определенными оговорками. Отрицательные корни уравнений Декарт называл ложными на том основании, что они якобы представляют числа, которые меньше, чем ничто. Однако Декарту удалось показать, как, исходя из любого уравнения, можно построить другое уравнение, корни которого больше корней исходного на любую заданную величину. Тем самым Декарт указал способ, позволяющий преобразовать уравнение с отрицательными корнями в уравнение с положительными корнями. «Фиктивные» корни при таком преобразовании переходили в действительные, и поэтому Декарт неохотно смирился с отрицательными числами, но сомнения и тревоги так и не оставили его.{70} Паскаль считал, например, вычитание числа 4 из 0 операцией, лишенной всякого смысла. В «Мыслях» Паскаля есть выразительное признание: «Я знаю людей, которые никак не могут понять, что если из нуля вычесть четыре, то получится нуль». Интересный довод против отрицательных чисел выдвинул близкий друг Паскаля теолог и математик Антуан Арно (1612-1697). Арно усомнился в том, что −1:1 = 1:−1. Как может выполняться такое равенство, спрашивал он, если −1 меньше, чем 1? Ведь меньшее число не может относиться к большему так же, как большее к меньшему. Лейбниц, признав правильность возражения Арно, указал, что такого рода пропорции вполне допустимо использовать в вычислениях, ибо по форме они правильны, и сравнил действия, производимые над отрицательными числами, с действиями, производимыми над мнимыми величинами, введенными незадолго до этого. Тем не менее Лейбниц затемнил существо дела, предложив называть мнимыми (несуществующими) все величины, не имеющие логарифма. По мнению Лейбница, число −1 не существует, так как положительные логарифмы соответствуют числам, большим 1, а отрицательные логарифмы (!) соответствуют числам, заключенным между 0 и 1. Следовательно, для отрицательных чисел логарифмов просто «не хватает». Действительно, если бы нашлось какое-нибудь число, соответствующее log(−1), то половина его, как следует из теории логарифмов, соответствовала бы log√−1, a √−1 заведомо не имеет логарифма. Одним из первых алгебраистов, умышленно не переносившим отрицательный коэффициент в другую часть уравнения, был Томас Гарриот (1560-1621). Однако он отвергал отрицательные корни и даже «доказал» в своем сочинении «Практические аналитические искусства» (Artis analyticae praxis, 1631), опубликованном уже после его смерти, что отрицательные корни не существуют. Ясные и четкие определения отрицательных чисел дал Рафаэль Бомбелли (XVI в.), хотя ему и не удалось обосновать правила действий над отрицательными числами, поскольку в то время отсутствовала логическая основа, необходимая для обоснования положительных чисел.{71} Стевин рассматривал уравнения с положительными и отрицательными коэффициентами и считал отрицательные корни вполне допустимыми. В своем сочинении «Новое изобретение в алгебре» (Invention nouvelle en algèbre, 1629) Альбер Жирар (1595-1632) не проводил никакого различия между отрицательными и положительными числами и указывал оба корня квадратного уравнения, даже если они были отрицательными. И Жирар, и Гарриот употребляли один и тот же знак «минус» для обозначения как операции вычитания, так и отрицательных чисел, хотя следовало бы ввести два отдельных символа, поскольку отрицательное число — независимое понятие, в то время как вычитание — одна из четырех арифметических операций. В целом можно сказать, что немногие математики XVI-XVII вв. свободно обращались с отрицательными числами или легко восприняли их введение, большинство заведомо не признавали отрицательные числа «настоящими» корнями алгебраических уравнений. По поводу отрицательных чисел среди математиков бытовали самые нелепые предрассудки. Так, Валлис, придерживавшийся прогрессивных для своего времени взглядов и не отвергавший отрицательных чисел, был убежден в том, что отрицательные числа больше, чем бесконечность, и в то же время меньше нуля. В своей «Арифметике бесконечно малых» (Arithmetica infinitorum, 1655) Валлис доказывал, что поскольку отношение a/0 при положительном a обращается в бесконечность, то, когда знаменатель становится отрицательным (отношение a/b с отрицательным b), отношение должно стать больше, чем a/0, так как отрицательный знаменатель меньше нуля. Следовательно, заключал Валлис, отрицательные числа должны быть больше, чем бесконечность. Некоторые из наиболее передовых мыслителей того времени — Бомбелли и Стевин — предложили представление чисел, которое, несомненно, способствовало принятию всей системы вещественных чисел. Бомбелли предположил, что существует взаимно-однозначное соответствие между вещественными числами и длинами отрезков, отложенными на прямой (с заданной единицей длины), и ввел для длин четыре основных действия. По мнению Бомбелли, вещественные числа и производимые над ними арифметические действия определяются длинами отрезков и соответствующими геометрическими операциями. Тем самым Бомбелли рационализировал систему вещественных чисел на геометрической основе. Стевин также рассматривал вещественные числа как длины и считал, что при подобной интерпретации исчезают все трудности, связанные с введением иррациональных чисел. Разумеется, при таком подходе вещественные числа оказались тесно связанными с геометрией. Так и не преодолев трудностей, связанных с иррациональными и отрицательными числами, европейцы еще более увеличили свое, и без того тяжкое, бремя, когда набрели на новое открытие, значение которого они осознали далеко не сразу, — комплексные числа. Новые числа возникли, когда математики распространили операцию извлечения квадратного корня на любые числа, которые только могут встретиться, например при решении квадратных уравнений. Так, Кардано в гл. 37 своего трактата «Великое искусство» (Ars magna, 1545) поставил и решил следующую задачу: разделить число 10 на две части, произведение которых равно 40. Эта на первый взгляд нелепая задача допускает решение, поскольку, как заметил Д'Аламбер, «алгебра щедра: она нередко дает больше, чем от нее можно было бы требовать». Если x — одна из частей, то по условиям задачи x(10 − x) = 40 и мы получаем для x квадратное уравнение. Решив его, Кардано нашел корни 5 + √−15 и 5 − √−15, относительно которых заметил, что эти «сложнейшие величины бесполезны, хотя и весьма хитроумны». «Умолчим о нравственных муках» и умножим 5 + √−15 на 5 − √−15. Произведение этих двух чисел равно 25 − (−15) = 40. По этому поводу Кардано философски заметил: «Арифметические соображения становятся все более неуловимыми, достигая предела столь же утонченного, сколь и бесполезного». Еще раз Кардано столкнулся с комплексными числами в связи с алгебраическим методом решения кубических уравнений, который он изложил в своей книге. Хотя Кардано искал и отбирал только вещественные корни, выведенная им формула давала и комплексные корни (если уравнение допускало комплексные корни). Небезынтересно отметить, что в том случае, когда все три корня уравнения были вещественными, формула Кардано приводила к комплексным числам, по которым можно было найти вещественные корни.{72} Таким образом, Кардано мог не придавать большого значения комплексным числам, но, поскольку он не знал, как извлекать из комплексных чисел кубический корень и, следовательно, как получать вещественные корни, ему так и не удалось преодолеть эту трудность. Вещественные корни Кардано находил другим способом. Бомбелли также рассматривал комплексные числа как решения кубического уравнения и сформулировал (практически в современном виде) правила выполнения четырех арифметических операций над комплексными числами, однако считал их бесполезной и хитроумной «выдумкой». Альбер Жирар признавал комплексные числа, по крайней мере как формальные решения уравнений. В частности, в работе «Новое изобретение в алгебре» Жирара говорится следующее: «Можно было бы спросить, для чего нужны эти невозможные решения [комплексные корни]. Я отвечу — по трем причинам: для незыблемости общих правил; чтобы не было других решений и по причине их полезности». Однако передовые взгляды Жирара не оказали сколько-нибудь заметного влияния на его коллег. Декарт также был среди тех, кто отвергал комплексные корни. Именно он ввел в употребление термин «мнимое число». В своей «Геометрии» Декарт утверждал: «Ни истинные, ни ложные [отрицательные] корни не бывают всегда вещественными, иногда они становятся мнимыми». Декарт считал, что отрицательные корни можно сделать «действительными», преобразуя исходное уравнение в уравнение с положительными корнями, тогда как комплексные корни превратить в вещественные невозможно. Следовательно, комплексные корни с полным основанием можно считать не настоящими, а мнимыми. Даже Ньютон не придавал особого значения комплексным корням, вероятнее всего потому, что в его время комплексные корни еще не имели физического смысла. Так, во «Всеобщей арифметике» ([139], изд. 2-е, 1728) Ньютон говорит: «Корни уравнений часто должны быть невозможными [комплексными] именно потому, что они призваны выражать невозможные случаи задачи так, как если бы те были возможны». Иначе говоря, задачи, которые не допускают решений, имеющих физический или геометрический смысл, должны иметь комплексные корни. Отсутствие ясности в вопросах, связанных с комплексными числами, часто демонстрируют на примере широкоизвестного высказывания Лейбница: «Дух божий нашел тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Хотя Лейбниц формально производил операции над комплексными числами, он не понимал их истинной природы. Желая хоть как-то обосновать те применения, которые он сам и Иоганн Бернулли нашли комплексным числам в математическом анализе, Лейбниц высказал надежду, что вреда от этого не будет. Несмотря на отсутствие ясного понимания природы комплексных чисел в XVI-XVII вв., алгоритмическая сторона вычислений, производимых с вещественными и комплексными числами, усовершенствовалась и расширялась. В своей «Алгебре» (1685) Валлис показал, как геометрически представить комплексные корни квадратного уравнения с вещественными коэффициентами. По существу, Валлис утверждал, что комплексные числа ничуть не более бессмысленны, чем отрицательные числа, а так как последние можно изобразить точками направленной прямой, то комплексные числа можно представить точками плоскости. Валлис предложил несовершенное представление комплексных чисел и способ, позволяющий геометрически построить корни уравнения ax2 + bx + c = 0 для случая вещественных и комплексных корней. Хотя работа Валлиса оказалась правильной, ее предали забвению, поскольку в то время, математики еще не могли по достоинству оценить применение комплексных чисел. Хотя в XVII в. в логике математики возникли и другие проблемы, мы рассмотрим их в следующей главе, а пока нас будут интересовать те трудности, с которыми столкнулись в XVIII в. математики, пытаясь осмыслить и обосновать все то, что они делали с иррациональными, отрицательными и комплексными числами, а также разобраться в алгебре. Что касается (положительных) иррациональных чисел, то, хотя они по-прежнему не были строго определены и их свойства по существу оставались неустановленными, все же чисто интуитивно такие числа были более приемлемы, поскольку по своим свойствам они в общем были близки к целым и дробным числам. Именно поэтому математики безбоязненно использовали их, не задумываясь ни о том, что собственно они означают, ни об их свойствах. Некоторые математики, в том числе и Эйлер, полагали, что логической основой теории иррациональных чисел служит теория величин Евдокса, изложенная в книге V «Начал» Евклида. Евдокс действительно создал теорию пропорций для величин, связанную с геометрией, но отнюдь не теорию иррациональных чисел.{69} Однако, что касалось иррациональных чисел, то здесь если не логика, то по крайней мере совесть ученых мужей XVII в. была чиста. Отрицательные числа беспокоили математиков гораздо сильнее, чем иррациональные; возможно, это объяснялось тем, что отрицательные числа не имели столь очевидного геометрического смысла и правила операций над ними выглядели менее привычно. Хотя примерно с середины XVII в. отрицательные числа использовались весьма широко, они были лишены строгого определения и логического обоснования, и многие математики либо пытались каким-то образом восполнить этот пробел, либо оспаривали само применение отрицательных чисел. В статье «Отрицательное», написанной для знаменитой французской «Энциклопедии», один из величайших мыслителей Века разума Жан Лерон Д'Аламбер утверждал: «Если задача приводит к отрицательному решению, то это означает, что какая-то часть исходных предположений ложна, хотя мы и считали ее истинной», — и далее: «Если получено отрицательное решение, то это означает, что искомым решением служит дополнение к [соответствующему положительному] числу».{73} Работа величайшего из математиков XVIII в. Леонарда Эйлера «Полное введение в алгебру» (1770) по праву принадлежит к числу самых значительных трудов по алгебре. В этой работе Эйлер обосновал эквивалентность операций вычитания величины −b и прибавления величины b, сославшись на то, что «погасить долг означает поднести дар». Равенство (−1)′(−1) = +1 Эйлер доказал следующим образом. Произведение (−1)′(−1), рассуждал он, может быть равно либо −1, либо +1, а поскольку ему удалось доказать, что 1′(−1) = −1, то для произведения (−1)′(−1) остается единственное возможное значение, а именно +1. В XVIII в. авторы даже наиболее выдающихся работ по алгебре не различали знак «минус» как символ операции вычитания и знак «минус» как символ отрицательного числа (например, −2). На протяжении XVIII в. против отрицательных чисел выдвигалось немало возражений. Английский математик, член совета Кларе-колледжа в Кембридже и член Королевского общества, Фрэнсис Мазер (1731-1824) был автором солидных работ по математике и фундаментального трактата по страхованию жизни. В 1759 г. он опубликовал «Рассуждение о применении в алгебре знака минус». Мазер показал, как избежать отрицательных чисел (исключение составляли лишь числа, получаемые в том случае, когда из меньшего числа необходимо вычесть большее), и в частности отрицательных корней уравнения. Он произвел тщательную классификацию квадратных уравнений: уравнения с отрицательными корнями Мазер рассматривал отдельно, а сами отрицательные корни рекомендовал отбрасывать. Аналогичным образом он поступал и с кубическими уравнениями. Об отрицательных корнях Мазер говорил: … Насколько я могу судить, они служат лишь для того, чтобы внести замешательство во всю теорию уравнений и сделать смутным и загадочным то, что по самой своей природе особенно ясно и просто… Чрезвычайно желательно поэтому не допускать отрицательные корни в алгебру, а если таковые все же возникнут, неукоснительно изгонять их. Имеются веские основания полагать, что если бы нам удалось избавиться от отрицательных корней, то тем самым были бы сняты возражения, выдвигаемые многими учеными и остроумными мужами против алгебраических вычислений как слишком сложных и наделенных почти непостижимыми для разума понятиями. Алгебра, или всеобщая арифметика, по самой своей природе, несомненно, является наукой не менее простой, ясной и пригодной для доказательства, чем геометрия. Еще более ожесточенными были споры о смысле комплексных чисел и применении этих чисел. И без того трудное положение осложнилось здесь тем, что некоторые математики стали рассматривать логарифмы отрицательных чисел (а также комплексных чисел), которые также должны были являться комплексными числами. С 1712 г. развернулась острая дискуссия о смысле комплексных чисел, и в частности о логарифмах отрицательных и комплексных чисел, в которой участвовали своими статьями и письмами Лейбниц, Эйлер и Иоганн Бернулли. Лейбниц и Бернулли воспользовались для обозначения комплексных чисел термином «мнимые», предложенным Декартом, понимая под мнимыми величинами (к ним они относили и отрицательные числа) числа, которые не существуют. Тем не менее и Лейбниц, и Бернулли, словно по волшебству, с немалой пользой применяли «несуществующие» числа в анализе, получая с их помощью, например, совершенно правильные формулы интегрирования: промежуточные выкладки, казалось бы, не имели смысла, но окончательный результат был верен. Лейбниц заявлял, что логарифмы отрицательных чисел не существуют, и в доказательство приводил различные аргументы. Иоганн Бернулли считал, что log a = log(−a), и в подтверждение также ссылался на различные доводы. Одно из «доказательств» опиралось на хорошо известные свойства логарифмов положительных чисел: log(−a) = 1/2′log(−a)2 = 1/2′log a2 = log a.
Другой аргумент, взятый Бернулли из математического анализа, приводил к тому же выводу. Переписка между Лейбницем и Иоганном Бернулли о логарифмах отрицательных чисел была весьма обширной, но — увы! — большинство утверждений, на которых настаивали обе стороны, были неверными. К правильному решению проблемы пришел Эйлер. Свой результат он изложил в работе «Исследования о мнимых корнях уравнений» (1751). Окончательный ответ, правильный по существу, но полученный с помощью неправильных рассуждений, применим ко всем комплексным числам, в том числе и к вещественным числам (если y = 0, то комплексное число x + iy обращается в вещественное число x); он имеет следующий вид: log(x + iy) = log(ρeiφ) = log ρ + i(φ + 2nπ){74},
где n — произвольное целое число. Однако современники Эйлера не поняли и не оценили эту его замечательную работу. О своих результатах Эйлер сообщил в письме Д'Аламберу от 15 апреля 1747 г., где обратил внимание на то, что даже у любого положительного вещественного числа существует бесконечно много логарифмов. Лишь один из них является вещественным числом, и именно его мы обычно используем в своих вычислениях с вещественными числами. Ни обширная переписка, ни работа Эйлера не убедили Д'Аламбера, и в своей заметке «О логарифмах отрицательных величин» он выдвинул всевозможные метафизические, аналитические и геометрические аргументы против существования таких логарифмов. Д'Аламбер преуспел в своем намерении: ему удалось основательно запутать и без того сложную проблему. Свои расхождения с Эйлером Д'Аламбер пытался скрыть, утверждая, будто речь идет лишь о различиях в формулировках, а не о принципиальных разногласиях по существу вопроса. Все участники острой полемики, развернувшейся вокруг проблемы расширения понятия числа, мыслили непоследовательно. В первой половине XVIII в. было принято считать, что некоторые операции над комплексными числами, например операция возведения комплексного числа в комплексную степень, могут привести к числам совершенно новой природы. Подобным представлениям положил конец Д'Аламбер, доказавший в своей работе «Размышления об общей причине ветров» (1747), что все операции, производимые над комплексными числами, порождают только комплексные числа. Доказательство Д'Аламбера было усовершенствовано Эйлером и Лагранжем, но решающий шаг здесь сделал именно Д'Аламбер. По-видимому, Д'Аламбер сознавал непоследовательность и даже противоречивость собственных представлений о комплексных числах. Во всяком случае, в «Энциклопедии», для которой он написал много математических статей, о комплексных числах ни разу не упоминается.{73} Не было полной ясности в вопросах, связанных с комплексными числами, и у Эйлера. В своей «Алгебре» (1770), лучшем учебном курсе XVIII в. по этой дисциплине, Эйлер утверждал: Квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Отсюда ясно, что квадратные корни из отрицательных чисел не могут находиться среди возможных [действительных, вещественных] чисел. Следовательно, нам не остается ничего другого, как признать их невозможными числами. Это приводит нас к понятию чисел, по своей природе невозможных и обычно называемых мнимыми или воображаемыми, потому что они существуют только в воображении. Производя операции над комплексными числами, Эйлер порой и ошибался. Так, в его «Алгебре» фигурирует равенство √−1′√−4 = √4 = 2, выписанное по аналогии с тождеством √a′√b=√ab, справедливым для положительных a и b, т.е. для вещественных корней. Называя комплексные числа невозможными, Эйлер в то же время отмечал их полезность. В частности, он считал комплексные числа полезными по той причине, что они якобы позволяют отличать задачи, имеющие решения, от задач, не имеющих решения. Так, если бы нам понадобилось разложить число 12 на две части, произведение которых должно было бы равняться 40 (намек на задачу Кардано), то мы обнаружили бы, что эти части равны соответственно 6 + √−4 и 6 − √−4, т.е., согласно Эйлеру, узнали бы, что задача неразрешима. Несмотря на множество принципиальных возражений против комплексных чисел, на протяжении XVIII в. их широко использовали, свободно применяя к ним правила арифметических действий над вещественными числами. Так математики получали практические навыки в обращении с комплексными числами. В тех случаях, когда комплексные числа применялись лишь на промежуточных стадиях математических доказательств, полученные с их помощью окончательные результаты всегда оказывались верными, что не могло не произвести благоприятного впечатления. Тем не менее математиков не оставляли сомнения в правильности такого рода доказательств, а иногда даже и получаемых с их помощью результатов. Общее отношение математиков к узакониванию научного статуса тех разновидностей чисел (иррациональных, отрицательных и комплексных), которые доставляли им столько хлопот, отчетливо выразил Д'Аламбер в своей статье об отрицательных числах, написанной для «Энциклопедии». В целом эта статья была написана недостаточно ясно и завершалась следующим признанием: «Алгебраические правила действий над отрицательными числами ныне общеприняты, и все признают их точными независимо от того, что бы мы ни думали о природе этих чисел». За многие века, на протяжении которых европейские математики упорно пытались понять природу различных типов чисел, на передний план выступила еще одна фундаментальная логическая задача — задача обоснования алгебры. Первой работой, существенно упорядочившей новые результаты, было «Великое искусство» Дж. Кардано. В этой книге Кардано показал, как решать кубические уравнения (например, x3 + 3x2 + 6x = 10) и уравнения четвертой степени (типа х4 + 3x3 + 6x2 + 7x + 5 = 0). Примерно за сто лет арсенал алгебры пополнился многими важными результатами, часть которых была известна еще арабским математикам: методом математической индукции, биномиальной теоремой и приближенными методами вычисления корней уравнений разных степеней. Основной вклад в сокровищницу алгебры внесли Виет, Гарриот, Жирар, Ферма, Декарт и Ньютон. Но все эти новые результаты фактически не были доказаны. Правда, Кардано, а позднее Бомбелли и Виет привели в обоснование своих методов решения кубических уравнений и уравнений четвертой степени кое-какие геометрические соображения, но, поскольку эти математики игнорировали отрицательные и комплексные корни, приведенные ими соображения заведомо не могли рассматриваться как доказательства. Кроме того, появление уравнений высших степеней, например четвертой и пятой, означало, что геометрия, ограниченная в те времена трехмерным пространством, не могла служить основой доказательств. Результаты, полученные другими авторами, чаще всего оказывались всего лишь более или менее удачными догадками, подсказанными конкретными примерами. Шаг в правильном направлении сделал Виет. Со времен Древнего Египта и Вавилона и вплоть до появления работы Виета математики решали уравнения первой степени, квадратные, кубические и уравнения четвертой степени, ограничиваясь всякий раз лишь какими-либо конкретными числовыми значениями коэффициентов. При подобном подходе уравнения 3x2 + 5x + 6 = 0 и 4x2 + 7x + 8 = 0 считались различными, хотя было ясно, что оба уравнения решаются одним и тем же методом. Кроме того, ученые стремились избежать отрицательных чисел; поэтому такое, например, уравнение, как x2 − 7x + 8 = 0, принято было записывать в виде x2 + 8 = 7x. Возникало множество типов уравнений одной и той же степени, каждый из которых приходилось рассматривать в отдельности. Главный вклад Виета в развитие алгебры состоял в введении буквенных коэффициентов. По образованию и роду занятий Виет был юристом; математика же была для него «хобби», которому он посвящал свободное от работы время, печатая и рассылая свои работы за собственный счет. Отдельные математики использовали буквенные обозначения и до Виета, но делали это лишь от случая к случаю. Виет был первым, кто продуманно ввел буквенные обозначения и систематически их использовал. Основное новшество состояло в том, что буквами обозначались не только неизвестные или степени неизвестных, но, как правило, и коэффициенты уравнений. Такой подход позволял единообразно рассматривать все квадратные уравнения, записав их (в современных обозначениях) в виде ax2 + bx + c = 0, где буквенные коэффициенты a, b и c могут означать любые числа, а x —неизвестную величину (или неизвестные величины), значения которой требуется найти. Виет назвал свою новую алгебру logistica speciosa (исчисление типов), противопоставляя ее тому, что он назвал logistica numerosa (исчисление чисел). Он хорошо понимал, что изучение квадратного уравнения общего вида ax2 + bx + c = 0 эквивалентно изучению всего класса квадратных уравнений. Проводя в своем сочинении «Введение в аналитическое искусство» (In artem analyticam isagoge, 1591) различие между logistica numerosa и logistica speciosa, Виет обозначил границу между арифметикой и алгеброй. По его словам, алгебра — это метод, позволяющий производить действия над типами или видами, т.е. logistica speciosa; арифметика же и теория решений уравнений с конкретными числовыми коэффициентами образуют logistica numerosa. Тем самым Виет возвел алгебру на более высокий уровень, превратив ее в науку об общих типах форм и уравнений: ведь результат, полученный в общем случае, охватывает бесконечно много частных случаев. Основное достоинство предложенных Виетом буквенных обозначений для классов чисел состояло в том, что, доказав правильность метода решения уравнения ax2 + bx + c = 0, математики могли с полным основанием применять тот же метод к решению бесконечно большого числа конкретных уравнений, например уравнения 3x2 + 7x + 5 = 0. Можно сказать, что основной вклад Виета в развитие алгебры состоит в придании общности алгебраическим доказательствам. Но чтобы производить какие-то операции над a, b и c, где a, b и c — любые вещественные или комплексные числа, необходимо быть уверенным в применимости этих операций ко всем вещественным и комплексным числам. А поскольку не только операции не были логически обоснованы, но даже определения различных типов чисел были достаточно расплывчаты, обоснование операций, производимых над буквами a, b и c в общем виде, заведомо были недостижимой целью. Сам Виет отвергал отрицательные и комплексные числа; поэтому общность, которой он достиг в logistica speciosa, была довольно ограниченной. Ход мысли Виета непостижим, если даже не иррационален. С одной стороны, Виет внес весьма существенный вклад, введя буквенные коэффициенты, и полностью сознавал важность этого шага, открывшего возможность получать общие доказательства. Вместе с тем Виет не признавал отрицательных чисел и отказывался придавать отрицательные значения буквенным коэффициентам — поистине и лучшие умы человечества могут страдать ограниченностью! Между тем правила действий над отрицательными числами существовали уже порядка 800 лет и всегда приводили к правильным результатам. Виет не мог игнорировать эти правила, которыми исчерпывалось почти все, чем располагала в его время алгебра. Но отрицательным числам недоставало наглядности и физического смысла, которыми обладали положительные числа. Лишь в 1657 г. Иоганн Худде (1633-1704) расширил область допустимых значений буквенных коэффициентов так, что она стала охватывать как отрицательные, так и положительные числа. Впоследствии его примеру последовало большинство математиков. Во времена Виета (в конце XVI в.) алгебра была лишь скромным придатком геометрии. Алгебраисты занимались решением либо одного уравнения с одним неизвестным, либо решением двух уравнений с двумя неизвестными — задачи такого рода возникали в связи с практическими проблемами геометрии или торговли. Могущество алгебры оставалось скрытым вплоть до XVII в. Решающий шаг был сделан Рене Декартом и Пьером де Ферма, создавшими аналитическую геометрию (которую следовало бы называть алгебраической геометрией, если бы ныне этот термин не приобрел совсем другого смысла{75}). Основная идея новой науки состояла в том, что если на плоскости задать систему координат, то каждой кривой можно сопоставить ее уравнение. Например, уравнение х2 + y2 = 25 соответствует окружности радиуса 5 с центром в начале координат. Использование уравнений позволяет доказывать всевозможные свойства кривой гораздо проще, чем чисто геометрические (или синтетические) методы античных математиков. Но в 1637 г., когда Декарт опубликовал свою «Геометрию», ни он сам, ни Ферма в работе 1629 г. (опубликованной посмертно) не были подготовлены к тому, чтобы принять отрицательные числа. Им обоим была ясна идея алгебраического подхода к геометрии, но ни тот, ни другой еще не представляли, сколь широки возможности такого подхода. Отрицательные числа были введены в аналитическую геометрию потомками Декарта и Ферма, и она стала играть весьма важную роль в главных событиях, происходивших в математическом анализе и в геометрии. Представление функций алгебраическими формулами было вторым новшеством, выдвинувшим алгебру на первый план. Как известно (гл. II), идею описания движений с помощью формул выдвинул Галилей. Так, тело, брошенное вверх со скоростью 30 м/с, через t с будет находиться над поверхностью Земли на высоте h, определяемой формулой h = 30t − 4,9t2 м. Из этой формулы с помощью чисто алгебраических средств можно извлечь неисчерпаемое количество сведений о движении: например, установить максимальную высоту подъема; время, необходимое для подъема на максимальную высоту; время, необходимое для падения с максимальной высоты на землю. Вскоре математики сознали могущество алгебры, которая заняла господствующее положение в математике, оттеснив геометрию на второй план. Безграничное применение алгебры вызвало множество протестов. Философ Томас Гоббс был в математике величиной далеко не первого порядка, тем не менее именно он выразил мнение многих математиков, выступив с протестом против «несметного полчища тех, кто применяет алгебру к геометрии». Гоббс утверждал, что алгебраисты ошибочно подменяют геометрию символами, и отозвался о книге Джона Валлиса по аналитической геометрии конических сечений как о «гнусной книге», покрытой «паршой символов». Против применения алгебры выступали многие видные математики, в том числе Блез Паскаль и Исаак Барроу; при этом они ссылались на то, что алгебра логически не обоснована, и по той же причине настаивали на чисто геометрических методах и доказательствах. Кое-кто из математиков полагал, будто отступление на позиции геометрии позволит логически обосновать алгебру (как мы уже отмечали, подобная позиция была ошибочной). Но большинство математиков свободно применяли алгебру в чисто утилитарных целях. Ценность алгебры состояла в том, что она равно хорошо (как и геометрия) позволяла решать все те задачи, с которыми сталкивались математики, а превосходство алгебры даже при рассмотрении чисто геометрических проблем было столь очевидно, что математики бесстрашно погрузились в ее воды. В отличие от Декарта, считавшего алгебру служанкой геометрии, Джон Валлис и Ньютон полностью сознавали силу алгебраических методов. И все же математики весьма неохотно отказались от геометрических подходов. По свидетельству Генри Пембертона, выпустившего третье издание ньютоновских «Начал», Ньютон не только постоянно выражал свое восхищение древнегреческой геометрией, но и сетовал на себя за то, что не следовал примеру античных математиков в большей мере. В письме к Дэвиду Грегори (1661-1708), племяннику Джеймса Грегори (1638-1675), Ньютон заметил: «Алгебра — это анализ для неумех в математике». Но в своей «Всеобщей арифметике» (1707) он приложил максимум усилий, чтобы убедительно показать превосходство алгебры. Арифметику и алгебру Ньютон излагал как основу математики, обращаясь к геометрии лишь в тех случаях, когда ему требовалось доказать то или иное утверждение. Тем не менее в целом «Всеобщая арифметика» была не более чем набором правил. Утверждения о числах или алгебраических методах лишь изредка подкреплялись доказательствами или интуитивными соображениями. По мнению Ньютона, буквы в алгебраических выражениях означают числа, а в достоверности арифметики никто не может усомниться. Лейбниц также отметил все возрастающую главенствующую роль алгебры и по достоинству оценил эффективность алгебраических методов. По поводу замечаний некоторых математиков о том, что алгебраические утверждения не подкреплены доказательствами, Лейбниц счел нужным заявить: «Геометрам нередко удается несколькими словами выразить то, что требует громоздких рассуждений в анализе… применимость алгебры не вызывает сомнений, но с доказательностью у нее не все благополучно». Работу в современной ему алгебре Лейбниц назвал «смесью удачи и счастливого случая». Однако Леонард Эйлер в своем «Введении в анализ бесконечно малых» (1748) открыто и безоговорочно провозгласил превосходство алгебры над геометрическими методами греков. К середине XVIII в. сдержанное отношение к применению алгебры было окончательно преодолено. К тому времени алгебра напоминала раскидистое дерево с множеством ветвей, но почти полностью лишенное корней. Развитие числовых систем и алгебры разительно отличается от развития геометрии. К III в. до н.э. геометрия имела уже дедуктивный характер. Немногие обнаружившиеся в ней пробелы и изъяны, как мы увидим в дальнейшем, оказались легко поправимыми. Что же касается арифметики и алгебры, то они никогда не были логически обоснованы. Казалось бы, отсутствие логического обоснования должно вызывать тревогу у всех математиков. Как могли европейцы, до тонкости изучившие дедуктивную геометрию греков, принять и применять различные типы чисел и алгебру, никогда не имевшие логического обоснования? Можно назвать несколько причин. Основой принятия целых чисел и дробей, несомненно, был накопленный опыт. Когда же числовая система пополнилась новыми типами чисел, правила арифметических действий, принятые на эмпирической основе для положительных целых чисел и дробей, были распространены на новые элементы, а в случае затруднений на выручку безотказно приходило геометрическое мышление. Буквенные символы лишь заменяли числа — и поэтому с ними можно было обращаться так же, как с числами. Более сложные алгебраические методы казались обоснованными либо с помощью геометрических соображений типа тех, которые в свое время использовал Кардано, либо — в отдельных частных случаях — с помощью одной лишь индукции. Разумеется, ни тот, ни другой подход не был логически удовлетворительным. Геометрия даже в тех случаях, когда к ней обращались, не позволяла логически обосновать введение отрицательных, иррациональных и комплексных чисел. По очевидным причинам решение уравнения четвертой степени невозможно обосновать геометрически. Кроме того, сначала, особенно в XVI-XVII вв., алгебру не считали независимой областью математики, которая нуждалась в особом логическом обосновании. Алгебру принято было рассматривать как метод анализа геометрических задач. Многие из тех, кто широко использовал алгебру, прежде всего Декарт, считали ее не более чем методом анализа. Название сочинений Кардано «Великое искусство» и Виета «Введение в аналитическое искусство» свидетельствуют о том, что их авторы использовали слово «искусство» в смысле, встречавшемся иногда и в наши дни, — как некую противоположность науке. Название «аналитическая геометрия», закрепившееся за координатной геометрией Декарта, подтверждает отношение к алгебре как к методу анализа. Еще в 1704 г. Эдмонд Галлей в статье, опубликованной в журнале Philosophical Transactions of the Royal Society, говорил об алгебре как об аналитическом искусстве. Но аналитическая геометрия Декарта стала, по-видимому, тем решающим доводом, который убедил математиков в могуществе алгебры. Наконец, нельзя не упомянуть и о том, что использование для обработки результатов научных исследований отрицательных и иррациональных чисел, а также алгебры приводило к превосходному согласию с результатами наблюдений и экспериментов. Какие бы сомнения ни испытывали математики, применяя отрицательные числа в естественнонаучных исследованиях, все сомнения следовало отбросить, как только окончательный результат оказывался физически правильным: ведь математики заботились главным образом о естественнонаучных приложениях — и все, что доказывало свою полезность на деле, принималось без особого разбора. Запросы естествознания ставились превыше логической обоснованности. Сомнения в правильности алгебры были просто-напросто отметены, подобно тому как ненасытные промышленники зачастую отметали этические принципы; математики стали применять новую алгебру с радостью и уверенностью в своей правоте. Впоследствии математики шаг за шагом превратили алгебру в независимую науку, охватывающую и числа, и геометрию и позволяющую «доказывать» новые результаты. Так, Валлис утверждал, что алгебраические методы ничуть не менее законны, чем геометрические. К концу XVII в. математики осознали, что арифметика и алгебра независимы от геометрии. Почему же математики не предприняли попыток логически обосновать и то, и другое? Почему, имея перед собой высокий образец дедуктивного изложения геометрии, воплощенный в «Началах» Евклида, математики не попытались изложить аналогичным образом арифметику и алгебру? Ответ состоит в том, что геометрические понятия, аксиомы и теоремы интуитивно воспринимаются намного легче, чем понятия арифметики и алгебры. Наглядные образы, «картинки» (в случае геометрии — чертежи), облегчают математику понимание той или иной структуры. Понятия же иррационального, отрицательного или комплексного числа отличаются большей тонкостью, и даже «картинки», которые появились здесь позднее, не позволяют прочувствовать логическую организацию самих чисел или буквенных выражений, оперирующих с числами. Проблема поиска логического обоснования числовой системы и алгебры была трудной, гораздо более трудной, чем могли себе представить математики XVII в. В дальнейшем (гл. VIII) нам еще представится случай вернуться к этой проблеме. К счастью, в вопросах логического обоснования арифметики и алгебры математики оказались скорее легковерными и даже наивными, чем излишне педантичными, — к счастью, ибо формализации и логическому обоснованию должен предшествовать период созидания, не стесняемого никакими ограничениями, а величайший период созидания в математике уже приближался. 60. Платон делил Вселенную на «мир видимый», куда относится все реально существующее и «мир умопостижимый», но не видимый и не осязаемый, к которому он относил, в частности, математику и искусство [см., например, «Государство» Платона ([7], с. 317 и далее)]. 61. Как мы уже отмечали, Евклид, следуя математическим установкам Аристотеля, пытался обойтись в геометрии без всякого использования движений (что ему, кстати сказать, полностью так и не удалось). 62. Любое нечетное число представимо в виде 2n + 1, где n — некоторое целое число. Квадрат нечетного числа (2n + 1)2 = 4n2 + 4n + 1 = 2(2n2 + 2n) + 1 — нечетное число. 63. Своеобразным отражением этого является, в частности, тот факт, что в «Началах» так называемый алгоритм Евклида в одинаковых выражениях описывается два раза: один раз — для чисел и второй раз — для отрезков. 64. Возможно, эту формулу знал еще Архимед. — Ред. 65. За единицу площади здесь принимается квадрат со стороной, равной единице длины. — Ред. 66. Формулы для решения в целых числах «пифагорова уравнения» x2 + y2 = z2 обычно приписываются Платону, но реально они, безусловно, были известны ранее, скажем в школе пифагорейцев. Выдающийся знаток вавилонской математики, ученик Д. Гильберта Отто Нейгебауэр (р. 1899) предположил даже, что эти формулы (разумеется, без строго логического их обоснования) были известны еще в древнем Вавилоне, ибо иначе становится совершенно загадочной обнаруженная Нейгебауэром древневавилонская клинописная глиняная табличка, содержащая список ряда первых решений этого уравнения. 67. Диофантовым анализом (см. по этому поводу: Башмакова и Славутин [34]) обычно называют теорию решений неопределенных уравнений (т.е. уравнений, содержащих более одного переменного) в целых числах, тогда как Диофанта интересовала родственная проблема отыскания рациональных решений подобных уравнений. 68. Почти одновременно с шотландцем Джоном Непером и независимо от него к идее логарифмов пришел швейцарский часовщик Иобст Бюрги (1552-1632). 69. Теория Евдокса — Евклида содержала почти безупречное определение иррациональных чисел (которым придавалось обличие отношений отрезков) и условий их равенства — но, разумеется, проблемы логического обоснования действий над иррациональными числами здесь не были доведены до того уровня, который приобрели они в математике 2-й половины XIX в. 70. Любопытно, что открытая Декартом и по сей день сохранившая его имя кривая, описываемая уравнением x3 + y3 − 3xy = 0, ныне рисуется вовсе не так, как это делал Декарт, считавший, что x и y должны быть только положительными; при этом мы по-прежнему называем эту кривую «декартов лист», хотя, если не ограничиваться одними лишь положительными значениями абсциссы и ординаты, рассматриваемая кривая утрачивает форму листа, какую она имела на чертежах Декарта. 71. В этой связи уместно вспомнить строки из У.Г. Одена: «Минус на минус — всегда только плюс. Отчего так бывает, сказать не берусь». 72. Так называемая формула Кардано для корня (точнее, для трех корней) кубического уравнения x3 + px + q = 0 (найдена она была несколько раньше, но опубликована впервые в «Великом искусстве» Кардано, который, впрочем, и не претендовал здесь на приоритет) имеет вид: 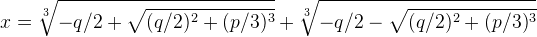 при этом если все три корня уравнения являются вещественными (неприводимый случай решения рассматриваемого уравнения), то (q/2)2 + (p/3)3 < 0 — и правильный ответ можно получить из этой формулы лишь при умении извлекать кубические корни из комплексных чисел (как это сделать, впервые объяснил Р. Бомбелли). 73. Характерно, что при всей глубине и тонкости мысли, отражением которых явились статьи «Предел» и «Дифференциал» в знаменитой «Энциклопедии» (по существу впервые обосновавшие математический анализ почти на уровне построений Огюстена Коши) или статья «Размерность» (впервые провозгласившая, что мы живем в четырехмерном мире: три измерения — пространственные, четвертое — временное), к вопросу о введении в математику отрицательных чисел Д'Аламбер подходил с большой робостью, а комплексные числа вообще полностью игнорировал. 74. Эйлер использует здесь так называемую тригонометрическую, или полярную, форму комплексного числа; здесь ρ = √(x2 + y2), φ — угол, образуемый с положительным направлением оси x отрезком, проведенным из начала координат в точку x + iy (при y = 0, угол φ также равен 0). При этом x + iy = ρ(cos φ + ί sin φ) = ρeiφ. 75. Впрочем, многие современные математики, скажем Жан Дьедонне (род. в 1906 г.), возражают и против традиционного употребления термина аналитическая геометрия, придавая ему смысл, логически вытекающий из современного понимания термина алгебраическая геометрия (алгебраическая и аналитическая геометрия по Дьедонне — это учение об алгебраических, соответственно аналитических многообразиях в многомерном пространстве); поэтому созданную Декартом и Ферма область математики следовало бы, пожалуй, называть координатной геометрией.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ V. Нелогичное развитие логичнейшей из наук / Математика. Утрата определенности // Морис Клайн |
|
[time: 9 ms; queries: 7]
1 Фев 2026 11:16:06 GMT+3 |


 На протяжении двух тысячелетий математики были уверены в том, что весьма успешно открывают математические принципы, заложенные в фундаменте мироздания. Но в середине XIX в. они вынуждены были признать, что глубоко заблуждались, принимая математические законы за абсолютные истины. В течение двух тысячелетий математики не сомневались, что неукоснительно следуют предложенной древнегреческими мыслителями схеме постижения истины, выводя с помощью дедуктивных рассуждений из математических аксиом следствия, не уступающие по надежности самим исходным аксиомам. Поскольку математические законы естествознания отличались необычайной точностью, редкие расхождения по поводу корректности некоторых математических рассуждений от «метались как не заслуживающие внимания. Даже самые проницательные и дальновидные математики были убеждены, что любой пробел в математическом доказательстве, если таковой обнаружится, может быть легко восполнен. Но в XIX в. единодушие математиков по поводу безупречной доказательности математических рассуждений явно поколебалось.
На протяжении двух тысячелетий математики были уверены в том, что весьма успешно открывают математические принципы, заложенные в фундаменте мироздания. Но в середине XIX в. они вынуждены были признать, что глубоко заблуждались, принимая математические законы за абсолютные истины. В течение двух тысячелетий математики не сомневались, что неукоснительно следуют предложенной древнегреческими мыслителями схеме постижения истины, выводя с помощью дедуктивных рассуждений из математических аксиом следствия, не уступающие по надежности самим исходным аксиомам. Поскольку математические законы естествознания отличались необычайной точностью, редкие расхождения по поводу корректности некоторых математических рассуждений от «метались как не заслуживающие внимания. Даже самые проницательные и дальновидные математики были убеждены, что любой пробел в математическом доказательстве, если таковой обнаружится, может быть легко восполнен. Но в XIX в. единодушие математиков по поводу безупречной доказательности математических рассуждений явно поколебалось.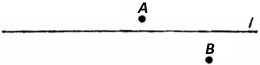
 Книга известного американского математика и логика профессора Р. Смаллиана, продолжающая серию книг по занимательной математике, посвящена логическим парадоксам и головоломкам, логико-арифметическим задачам и проблемам разрешимости, связанным с теоремой Геделя. Рассчитана на интересующихся занимательной математикой.
Книга известного американского математика и логика профессора Р. Смаллиана, продолжающая серию книг по занимательной математике, посвящена логическим парадоксам и головоломкам, логико-арифметическим задачам и проблемам разрешимости, связанным с теоремой Геделя. Рассчитана на интересующихся занимательной математикой. Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности.
Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности. Теорема Гёделя, наряду с открытием теории относительности, квантовой механики и ДНК, обычно рассматривается как крупнейшее научное достижение ХХ века. Почему? В чем ее суть? Каково ее значение? Эти вопросы в своей лекции раскрывает Алексей Брониславович Сосинский, математик, профессор Независимого московского университета, офицер Ордена академических пальм Французской Республики, лауреат премии Правительства РФ в области образования 2012 года. В частности, были даны несколько разных ее формулировок, описаны три подхода к ее доказательству (Колмогорова, Чейтина и самого Гёделя), и объяснено ее значение для математики, физики, компьютерной науки и философии.
Теорема Гёделя, наряду с открытием теории относительности, квантовой механики и ДНК, обычно рассматривается как крупнейшее научное достижение ХХ века. Почему? В чем ее суть? Каково ее значение? Эти вопросы в своей лекции раскрывает Алексей Брониславович Сосинский, математик, профессор Независимого московского университета, офицер Ордена академических пальм Французской Республики, лауреат премии Правительства РФ в области образования 2012 года. В частности, были даны несколько разных ее формулировок, описаны три подхода к ее доказательству (Колмогорова, Чейтина и самого Гёделя), и объяснено ее значение для математики, физики, компьютерной науки и философии. В этой книге говориться о математике как о части культуры духовной. Данный текст писался не для математиков, а скорее для гуманитариев. Поэтому при его составлении в ряде случаев приходилось выбирать между понятностью и точностью. Предпочтение отдавалось понятности. Очерчивая место математики в современной культуре, автор пытается прояснить для читателей-нематематиков некоторые основные понятия и проблемы «царицы наук».
В этой книге говориться о математике как о части культуры духовной. Данный текст писался не для математиков, а скорее для гуманитариев. Поэтому при его составлении в ряде случаев приходилось выбирать между понятностью и точностью. Предпочтение отдавалось понятности. Очерчивая место математики в современной культуре, автор пытается прояснить для читателей-нематематиков некоторые основные понятия и проблемы «царицы наук». Книга известного американского ученого, почетного профессора математики Нью-Йоркского университета, популяризатора науки Мориса Клайна ярко и увлекательно рассказывает о роли математики в сложном многовековом процессе познания человеком окружающего мира, ее места в физических науках. Имя автора давно и хорошо известно советским и российским читателям.
Книга известного американского ученого, почетного профессора математики Нью-Йоркского университета, популяризатора науки Мориса Клайна ярко и увлекательно рассказывает о роли математики в сложном многовековом процессе познания человеком окружающего мира, ее места в физических науках. Имя автора давно и хорошо известно советским и российским читателям. Мэрилин вос Савант, рекордсмен мира по IQ — 228 пунктов, — не внесла ничего ни в науку, ни в искусство, а всего лишь ведет колонку вопросов и ответов в журнале Parade. Самые что ни на есть посредственные физики обладают гораздо более высоким коэффициентом интеллекта, чем лауреат Нобелевской премии Ричард Фейнман, которого многие считают последним величайшим американским гением (его IQ составлял «всего лишь» приличные 122 пункта). Исследователи давно пытаются установить взаимосвязь между интеллектом и гением, но интеллекта оказывается явно недостаточно. В издательстве МИФ вышла книга «Взлом креатива» американского эксперта по креативности Майкла Микалко с примерами из работ известных мыслителей и практическими упражнениями по поиску оригинальных идей. Публикуем некоторые главы.
Мэрилин вос Савант, рекордсмен мира по IQ — 228 пунктов, — не внесла ничего ни в науку, ни в искусство, а всего лишь ведет колонку вопросов и ответов в журнале Parade. Самые что ни на есть посредственные физики обладают гораздо более высоким коэффициентом интеллекта, чем лауреат Нобелевской премии Ричард Фейнман, которого многие считают последним величайшим американским гением (его IQ составлял «всего лишь» приличные 122 пункта). Исследователи давно пытаются установить взаимосвязь между интеллектом и гением, но интеллекта оказывается явно недостаточно. В издательстве МИФ вышла книга «Взлом креатива» американского эксперта по креативности Майкла Микалко с примерами из работ известных мыслителей и практическими упражнениями по поиску оригинальных идей. Публикуем некоторые главы. Теплым весенним утром Джун Ху шел в зал Макдоннелла Пристонского университета, где его ждали студенты. Однако он не был уверен, что идет в нужном направлении. Ху работает в элитарном Институте перспективных исследований, который располагается неподалеку от студгородка Принстона. Будучи сотрудником института, Ху не обязан преподавать. Тем не менее, он вызвался прочитать студентам продвинутый курс по коммутативной алгебре.
Теплым весенним утром Джун Ху шел в зал Макдоннелла Пристонского университета, где его ждали студенты. Однако он не был уверен, что идет в нужном направлении. Ху работает в элитарном Институте перспективных исследований, который располагается неподалеку от студгородка Принстона. Будучи сотрудником института, Ху не обязан преподавать. Тем не менее, он вызвался прочитать студентам продвинутый курс по коммутативной алгебре.