|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Видео ≫ Второй закон термодинамики в квантовом мире // Гордей Лесовик |
Второй закон термодинамики в квантовом миреГордей Лесовик
Если попросить любого профессионального физика коротко ответить на вопрос о том, выполняется ли в квантовом мире первый закон термодинамики или закон сохранения энергии, то, конечно, он ответит «да». Но если попросить его рассказать поподробнее, то возникнут нюансы, которые описываются соотношением неопределенностей Гейзенберга. Оказывается, что если наблюдать систему короткое, конечно, время, тогда энергия не совсем определена и степень ее неопределенности дается соотношением ΔE порядка ħ (постоянная Планка) поделить на время. Такого же качественного смысла отклонения имеются и во втором законе термодинамики. На коротких временах могут возникать флуктуации, приводящие к уменьшению энтропии или к неправильным потокам тепла. Это называется флуктуационная теорема, которая количественно описывает эти процессы. Более интересно то, что происходит на сколь угодно длинных временах в постоянном режиме. Некоторое время назад мы с группой соавторов начали выводить второй закон термодинамики с точки зрения квантовой механики. Например, в одной из его формулировок, гласящей, что энтропия замкнутой системы не убывает, типично растет, а иногда остается постоянной, если система энергетически изолирована. Используя известные результаты квантовой теории информации, мы вывели некоторые условия, при которых это утверждение справедливо. Неожиданно выяснилось, что эти условия не совпадают с условием энергетической изолированности систем. При этом возникает качественная картина. Она возникает таким образом, что система, изначально не скоррелированная с резервуаром, взаимодействует с ним, хотя и почти без передачи энергии. Возникают явления так называемой запутанности — знаменитая ЭПР-корреляция, открытая Эйнштейном, Подольским и Розеном. Говоря более старым языком, возникают сбои фазы в системе, и система приходит в неупорядоченное состояние, когда уже невозможно предсказать вероятность ее состояния, в отличие от исходного состояния. Мы показали, что для ряда систем второй закон выполняется, энтропия растет, если система энергетически изолирована или квазиизолирована от резервуара. Это и есть главный результат нашей работы, опубликованной в 2016 году. Но он интересен с академической точки зрения и как таковой вызвал не слишком много интереса. Интерес вызвали те случаи, когда формулировка второго закона оказывалась неверной. Энергетически изолированная система, оказывается, может испытывать такую эволюцию, при которой энтропия убывает. Причиной этого по-прежнему является квантовая запутанность, но она должна быть специальным образом аранжированная. Она должна быть, во-первых, сильная, во-вторых, оператор, который описывает взаимодействие системы и резервуара, в зависимости от переменных, описывающих состояние системы и резервуара, должен не коммутировать. Эти компоненты должны не коммутировать между собой. Может быть, не все знают, что такое коммутация. Простой пример, который придумал один из моих соавторов: если надеть на себя сначала рубашку, а потом свитер, а потом сделать наоборот — сначала надеть свитер, а потом рубашку, — разница в ощущениях будет. Эта разница в ощущениях и есть коммутатор. В общем, если есть разница в последовательности применения операторов, то они коммутируют. Когда мы поняли, что условия выполнения второго закона не совпадают с условием квазиизолированности по энергии, мы начали искать, в каких случаях бывает так, что энергетическая изолированность есть, а энтропия убывает. Эти случаи можно описать на языке спинов, кубитов. Если специальным образом приготовить низкоразмерные системы, тогда резервуар будет в так называемом чистом квантово-механическом состоянии. Можно придумать такое взаимодействие, при котором система изначально будет в максимально неупорядоченном состоянии, а после взаимодействия с некоторым кусочком резервуара очистится. Система перейдет в так называемое чистое квантово-механическое состояние, в основное состояние, а кусок резервуара станет максимально неупорядоченным. То есть перейдем в максимально неупорядоченное состояние. Тогда мы поняли, что действие такого куска резервуара очень похоже на действие демона Максвелла. Только демон Максвелла обменивался информацией с системой, он узнавал, в каком она состоянии, и что-то с ней делал, а здесь это происходит без обмена информацией. На языке квантовой информатики эта операция может быть описана для кубитов как своп-операция. Мы начали с этим разбираться и выяснили, что люди уже занимались этой темой с квантово-информационной стороны. Они не очень следили за сохранением энергии. Для них энергия не очень интересный параметр, но тем не менее что-то на эту тему известно. Например, Сет Ллойд писал про квантовых демонов Максвелла. Следующий вопрос. Хорошо, энтропия может убывать. В классической формулировке термодинамики есть три эквивалентных формулировки: энтропия не убывает, растет или константна; тепло всегда передается от горячего к холодному телу; тепло от горячего источника невозможно полностью, на 100% перевести в работу. КПД теплового двигателя не может быть 100%. В квантовом случае возникает вопрос, можно ли из убывания энтропии сделать такой холодильник, который сам по себе передавал бы от холодного к горячему, или вечный двигатель второго рода. Тепловая машина с КПД 100% — это и есть вечный двигатель второго рода. Теоретически это можно, мы это и описали. Вечный двигатель второго рода пока не реализован экспериментально, хотя установка, когда энтропия убывает, уже реализована французскими экспериментаторами. Она, к сожалению, реализована в таком режиме, когда квантовый демон очень близко к системе. А в случае, если мы объединим и квантового демона, и систему, то в сумме второй закон не нарушается, ничего интересного. Чтобы было интересно, их нужно разнести. Эту ситуацию мы сейчас описываем теоретически. Надеемся, что ее получится подтвердить экспериментально. Пока что мы разрабатываем теорию о нарушении формулировки, связанной с убыванием энтропии, а в будущем планируем создать теорию и по извлечению работы. То, что мы сумели описать теоретически, — это стопроцентная концентрация энергии, извлеченной из теплового источника. Теоретически мы умеем концентрировать энергию. Мы можем запасти энергию в квантовой батарейке. Энергия будет возбужденным кубитом или будет существовать в фотонах, но стопроцентно превращать эту энергию в работу мы не умеем. Это не наш недостаток, у всех не получается. Если у нас есть электрическая батарейка и она на 100% заряжена, всю ее энергию не получается превратить в работу, она где-то диссипирует. Это немного другой вопрос, но тем не менее такая проблема есть, над ней мы тоже работаем. Есть еще один вариант нарушения второго закона. Когда мы выводили из квантовой механики свойство роста энтропии, важно было условие, что изначально система не скоррелирована с резервуаром. Дело в том, что если это не так, то может происходить противоположный процесс, то есть энтропия начнет убывать. Это относится к знаменитому парадоксу Лошмидта. На самом деле это описывал еще лорд Кельвин в XIX веке. Загадка состояла в том, что известно, что есть второй закон, была открыта H-теорема Больцмана, которая говорит о том, что если система подчиняется кинетическому уравнению — а это можно некоторым образом оправдать, — тогда энтропия системы все время растет или она константна. Но микроскопические законы, в частности законы классической механики, симметричны по времени. Спрашивается: откуда взялась эта стрела времени? Почему это так? Больцман правильно ответил на этот вопрос. Он сказал, что создать такие начальные условия, при которых эволюция пойдет вспять, очень сложно. Это сейчас понятно и с точки зрения квантовой механики. Для маленьких систем уже научились создавать такие хитрые условия, что сначала система будет эволюционировать так, что энтропия будет расти, она будет запутываться, начинать коррелироваться с резервуаром, а потом мы делаем некоторое хитрое действие, почти магическое, квантовое, и она начинает крутиться обратно, вспять во времени и возвращается в исходное состояние. Над этим мы сейчас активно работаем и придумываем такие алгоритмы, чтобы сделать это в максимально более сложной ситуации. Это тоже один из вариантов нарушения второго закона термодинамики. В те времена о том, что система может быть скоррелирована с резервуаром, да еще квантовым образом, даже не думали. Но если об этом думать, то могут происходить удивительные вещи, опять же нарушающие стандартные представления о втором законе термодинамики. Резюмируя, я бы сказал, что многие критикуют такую деятельность, говоря, что нельзя пытаться применять законы термодинамики, которые применимы к большим объектам, к квантово-механическим маленьким объектам. Но оказывается, что можно. Мы показали, что в типичном случае квантовая механика оправдывает второй закон термодинамики, его можно вывести. И он работает даже для маленьких систем. Нарушение и какие-то хитрости начинаются, если очень сильно постараться, специальным образом сделать систему, кусочек резервуара, заставив их взаимодействовать особым образом. В типичном случае даже для микромира второй закон термодинамики во всех его трех формулировках вполне выполняется. И квантовая механика, которая за весь мир и ответственна, его описывает. Гордей Лесовик, доктор физико-математических наук, ведущий научный сотрудник Института теоретической физики им. Л.Д. Ландау. ПостНаука
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Видео ≫ Второй закон термодинамики в квантовом мире // Гордей Лесовик |
|
[time: 11 ms; queries: 7]
10 Мар 2026 22:01:03 GMT+3 |


 Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.
Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание. Возникновение сложного из простого — это, казалось бы, злостное нарушение второго закона термодинамики. Второй закон требует постепенного выравнивания градиентов, разупорядочивания элементов и увеличения энтропии в системе. Тем не менее жизнь так специально устроена, чтобы поддерживать градиенты, упорядочивать элементы и уменьшать энтропию. Эти принципы справедливы как для одного организма, так и для целых экосистем, биот, эволюционных последовательностей. Значит ли это, что жизнь действительно противоречит законам физики?
Возникновение сложного из простого — это, казалось бы, злостное нарушение второго закона термодинамики. Второй закон требует постепенного выравнивания градиентов, разупорядочивания элементов и увеличения энтропии в системе. Тем не менее жизнь так специально устроена, чтобы поддерживать градиенты, упорядочивать элементы и уменьшать энтропию. Эти принципы справедливы как для одного организма, так и для целых экосистем, биот, эволюционных последовательностей. Значит ли это, что жизнь действительно противоречит законам физики?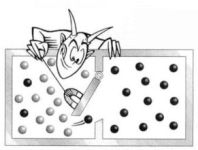 Теплота — вещь мистическая. Можно взять в руку кусок дерева, и от него руке не будет, по большому счету, ни тепло, ни холодно. Однако стоит бросить его в огонь — и оно, загоревшись, будет выделять теплоту в большом количестве. Откуда же берется теплота? Издревле люди считали, что теплота представляет собой особую жидкость под названием флогистон, или теплород, заключенную в дереве и других горючих субстанциях и высвобождающуюся при горении. Сегодня мы понимаем теплоту (точнее сказать, тепловую или термальную энергию) как особую форму энергии, связанную с движением атомов или молекул, из которых состоит материал. При притоке энергии извне атомы или молекулы разогреваются — т. е. начинают колебаться или двигаться быстрее, при остывании же движение замедляется.
Теплота — вещь мистическая. Можно взять в руку кусок дерева, и от него руке не будет, по большому счету, ни тепло, ни холодно. Однако стоит бросить его в огонь — и оно, загоревшись, будет выделять теплоту в большом количестве. Откуда же берется теплота? Издревле люди считали, что теплота представляет собой особую жидкость под названием флогистон, или теплород, заключенную в дереве и других горючих субстанциях и высвобождающуюся при горении. Сегодня мы понимаем теплоту (точнее сказать, тепловую или термальную энергию) как особую форму энергии, связанную с движением атомов или молекул, из которых состоит материал. При притоке энергии извне атомы или молекулы разогреваются — т. е. начинают колебаться или двигаться быстрее, при остывании же движение замедляется. Идеальный газ. Уравнение состояния газа. Взаимосвязь давления, температуры и объёма. Механизмы рождения макропараметров в рамках «молекулярного бильярда». Первое начало термодинамики как закон сохранения энергии. Вывод уравнения Бернулли. Энтропия и второе начало термодинамики. Тепловые машины и цикл Карно. Энтропия информационная. Энтропия как неопределённость. Аксиоматический подход к определению энтропии. Принцип максимума энтропии. Подход статистической физики за пределами термодинамики.
Идеальный газ. Уравнение состояния газа. Взаимосвязь давления, температуры и объёма. Механизмы рождения макропараметров в рамках «молекулярного бильярда». Первое начало термодинамики как закон сохранения энергии. Вывод уравнения Бернулли. Энтропия и второе начало термодинамики. Тепловые машины и цикл Карно. Энтропия информационная. Энтропия как неопределённость. Аксиоматический подход к определению энтропии. Принцип максимума энтропии. Подход статистической физики за пределами термодинамики. Энтропия — термин, которые слышали многие, а вот дать точное объяснение не каждому удастся. И в этом нет ничего удивительного, ведь наши познания о том, что нас окружает, как правило, очень поверхностны. Кто-то утверждает, что это разница между идеальным и реальным процессом. Но все же больше сходятся во мнении, что это мера хаоса. Ведь с самого детства нас приучают к порядку, отсюда и наполненность нашего мира флуктуациями и бифуркациями. Так к чему может привести война с энтропией? И нужна ли она вообще? Ведь если бы не хаос, сам мир бы не произошел…
Энтропия — термин, которые слышали многие, а вот дать точное объяснение не каждому удастся. И в этом нет ничего удивительного, ведь наши познания о том, что нас окружает, как правило, очень поверхностны. Кто-то утверждает, что это разница между идеальным и реальным процессом. Но все же больше сходятся во мнении, что это мера хаоса. Ведь с самого детства нас приучают к порядку, отсюда и наполненность нашего мира флуктуациями и бифуркациями. Так к чему может привести война с энтропией? И нужна ли она вообще? Ведь если бы не хаос, сам мир бы не произошел…