|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Законы термодинамики |
Законы термодинамики
Механическая теория теплоты Теплота представляет собой форму энергии, связанную с хаотичным движением атомов или молекул вещества. Теплота — вещь мистическая. Можно взять в руку кусок дерева, и от него руке не будет, по большому счету, ни тепло, ни холодно. Однако стоит бросить его в огонь — и оно, загоревшись, будет выделять теплоту в большом количестве. Откуда же берется теплота? Издревле люди считали, что теплота представляет собой особую жидкость под названием флогистон, или теплород, заключенную в дереве и других горючих субстанциях и высвобождающуюся при горении. К концу XVIII века, однако, накопилось достаточно экспериментальных данных, чтобы убедиться в ошибочности такой теории. Одним из первых современные представления о природе теплоты предложил Бенджамин Томпсон (граф Румфорд). Он всегда отличался техническим складом ума и интересовался наукой применительно к баллистике и оружейному делу, которым посвятил свою жизнь. Уже живя в Баварии, он был техническим управляющим пушечного завода. Грубо отлитые стволы обрабатывались изнутри сверлильной фрезой для доведения до нужного калибра и придания им должной гладкости. Румфорд заметил, что при расточке стволы нагреваются, причем тем сильнее, чем тупее фреза. Измерив теплоемкость металлической стружки, ему удалось показать, что тепло никак не могло храниться до расточки в веществе ствола, а следовательно, теплота возникает в результате трения. Рассказывают, что он даже помещал рассверливаемую пушку в воду и сверлил ее, пока вода не закипела спустя несколько часов. Сегодня мы понимаем теплоту (точнее сказать, тепловую или термальную энергию) как особую форму энергии, связанную с движением атомов или молекул, из которых состоит материал. При притоке энергии извне атомы или молекулы разогреваются — т. е. начинают колебаться или двигаться быстрее, при остывании же движение замедляется. В жидкостях и газах увеличивается скорость хаотичного броуновского движения и частота соударений атомов или молекул друг с другом. В твердых же телах атомы с большей амплитудой колеблются вокруг своих мест в кристаллической решетке. В обоих случаях, однако, то, что мы воспринимаем как теплоту или термальную энергию, на самом деле является кинетической энергией атомов или молекул. Как и все другие формы энергии, подчиняющиеся первому началу термодинамики, тепловая энергия может переходить в другие формы энергии, и это используется, например, в двигателях внутреннего сгорания и электрогенераторах. Молекулярно-кинетическая теория Термодинамические свойства газа зависят от средней скорости движения атомов или молекул, из которых он состоит.
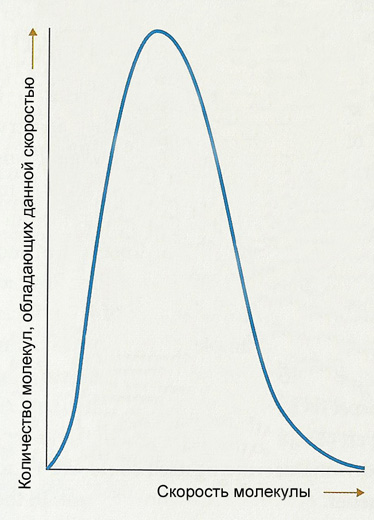
Во второй половине XIX века столь простая внешне картина атомно-молекулярной структуры газов усилиями ряда физиков-теоретиков развилась в мощную и достаточно универсальную теорию. В основу новой теории легла идея о связи измеримых макроскопических показателей состояния газа (температуры, давления и объема) с микроскопическими характеристиками — числом, массой и скоростью движения молекул. Поскольку молекулы постоянно находятся в движении и, как следствие, обладают кинетической энергией, эта теория и получила название молекулярно-кинетической теории газов. Возьмем, к примеру, давление. В любой момент времени молекулы ударяются о стенки сосуда и при каждом ударе передают им определенный импульс силы, который сам по себе крайне мал, однако суммарное воздействие миллионов молекул производит к значительному силовому воздействию на стенки, которое и воспринимается нами как давление. Например, накачивая автомобильное колесо, вы перегоняете молекулы атмосферного воздуха внутрь замкнутого объема шины дополнительно к числу молекул, уже находящихся внутри нее; в результате концентрация молекул внутри шины оказывается выше, чем снаружи, они чаще ударяются о стенки, давление внутри шины оказывается выше атмосферного, и шина становится накачанной и упругой. Смысл теории состоит в том, что по среднему свободному пути молекул мы можем рассчитать частоту их столкновений со стенками сосуда. То есть, располагая информацией о скорости движения молекул, можно рассчитать характеристики газа, поддающиеся непосредственному измерению. Иными словами, молекулярно-кинетическая теория дает нам прямую связь между миром молекул и атомов и осязаемым макромиром. То же самое касается и понимания температуры в рамках этой теории. Чем выше температура, тем больше средняя скорость молекул газа. Эта взаимосвязь описывается следующим уравнением: где Молекулярно-кинетическая теория также дает достаточно определенный ответ на вопрос об отклонениях скоростей отдельных молекул от среднего значения. Каждое столкновение между молекулами газа приводит к перераспределению энергии между ними: слишком быстрые молекулы замедляются, слишком медленные — ускоряются, что и приводит к усреднению. В любой момент в газе происходят несчетные миллионы таких столкновений. Тем не менее выяснилось, что при заданной температуре газа, находящегося в стабильном состоянии, среднее число молекул, обладающих определенной скоростью Эта идея усредненного распределения молекул по скоростям и ее строгая формулировка принадлежит Джеймсу Кларку Максвеллу — этому же выдающемуся теоретику принадлежит и строгое описание электромагнитных полей. Именно он вывел распределение молекул по скоростям при заданной температуре (см. рисунок). Больше всего молекул пребывают в энергетическом состоянии, соответствующем пику распределения Максвелла и средней скорости, однако, фактически, скорости молекул варьируются в достаточно больших пределах. Первое начало термодинамики Теплота представляет собой особую форму энергии и должна учитываться в законе сохранения и превращения энергии. В физике работой называется перемещение массы на определенное расстояние под воздействием силы. Чтобы поднять эту книгу, например, вам нужно приложить силу, направленную вверх, чтобы преодолеть направленную вниз силу гравитационного притяжения на всём отрезке пути, на который вы поднимаете книгу, и тем самым вы совершаете работу. Для совершения работы тело, которое ее совершает, должно обладать запасом энергии, необходимым для совершения этой работы. То есть энергия — это способность совершить работу. С научной точки зрения энергия обладает тремя важнейшими свойствами: во-первых, она может проявляться в различных формах; во-вторых, различные виды энергии могут переходить друг в друга; в-третьих, при любых физических процессах совокупная энергия в замкнутой системе сохраняется. Энергия движения Движущееся тело способно оказывать силовое воздействие на другие тела на отрезке своего пути, и вы такие явления, бесспорно, наблюдали. Представьте себе стрелу, летящую к мишени. Врезаясь в мишень, стрела оказывает силовое воздействие на ее волокна и раздвигает их. Следовательно, движущееся тело способно совершить работу, и значит, по определению, оно обладает энергией. Энергия движения такого рода называется кинетической энергией (от греческого kinezis — «движение»). Согласно механической теории теплоты, теплота — это проявление движения молекул вещества, и значит, ее можно считать особым видом кинетической энергии. Энергия положения Если вы поднимете эту книгу вверх, она сможет затем совершать работу уже в силу своего нового положения в гравитационном поле Земли. Чтобы убедиться в этом, отпустите книгу — и она упадет. Падая, книга разгонится до определенной скорости и, следовательно, приобретет некоторую кинетическую энергию. Упав на пол или на стол, она окажет силовое воздействие на поверхность и едва заметно деформирует ее, одновременно слегка деформировавшись и сама. То есть, находясь на изначальной высоте, книга уже обладала определенным запасом энергии — мы называем ее потенциальной энергией. Будучи поднятой на определенную высоту, книга не совершает никакой работы, однако имеет возможность ее совершить — если книгу уронят. Если быть точным, энергию книги надо назвать потенциальной энергией гравитационного поля, поскольку книга обладает этой энергией благодаря тому, что она находится в гравитационном поле. Именно поле реально производит работу при падении книги. Если вы поднимете книгу в космическом корабле, находящемся в межзвездном пространстве, где нет гравитационного поля, она вообще не упадет, поскольку не будет обладать потенциальной энергией гравитационного поля*. И резинка рогатки, и тетива лука, будучи натянутыми, приобретают потенциальную энергию силы упругости, которая может совершать работу, если их отпустить. Точно так же электрически заряженная частица, помещенная в электрическое поле, обладает электрической потенциальной энергией. Мы видим это в атоме: энергия электрона зависит от удаленности его орбиты от положительно заряженного ядра. Электрическая потенциальная энергия особого рода участвует в химических взаимодействиях между атомами. Электроны в каждом атоме обладают определенной электрической потенциальной энергией, зависящей от их места в атоме. После объединения атомов в молекулы эти же электроны будут обладать уже другой энергией, обусловленной их новым положением. Обычно суммарная энергия до и после химического взаимодействия не одинакова. Энергию, обеспечивающую возможность такого изменения электронной конфигурации атомов, мы называем химической потенциальной энергией. Имеется множество видов потенциальной энергии, связанных с магнитными и электрическими полями, с различными свойствами веществ и т. д. Потенциальная энергия присутствует в любой системе, где может быть совершена работа, которая до сих пор не совершена. Энергия массы В рамках теории относительности Альберт Эйнштейн открыл совершенно неожиданную для всех форму энергии. Оказывается, масса может преобразовываться в энергию, и это получило отражение в формуле Превращение и сохранение энергии Различные виды энергии взаимозаменяемы — энергия может переходить из одного вида в другой. Например, когда лучник выпускает стрелу, потенциальная энергия упругого натяжения тетивы преобразуется в кинетическую энергию летящей стрелы, а при попадании стрелы в мишень — в тепловую энергию рассеяния. Все виды энергии, за исключением тепловой, могут полностью преобразовываться друг в друга (тепловая энергия, согласно второму началу термодинамики, может преобразовываться в работу лишь частично). Преобразование одного вида энергии в другой носит отнюдь не случайный характер, поскольку в замкнутых системах выполняется закон сохранения энергии. Это значит, что в замкнутой изолированной системе совокупное количество энергии со временем не меняется, хотя энергия может принимать различную форму. Предположим, вы располагаете фиксированной суммой денежных средств, распределенных по различным банковским счетам и депозитам: часть ваших денег хранится на текущем сберегательном счете, часть вложена в акции и облигации и т. д. С вашими деньгами вы можете поступить по-разному: можно их все перечислить на единственный счет, можно распределить их по всем счетам равномерно или же положить на разные счета разное количество денег. Однако, что бы вы ни делали, ваш совокупный капитал останется неизменным. (Для простоты мы не учитываем начисление процентов по вкладам и ценным бумагам.) Точно так же, принимая различные формы и перераспределяясь, энергия ниоткуда не поступает и никуда не исчезает. В этом и заключается закон сохранения энергии, который гласит: полная энергия замкнутой системы остается постоянной. * На первый взгляд, это противоречит нашим интуитивным представлениям. Объяснение же таково. В открытом космосе, где нет значительных гравитационных полей, потенциальная энергия, очевидно, должна быть равна нулю. Поскольку при падении тела в направлении звезды или планеты потенциальная энергия теряется, ее значение должно стать отрицательным. Потенциальная энергия книги массой 1 кг в гравитационном поле у поверхности Земли составит около –6 x 107 джоулей, а если книгу поднять на высоту 1000 км, ее потенциальная энергия возрастет до –5 x 107 джоулей. Второе начало термодинамики Невозможна самопроизвольная передача теплоты от холодного тела к теплому. (1) Никакой двигатель не может преобразовывать теплоту в работу со стопроцентной эффективностью. (2) В замкнутой системе энтропия не может убывать. (3) Природным процессам свойственна направленность и необратимость, однако в большинстве законов, описанных в этой книге, это не находит отражения — по крайней мере, явного. Разбить яйца и сделать яичницу не сложно, воссоздать же сырые яйца из готовой яичницы — невозможно. Запах из открытого флакона духов наполняет комнату — однако обратно во флакон его не соберешь. И причина такой необратимости процессов, происходящих во Вселенной, кроется во втором начале термодинамики, который, при всей его кажущейся простоте, является одним из самых трудных и часто неверно понимаемых законов классической физики. Прежде всего, у этого закона имеется как минимум три равноправные формулировки, предложенные в разные годы физиками разных поколений. Может показаться, что между ними нет ничего общего, однако все они логически эквивалентны между собой. Из любой формулировки второго начала математически выводятся две другие. Начнем с первой формулировки, принадлежащей немецкому физику Рудольфу Клаузиусу. Вот простая и наглядная иллюстрация этой формулировки: берем из холодильника кубик льда и кладем его в раковину. По прошествии некоторого времени кубик льда растает, потому что теплота от более теплого тела (воздуха) передастся более холодному (кубику льда). С точки зрения закона сохранения энергии, нет причин для того, чтобы тепловая энергия передавалась именно в таком направлении: даже если бы лед становился всё холоднее, а воздух всё теплее, закон сохранения энергии всё равно бы выполнялся. Тот факт, что этого не происходит, как раз и свидетельствует об уже упоминавшейся направленности физических процессов. Почему именно так взаимодействуют лед и воздух, мы можем легко объяснить, рассматривая это взаимодействие на молекулярном уровне. Из молекулярно-кинетической теории мы знаем, что температура отражает скорость движения молекул тела — чем быстрее они движутся,тем выше температура тела. Значит, молекулы воздуха движутся быстрее молекул воды в кубике льда. При соударении молекулы воздуха с молекулой воды на поверхности льда, как подсказывает нам опыт, быстрые молекулы, в среднем, замедляются, а медленные ускоряются. Таким образом, молекулы воды начинают двигаться всё быстрее, или, что то же самое, температура льда повышается. Именно это мы имеем в виду, когда говорим, что тепло передается от воздуха ко льду. И в рамках этой модели первая формулировка второго начала термодинамики логически вытекает из поведения молекул. При перемещении какого-либо тела на какое-либо расстояние под действием определенной силы совершается работа, и различные формы энергии как раз и выражают способность системы произвести определенную работу. Поскольку теплота, отражающая кинетическую энергию молекул, представляет собой одну из форм энергии, она тоже может быть преобразована в работу. Но опять мы имеем дело с направленным процессом. Перевести работу в теплоту можно со стопроцентной эффективностью — вы делаете это каждый раз, когда нажимаете на педаль тормоза в своем автомобиле: вся кинетическая энергия движения вашего автомобиля плюс затраченная вами энергия силы нажатия на педаль через работу вашей ноги и гидравлической системы тормозов полностью превращается в теплоту, выделяющуюся в процессе трения колодок о тормозные диски. Вторая формулировка второго начала термодинамики утверждает, что обратный процесс невозможен. Сколько ни пытайтесь всю тепловую энергию превратить в работу — тепловые потери в окружающую среду неизбежны. Проиллюстрировать вторую формулировку в действии несложно. Представьте себе цилиндр двигателя внутреннего сгорания вашего автомобиля. В него впрыскивается высокооктановая топливная смесь, которая сжимается поршнем до высокого давления, после чего она воспламеняется в малом зазоре между головкой блока цилиндров и плотно пригнанным к стенкам цилиндра свободно ходящим поршнем. При взрывном сгорании смеси выделяется значительное количество теплоты в виде раскаленных и расширяющихся продуктов сгорания, давление которых толкает поршень вниз. В идеальном мире мы могли бы достичь КПД использования выделившейся тепловой энергии на уровне 100%, полностью переведя ее в механическую работу поршня. В реальном мире никто и никогда не соберет такого идеального двигателя по двум причинам. Во-первых, стенки цилиндра неизбежно нагреваются в результате горения рабочей смеси, часть теплоты теряется вхолостую и отводится через систему охлаждения в окружающую среду. Во-вторых, часть работы неизбежно уходит на преодоление силы трения, в результате чего, опять же, нагреваются стенки цилиндров — еще одна тепловая потеря (даже при самом хорошем моторном масле). В-третьих, цилиндру нужно вернуться к исходной точке сжатия, а это также работа по преодолению трения с выделением теплоты, затраченная вхолостую. В итоге мы имеем то, что имеем, а именно: самые совершенные тепловые двигатели работают с КПД не более 50%. Цикл и теорема Карно 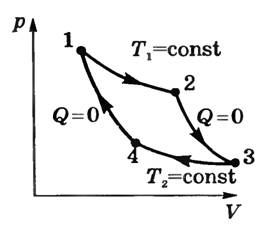 Идеальных машин в реальной жизни не существует, это всего лишь мысленный конструкт. Каждая из таких гипотетических машин, среди которых двигатель Карно занимает немаловажное место, иллюстрирует какое-нибудь важное теоретическое заключение. Двигатель Карно, лежащий в основе работы идеального теплового двигателя, был придуман французским инженером Сади Карно за двадцать лет до того, как были сформулированы основы термодинамики, однако он иллюстрирует важное следствие из второго начала термодинамики. Идеальных машин в реальной жизни не существует, это всего лишь мысленный конструкт. Каждая из таких гипотетических машин, среди которых двигатель Карно занимает немаловажное место, иллюстрирует какое-нибудь важное теоретическое заключение. Двигатель Карно, лежащий в основе работы идеального теплового двигателя, был придуман французским инженером Сади Карно за двадцать лет до того, как были сформулированы основы термодинамики, однако он иллюстрирует важное следствие из второго начала термодинамики.Рабочую часть двигателя Карно можно представить себе в виде поршня в заполненном газом цилиндре. Поскольку двигатель Карно — машина чисто теоретическая, то есть идеальная, силы трения между поршнем и цилиндром и тепловые потери считаются равными нулю. Поршень может свободно перемещаться между двумя тепловыми резервуарами — с высокой температурой и с низкой температурой. (Для удобства представим, что горячий тепловой резервуар нагревается посредством сжигания смеси бензина с воздухом, а холодный — остужается водой или воздухом комнатной температуры.) В этой тепловой машине происходит следующий идеальный четырехфазный цикл:
Двигатель Карно имеет много общего с реальными двигателями: он работает по замкнутому циклу (который называется, соответственно, циклом Карно); он получает энергию извне благодаря высокотемпературному процессу (например, при сжигании топлива); часть энергии рассеивается в окружающую среду. При этом производится определенная работа (в случае двигателя Карно — за счет поступательного движения поршня). КПД, или эффективность двигателя Карно определяется как отношение работы, которую он производит, к энергии (в форме тепла), отнятой у горячего резервуара. Нетрудно доказать, что эффективность где Великое прозрение Карно состоит в том, что он показал, что ни один тепловой двигатель, работающий при двух заданных температурах, не может быть эффективнее идеального двигателя Карно (это утверждение называют теоремой Карно). В противном случае мы столкнулись бы с нарушением второго начала термодинамики, поскольку такой двигатель отбирал бы тепло от менее нагретого резервуара и передавал бы его более нагретому. (На самом деле, второе начало термодинамики является следствием теоремы Карно.) Таким образом, полученное Карно соотношение устанавливает предел эффективности реальных двигателей, работающих в реальном мире. К нему можно приблизиться, но достичь и, тем более превзойти его инженеры не смогут. Так что, чисто гипотетический двигатель Карно играет немаловажную роль в мире реальной, шумной и пахнущей разогретым машинным маслом техники, и это еще один пример прикладного значения чисто теоретических, на первый взгляд, изысканий. Такая трактовка второго начала термодинамики заложена в принципе Карно, который назван так в честь французского военного инженера Сади Карно. Она сформулирована раньше других и оказала огромное влияние на развитие инженерной техники на многие поколения вперед, хотя и носит прикладной характер. Огромное значение она приобретает с точки зрения современной энергетики — важнейшей отрасли любой национальной экономики. Сегодня, сталкиваясь с дефицитом топливных ресурсов, человечество, тем не менее, вынуждено мириться с тем, что КПД, например, ТЭЦ, работающих на угле или мазуте, не превышает 30-35% — то есть, две трети топлива сжигается впустую, точнее расходуется на подогрев атмосферы — и это перед лицом угрозы глобального потепления. Вот почему современные ТЭЦ легко узнать по колоссальным башням-градирням — именно в них остужается вода, охлаждающая турбины электрогенераторов, и избытки тепловой энергии выбрасываются в окружающую среду. И столь низкая эффективность использования ресурсов — не вина, а беда современных инженеров-конструкторов: они и без того выжимают близко к максимуму того, что позволяет цикл Карно. Те же, кто заявляет, что нашел решение, позволяющее резко сократить тепловые потери энергии (например, сконструировал вечный двигатель), утверждают тем самым, что они перехитрили второе начало термодинамики. С тем же успехом они могли бы утверждать, что знают, как сделать так, чтобы кубик льда в раковине не таял при комнатной температуре, а, наоборот, еще больше охлаждался, нагревая при этом воздух. Третья формулировка второго начала термодинамики, приписываемая обычно австрийскому физику Людвигу Больцману, пожалуй, наиболее известна. Энтропия — это показатель неупорядоченности системы. Чем выше энтропия — тем хаотичнее движение материальных частиц, составляющих систему. Больцману удалось разработать формулу для прямого математического описания степени упорядоченности системы. Давайте посмотрим, как она работает, на примере воды. В жидком состоянии вода представляет собой довольно неупорядоченную структуру, поскольку молекулы свободно перемещаются друг относительно друга, и пространственная ориентация у них может быть произвольной. Другое дело лед — в нем молекулы воды упорядочены, будучи включенными в кристаллическую решетку. Формулировка второго начала термодинамики Больцмана, условно говоря, гласит, что лед, растаяв и превратившись в воду (процесс, сопровождающийся снижением степени упорядоченности и повышением энтропии) сам по себе никогда из воды не возродится. И снова мы видим пример необратимого природного физического явления. Тут важно понимать, что речь не идет о том, что в этой формулировке второе начало термодинамики провозглашает, что энтропия не может снижаться нигде и никогда. В конце концов, растопленный лед можно поместить обратно в морозильную камеру и снова заморозить. Смысл в том, что энтропия не может уменьшаться в замкнутых системах — то есть, в системах, не получающих внешней энергетической подпитки. Работающий холодильник не является изолированной замкнутой системой, поскольку он подключен к сети электропитания и получает энергию извне — в конечном счете, от электростанций, ее производящих. В данном случае замкнутой системой будет холодильник, плюс проводка, плюс местная трансформаторная подстанция, плюс единая сеть энергоснабжения, плюс электростанции. И поскольку рост энтропии в результате беспорядочного испарения из градирен электростанции многократно превышает снижение энтропии за счет кристаллизации льда в вашем холодильнике, второе начало термодинамики ни в коей мере не нарушается. А это, я полагаю, приводит еще к одной формулировке второго начала: Холодильник не работает, если он не включен в розетку. Возможно ли нарушение второго начала термодинамики? Демон Максвелла. 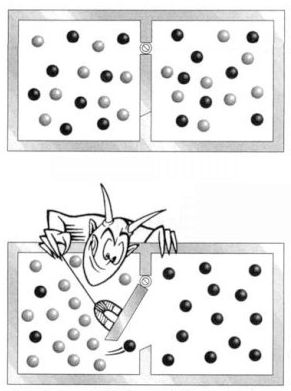 В науке, как и в художественной литературе, встречаются фантастические персонажи. Пожалуй, больше всего их было вымышлено в процессе обсуждения второго начала термодинамики. Самым популярным из них стал демон Максвелла, которого придумал Джеймс Клерк Максвелл, автор знаменитой системы уравнений Максвелла, полностью описывающей электромагнитные поля. Второе начало (или закон) термодинамики имеет множество формулировок, физический смысл которых, однако же, идентичен: изолированная система не может самопроизвольно переходить из менее упорядоченного состояния в более упорядоченное. Так, газ, состоящий из молекул, движущихся с различными скоростями, не может самопроизвольно разделиться на две части, в одной из которых соберутся молекулы, движущиеся, в среднем, быстрее среднестатистической скорости, а в другой — медленнее. В науке, как и в художественной литературе, встречаются фантастические персонажи. Пожалуй, больше всего их было вымышлено в процессе обсуждения второго начала термодинамики. Самым популярным из них стал демон Максвелла, которого придумал Джеймс Клерк Максвелл, автор знаменитой системы уравнений Максвелла, полностью описывающей электромагнитные поля. Второе начало (или закон) термодинамики имеет множество формулировок, физический смысл которых, однако же, идентичен: изолированная система не может самопроизвольно переходить из менее упорядоченного состояния в более упорядоченное. Так, газ, состоящий из молекул, движущихся с различными скоростями, не может самопроизвольно разделиться на две части, в одной из которых соберутся молекулы, движущиеся, в среднем, быстрее среднестатистической скорости, а в другой — медленнее.Многие физические процессы относятся к категории обратимых. Воду, например, можно заморозить, а полученный лед снова растопить, и мы получим воду в прежнем объеме и состоянии; железо можно намагнитить, а затем размагнитить и т. п. При этом энтропия (степень упорядоченности) системы в начальной и конечной точке процесса остается неизменной. Есть и необратимые в термодинамическом понимании процессы — горение, химические реакции и т. п. То есть, согласно второму началу термодинамики, любой процесс в итоге приводит либо к сохранению, либо к снижению степени упорядоченности системы. Такая дисгармоничная ситуация сильно озадачила физиков второй половины XIX столетия, и тогда Максвелл предложил парадоксальное решение, позволяющее, казалось бы, обойти второе начало термодинамики и обратить неуклонный рост хаоса в замкнутой системе. Он предложил следующий «мысленный эксперимент»: представим себе герметичный контейнер, разделенный надвое газонепроницаемой перегородкой, в которой имеется единственная дверца размером с атом газа. В начале опыта в верхней части контейнера содержится газ, а в нижней — полный вакуум. Теперь представим, что к дверце приставлен некий микроскопический вахтер, зорко следящий за молекулами. Быстрым молекулам он дверцу открывает и пропускает их за перегородку, в нижнюю половину контейнера, а медленные оставляет в верхней половине. Понятно, что если такой мини-вахтер будет дежурить у дверцы достаточно долго, газ разделится на две половины: в верхней части останется холодный газ, состоящий из медленных молекул, а в нижней скопится горячий газ из быстрых молекул. Тем самым система упорядочится по сравнению с исходным состоянием, и второе начало термодинамики будет нарушено. Мало того, разницу температур можно будет использовать для получения работы. Если такого вахтера оставить на дежурстве навечно (или организовать сменное дежурство), мы получим вечный двигатель. Этот забавный вахтер, которому остроумные коллеги ученого дали прозвище «демон Максвелла», до сих пор живет в научном фольклоре и волнует умы ученых. Действительно, вечный двигатель человечеству бы не повредил, но вот беда: судя по всему, чтобы демон Максвелла заработал, ему самому потребуется энергопитание в виде притока фотонов, необходимых для освещения приближающихся молекул и их просеивания. Кроме того, просеивая молекулы, демон и дверца не могут не вступать с ними во взаимодействие, в результате чего они сами будут неуклонно получать от них тепловую энергию и наращивать свою энтропию, в результате чего суммарная энтропия системы всё равно уменьшаться не будет. То есть таким объяснением теоретическая угроза второму началу термодинамики была отведена, но не безоговорочно. Первый по-настоящему убедительный контраргумент был сформулирован вскоре после зарождения квантовой механики. Для сортировки подлетающих молекул демону нужно измерять их скорость, а сделать это с достаточной точностью он не может в силу принципа неопределенности Гейзенберга. Кроме того, в силу этого же принципа он не может точно определить и местонахождение молекулы в пространстве, и часть молекул, перед которыми он распахивает микроскопическую дверцу, с этой дверцей разминутся. Иными словами, демон Максвелла на поверку оказывается макроскопическим слоном в посудной лавке микромира, который живет по собственным законам. Приведите демона в соответствие с законами квантовой механики, и он окажется не в состоянии сортировать молекулы газа и просто перестанет представлять какую-либо угрозу второму началу термодинамики. Другой веский аргумент против возможности существования демона-вахтера появился уже в компьютерную эру. Предположим, что демон Максвелла — это компьютерная автоматизированная система управления открыванием дверцы. Система производит побитовую обработку входящей информации о скорости и координатах приближающихся молекул. Пропустив или отклонив молекулу, система должна произвести сброс прежней упорядоченной информации — а это равносильно повышению энтропии на величину, равную снижению энтропии в результате упорядочивания газа при пропускании или отклонении молекулы, информация о которой стерта из оперативной памяти компьютерного демона. Сам компьютер, к тому же, также греется, так что и в такой модели в замкнутой системе, состоящей из газовой камеры и автоматизированной пропускной системы, энтропия не убывает, и второй закон термодинамики выполняется. Жаль демона — симпатичный был персонаж. Третье начало термодинамики Невозможно за конечное время довести температуру тела до абсолютного нуля. Абсолютный ноль — это одна из концепций с интригующим названием и обманчиво простым определением. До наступления эры квантовой механики определение абсолютного нуля действительно было предельно простым. Молекулярно-кинетическая теория выявила статистическую связь между движениями атомов и молекул и температурой, и природу температуры стало возможно представить наглядно: чем быстрее движутся молекулы, тем выше температура, и наоборот. При такой картине нетрудно догадаться, что имеется нижний предел температуры, по достижении которого атомы и молекулы перестают двигаться окончательно. Значение абсолютного нуля оказалось равным –273°C. В рамках квантовой механики значение абсолютного нуля не изменилось, однако в корне изменилось наше представление о том, как ведут себя атомы. Если бы атомы просто остановились как вкопанные, мы бы, в таком случае, могли одновременно измерить их скорость и местоположение с абсолютной точностью, а это — нарушение принципа неопределенности Гейзенберга. Поэтому даже при абсолютном нуле атом должен представляться нам слегка расплывчатым, если использовать волновое представление о нем, или слегка колеблющимся, если использовать корпускулярную концепцию. Поэтому нам следует говорить, что при абсолютном нуле атом не прекращает всякое движение, а лишь приходит в такое колебательное состояние, при котором он более не способен отдавать энергию вовне (такая остаточная энергия атома называется энергией нулевой точки). Конечный же итог, с макроскопической точки зрения, остается неизменным: имеется минимальное значение возможной температуры вещества, и оно равно всё тем же –273°С. На самом деле, существование энергии нулевой точки хорошо иллюстрирует весьма интересный момент в квантовой теории. При стремлении температуры к абсолютному нулю волновая природа материи (см. Уравнение Шрёдингера) становится всё очевиднее и важнее, а квантово-механические эффекты начинают преобладать над эффектами классической механики, при которых атом ведет себя подобно бильярдному шару. Так получилось, что –273°С — единственная температура, фигурирующая в фундаментальных физических законах. Она же используется и в определении температурной шкалы Кельвина, которая в основном используется в точных науках. За ноль в ней принимается абсолютный ноль, а единичное деление шкалы принимается равным 1° по привычной шкале Цельсия. Таким образом, по шкале Кельвина абсолютный ноль равен 0 К, точка замерзания воды приходится на 273 К, а комнатная температура составляет около 300 К. Третье начало термодинамики просто констатирует, что абсолютный ноль недостижим — и в этом он похож на скорость света: материальное тело может сколь угодно близко подойти к нему, но достичь — никогда. Дело в том, что чем ближе система подходит к абсолютному нулю температуры, тем больше работы нужно затратить на ее дальнейшее охлаждение. На самом деле, в лабораторных условиях ученым удавалось получать температуры предельно близкие к нулевой. Сегодня температуры, отстоящие от абсолютного нуля на миллиардные доли градуса, можно получить практически в любой криогенной лаборатории. Способов понижения температуры материального тела имеется достаточно много. Можно испарять жидкость с его поверхности, и она будет отнимать теплоту у тела — именно поэтому люди потеют в жару. Можно резко расширять газ, находившийся под высоким давлением, — вот почему охлаждается аэрозольный баллончик, когда вы долго выпускаете из него содержимое. Подобными методами ученые доводят температуру до уровня нескольких градусов выше абсолютного нуля. Однако чтобы получить по-настоящему сверхнизкие температуры, приходится надолго подвешивать незначительное количество атомов вещества в сильных электростатических и магнитных полях. После этого подвешенные атомы обрабатываются лазерным лучом определенной длины волны, который сначала заставляет атомы испустить остатки энергии возбужденных электронов в виде световых квантов, а затем — разогнать атомы врозь, как бы распрыскать их из аэрозольного баллончика. Именно так сегодня получаются температуры порядка нескольких нанокельвинов (1нК = 10–9 К). Однако, как далеко ни пошло бы развитие нашей техники, третье начало термодинамики говорит нам, что мы не только не перейдем барьера абсолютного нуля, но даже не достигнем его. Один физик с хорошим чувством юмора дал собственные формулировки трех начал термодинамики: Первое начало термодинамики: Вам не выиграть.
Второе начало термодинамики: Вам не сыграть вничью. Третье начало термодинамики: Вам даже сыграть не дадут.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Законы термодинамики |
|
[time: 29 ms; queries: 7]
7 Мар 2026 06:03:09 GMT+3 |


 Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.
Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.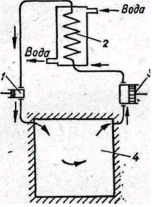 Воздух как хладагент безвреден, общедоступен, безопасен и почти нейтрален к металлам и смазочным маслам, поэтому его применение в холодильной технике весьма удобно. Однако его недостатком является малая объемная холодопроизводительность.
Воздух как хладагент безвреден, общедоступен, безопасен и почти нейтрален к металлам и смазочным маслам, поэтому его применение в холодильной технике весьма удобно. Однако его недостатком является малая объемная холодопроизводительность. Тот факт, что у нас есть одно временное и три пространственных измерений, можно вывести из антропного принципа (мы видим Вселенную такой, какой видим, просто потому что только в такой Вселенной мог возникнуть наблюдатель-человек). Скажем, Пауль Эренфест показал, что для одного временного и больше трех пространственных измерений орбиты планет вокруг звезд будут нестабильны, значит, жизнь в привычном нам виде в такой Вселенной невозможна. Есть похожие результаты для стабильности ядер и прочих физических процессов. Работа мексиканских физиков не претендует на всеохватность предложенного в ней объяснения, но позволяет получить три пространственных и одно временное измерение пользуясь минимумом физических — принципами термодинамики — и некотором количестве естественных математических предположений
Тот факт, что у нас есть одно временное и три пространственных измерений, можно вывести из антропного принципа (мы видим Вселенную такой, какой видим, просто потому что только в такой Вселенной мог возникнуть наблюдатель-человек). Скажем, Пауль Эренфест показал, что для одного временного и больше трех пространственных измерений орбиты планет вокруг звезд будут нестабильны, значит, жизнь в привычном нам виде в такой Вселенной невозможна. Есть похожие результаты для стабильности ядер и прочих физических процессов. Работа мексиканских физиков не претендует на всеохватность предложенного в ней объяснения, но позволяет получить три пространственных и одно временное измерение пользуясь минимумом физических — принципами термодинамики — и некотором количестве естественных математических предположений Если Вселенная бесконечна, однородна и стационарна (а в XVIII-XIX веках астрономы в этом не сомневались), то в небе — в каком направлении ни посмотри — рано или поздно окажется звезда. То есть, всё небо должно быть сплошным образом заполнено яркими светящимися точками звезд. То есть, в ночи небо должно ярко светиться. А мы почему-то наблюдаем сплошное черное небо лишь с отдельными звездами.
Если Вселенная бесконечна, однородна и стационарна (а в XVIII-XIX веках астрономы в этом не сомневались), то в небе — в каком направлении ни посмотри — рано или поздно окажется звезда. То есть, всё небо должно быть сплошным образом заполнено яркими светящимися точками звезд. То есть, в ночи небо должно ярко светиться. А мы почему-то наблюдаем сплошное черное небо лишь с отдельными звездами. Идеальный газ. Уравнение состояния газа. Взаимосвязь давления, температуры и объёма. Механизмы рождения макропараметров в рамках «молекулярного бильярда». Первое начало термодинамики как закон сохранения энергии. Вывод уравнения Бернулли. Энтропия и второе начало термодинамики. Тепловые машины и цикл Карно. Энтропия информационная. Энтропия как неопределённость. Аксиоматический подход к определению энтропии. Принцип максимума энтропии. Подход статистической физики за пределами термодинамики.
Идеальный газ. Уравнение состояния газа. Взаимосвязь давления, температуры и объёма. Механизмы рождения макропараметров в рамках «молекулярного бильярда». Первое начало термодинамики как закон сохранения энергии. Вывод уравнения Бернулли. Энтропия и второе начало термодинамики. Тепловые машины и цикл Карно. Энтропия информационная. Энтропия как неопределённость. Аксиоматический подход к определению энтропии. Принцип максимума энтропии. Подход статистической физики за пределами термодинамики. Эрвин Рудольф Йозеф Александр Шредингер - австрийский физик-теоретик, лауреат Нобелевской премии по физике. Один из разработчиков квантовой механики и волновой теории материи. В 1945 г. Шредингер пишет книгу "Что такое жизнь с точки зрения физики?", оказавшую существенное влияние на развитие биофизики и молекулярной биологии. В этой книге внимательно рассмотрено несколько важнейших проблем. Основополагающим является вопрос: "Как могут физика и химия объяснить те явления в пространстве и времени, которые имеют место внутри живого организма?" Прочтение этой книги даст не только обширный теоретический материал, но и заставит задуматься над тем, что же в сущности есть жизнь?
Эрвин Рудольф Йозеф Александр Шредингер - австрийский физик-теоретик, лауреат Нобелевской премии по физике. Один из разработчиков квантовой механики и волновой теории материи. В 1945 г. Шредингер пишет книгу "Что такое жизнь с точки зрения физики?", оказавшую существенное влияние на развитие биофизики и молекулярной биологии. В этой книге внимательно рассмотрено несколько важнейших проблем. Основополагающим является вопрос: "Как могут физика и химия объяснить те явления в пространстве и времени, которые имеют место внутри живого организма?" Прочтение этой книги даст не только обширный теоретический материал, но и заставит задуматься над тем, что же в сущности есть жизнь?