Глава 10. От Фалеса до Евклида

• 10.1. Доказательство
• 10.2. Классический период
• 10.3. Философия Платона
• 10.4. Что такое математика?
• 10.5. Точность сравнения величин
• 10.6. Достоверность утверждений математики
• 10.7. В поисках аксиом
• 10.8. Об аксиомах арифметики и логики
• 10.9. Сваи, уходящие вглубь
• 10.10. Платонизм в ретроспективе

10.1. Доказательство

Ни в египетских, ни в вавилонских текстах мы не находим ничего, что хотя бы отдаленно было похоже на математическое доказательство. Понятие о доказательстве ввели греки, и это является их величайшей заслугой. Какими-то наводящими соображениями при получении новой формулы люди, очевидно, пользовались и раньше, мы даже приводили пример грубо неверной формулы (для площади неправильных четырехугольников у египтян), явно полученной из внешне правдоподобных «общих соображений». Но только греки стали относиться к этим наводящим соображениям с той серьезностью, которой они заслуживают, стали анализировать эти соображения с точки зрения их убедительности и ввели принцип, согласно которому каждое утверждение, касающееся чисел и фигур (формула), за исключением лишь небольшого числа, должно быть доказано, выведено убедительным, не допускающим сомнений образом из этих «совершенно очевидных» истин. Неудивительно, что именно греки с их демократическим общественным строем создали учение о математическом доказательстве. Споры и доказательство играли важнейшую роль в жизни граждан греческого города-государства (полиса). Понятие о доказательстве уже существовало, оно было общественно значимой реальностью. Осталось только перенести его в область математики, что и было сделано, едва греки познакомились с достижениями древних восточных цивилизаций. Сыграло здесь роль, надо полагать, и то положение молодого любознательного ученика, в котором оказались греки по отношению к египтянам и вавилонянам — своим старшим и не всегда согласным друг с другом учителям. В самом деле, вавилоняне определяют площадь круга по формуле 3r², а египтяне по формуле (⁸/₉ 2r)² . Где же истина? Здесь есть о чем подумать и поспорить.

Творцы египетской и вавилонской математики остались безымянными. Греки сохранили имена своих мудрецов. Первое из них — имя Фалеса Милетского — является также первым именем, вошедшим в историю науки. Фалес жил в VI в. до н. э. в городе Милете на Малоазиатском побережье Эгейского моря. Одна дата из его жизни установлена твердо: в 585 г. до н. э. он предсказал солнечное затмение. Этот факт, кстати, неоспоримо свидетельствует о знакомстве Фалеса с культурой древних цивилизаций, ибо, чтобы установить периодичность затмений, необходим опыт десятков и сотен лет. Так как у Фалеса не было греческих предшественников, он мог заимствовать свои познания по астрономии только у ученых Востока.

Рис. 10.1. Равнобедренный треугольник

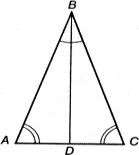
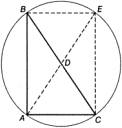
Фалес, как утверждают греки, дал миру первые математические доказательства. В числе доказанных им положений (теорем) называют следующие:

Диаметр делит круг на две равные части.

Углы при основании равнобедренного треугольника равны.

Два треугольника, у которых одинаковы стороны и прилежащие к ней углы, равны.

Кроме того, он первый дал построение круга, описанного вокруг прямоугольного треугольника (и в честь этого открытия, как говорят, принес в жертву быка).

Простейший характер указанных теорем, их интуитивная очевидность показывают, что Фалес полностью осознавал значение доказательства как такового. Эти теоремы, явно доказывались не потому, что были сомнения в их истинности, а с целью положить начало систематическому нахождению доказательств, разработать технику доказательства. Имея такую цель, естественно начинать с доказательства самых простых предложений.

Пусть треугольник ABC равнобедренный (рис. 10.1), т. е. сторона AB равна стороне BC. Разделим угол ABC линией BD на две равные части. Перегнем мысленно наш чертеж по линии BD. Так как угол ABD равен CBD, линия BA ляжет на линию BC, а так как длины отрезков AB и BC равны, точка A ляжет на точку C. Поскольку точка D остается на месте, углы BCD и BAD должны быть равны. Если раньше нам только казалось, что углы BCD и BAD одинаковы (так, вероятно, говорил своим согражданам Фалес), то теперь мы доказали, что эти углы необходимо и с абсолютной точностью должны быть равны (тогда говорили «подобны») друг другу, т. е. совмещаться при наложении.

Рис. 10.2. Построение окружности, описанной вокруг прямоугольного треугольника

Теперь сделаем решающий шаг. Дополним треугольник точкой E до прямоугольника ABEC и проведем в нем вторую диагональ AE. И внезапно становится очевидной равнобедренность треугольника ADC. Действительно, из общей симметрии чертежа ясно, что диагонали равны и пересекаются в точке, которая делит их пополам, т. е. в точке D. Это еще не доказательство, но уже тот уровень ясности, когда формальное завершение доказательства не представляет труда. Например, опираясь на равенство противолежащих сторон прямоугольника (которое при желании можно вывести из еще более очевидных положений), мы завершим доказательство следующим рассуждением: треугольники ABC и AEC равны, так как сторона AC у них общая, стороны AB и ЕС равны, а углы BAC и ЕСА прямые; следовательно, угол ЕАС равен углу BCA, т. е. треугольник ADC равнобедренный, что и требовалось доказать.

10.2. Классический период

Итак, несколько дополнительных точек и линий на чертеже, цепочка логических рассуждений — и в результате из простых и очевидных истин мы получаем истины далеко не простые и далеко не очевидные, в справедливости которых, однако, никто не может ни на минуту усомниться. Это стоит того, чтобы принести в жертву богам быка! Можно представить себе восторг, который испытали греки, совершив такое открытие. Они напали на золотую жилу и с усердием принялись ее разрабатывать. Уже во времена Пифагора (550 г. до н. э.) занятия математикой были очень распространены среди людей, обладавших досугом, и считались делом благородным, почетным и даже священным. Достижения и открытия, одно другого чудеснее, посыпались как из рога изобилия.

Возникновение доказательства — это метасистемный переход в рамках языка. Формула перестает быть вершиной языковой деятельности, появляется новый класс языковых объектов — доказательства и новый вид языковой деятельности, направленный на исследование и производство формул. Это новый этаж иерархии по управлению, и его появление вызывает огромный рост числа формул (закон разрастания предпоследнего уровня).

Метасистемный переход всегда означает качественный скачок, взлет на новую ступень, бурное взрывоподобное развитие. Математика стран Древнего Востока оставалась почти неизменной на протяжении одного-двух тысячелетий, и наш современник читает о ней со снисхождением взрослого к ребенку. Греки же за одно-два столетия создали всю геометрию, над изучением которой трудятся в поте лица наши старшеклассники. И даже больше, ибо школьная программа по геометрии охватывает лишь часть достижений культуры (до 330 г. до н. э.). Вот краткая летопись математики классического периода.

585 г. до н. э. Фалес Милетский. Первые геометрические теоремы.

550 г. до н. э. Пифагор и его последователи. Теория чисел. Учение о гармонии. Построение правильных многогранников. Теорема Пифагора. Открытие несоизмеримых отрезков. Геометрическая алгебра. Геометрические построения, эквивалентные решению квадратных уравнений.

500 г. до н. э. Гиппас-пифагореец, который должен был порвать со своими товарищами, так как делился с посторонними людьми своими знаниями и открытиями (у пифагорейцев это запрещалось). Он дал, в частности, построение шара, описанного вокруг додекаэдра.

430 г. до н. э. Гиппократ Хиосский (не путать с врачом Гиппократом из Коса). Считался самым знаменитым геометром V в. до н. э. Занимался квадратурой круга, осуществляя сложные геометрические построения. Ему известна связь между вписанными углами и дугами, построение правильного шестиугольника, обобщение теоремы Пифагора для тупоугольных и остроугольных треугольников. Все это для него, видимо, уже азбучные истины. Он может квадрировать любой многоугольник, т. е. построить для него квадрат равной площади.

427–348гг. до н. э. Платон. Он сам хотя и не получал новых математических результатов, но математику знал, и она играла важную роль в его философии точно так же, как философия Платона сыграла важную роль в математике. Крупнейшие математики своего времени: Архит, Теэтет, Евдокс и другие были друзьями Платона, его учениками в области философии и учителями в области математики.

390 г. до н. э. Архит Тарентский. Стереометрическое решение задачи об удвоении куба, т. е. построение куба с объемом, равным удвоенному объему данного куба.

370 г. до н. э. Евдокс Книдский. Изящная, логически безукоризненная теория пропорций, вплотную подходящая к современной теории действительного числа. «Метод исчерпывания», лежащий в основе современного понятия об интеграле.

384–322 гг. до н. э. Аристотель. Он положил начало логике и физике. Труды Аристотеля обнаруживают полное владение математическим методом и знание математики, хотя он, подобно своему учителю Платону, и не сделал в ней никаких открытий. Аристотель-философ немыслим без Аристотеля-математика.

300 г. до н. э. Евклид. Он живет уже в новую Александрийскую эпоху. В своих знаменитых «Началах» Евклид собрал и систематизировал все важнейшие труды по математике, существовавшие в конце IV в. до н. э., и изложил их в том же духе, как это было принято в школе Платона. В течение более чем двух тысячелетий школьные курсы геометрии следуют, с большей или меньшей степенью точности, «Началам» Евклида.

10.3. Философия Платона

Что такое математика? О чем эта наука? Эти вопросы стали задавать греки, начав сооружать основанное на доказательствах здание математики, ибо ореол абсолютной достоверности, чуть ли не священности математического знания, который оно приобрело благодаря наличию доказательств, сразу же выделил его на фоне остальных, обыденных, житейских познаний. Ответ был дан платоновской теорией идей. Эта теория легла в основу всей греческой философии, определила стиль и образ мышления образованных греков и оказала огромное влияние на дальнейшее развитие философии и науки греко-римско-европейской культуры. Логику, которая привела Платона к его теории, установить нетрудно. О чем идет речь в математике? О точках, линиях, прямоугольных треугольниках и т. д. Но существуют ли в природе точки, не имеющие размеров. Или абсолютно прямые и бесконечно тонкие линии? Или в точности равные отрезки, углы, площади? Ясно, что нет. Выходит, что математика изучает несуществующие, воображаемые вещи, что это наука ни о чем. Но согласиться с этим было бы никак невозможно. Во-первых, математика приносила неоспоримую практическую пользу. Правда, Платон и его последователи относились к практике с презрением, но это было уже логическим следствием философии, а не ее посылкой. Во-вторых, всякий человек, изучающий математику, совершенно ясно чувствует, что имеет дело с реальностью, а не с фикцией, и никакими логическими доводами искоренить это ощущение невозможно. Следовательно, объекты математики реально существуют, но не как материальные предметы, а как образы, или идеи, потому что слово идея (ίδєα) по-гречески и означало образ, вид¹. Идея существует вне мира материальных вещей и независимо от него. Чувственно воспринимаемые материальные вещи суть лишь несовершенные и временные копии (или тени) совершенных и вечных идей. Утверждение о реальном, объективном существовании мира идей и составляет сущность учения Платона («платонизма»).

Попытки как-то конкретизировать представления о мире идей и его взаимодействии с материальным миром вызывали в среде платоников (на протяжении многих столетий) безнадежно неразрешимые споры. Сам Платон умудрился остаться неуязвимым, избегая конкретизации и пользуясь языком метафорическим и поэтическим. Впрочем, уже ему пришлось вступить в полемику со своим учеником Евдоксом, который не только доказывал математические теоремы, но еще и отстаивал утверждение, что идеи «примешиваются» к чувственно воспринимаемым вещам, обусловливая их свойства.

Понятия математики не являются единственными обитателями «мира идей» Платона. Всякое общее понятие претендует на место в этом мире. Рассуждение, обосновывающее эту претензию, таково. В нашем языке существуют слова и словосочетания для обозначения единичных понятий, например имена собственные: остров Самос, Афины, Гиппократ. Откуда у нас возникают эти понятия? Из чувственного восприятия соответствующих вещей. Но есть у нас и общие понятия: человек, дерево и т. п. Откуда же у нас берутся эти понятия? Ведь путем чувственного восприятия мы постигаем только конкретные понятия: данный человек, данное дерево и т. д. Если вещи порождают у нас конкретные понятия, то что же порождает общие понятия? Ответ Платона гласит: идеи; идея человека, идея дерева и т. д.

Существование мира идей обеспечивает математике прочное и высокое положение — она становится наукой об идеях. Чувственный опыт дает нам несовершенное, приблизительное знание о несовершенных, приблизительных воплощениях идей. Доказательства математики дают совершенное знание о самих идеях. «При помощи математики, — пишет Платон, — очищается и получает новую жизненную силу орган души, в то время как другие занятия уничтожают его и лишают способности видеть, тогда как он значительно более ценен, чем тысяча глаз, ибо только им одним может быть обнаружена истина».

Под влиянием идеализма Платона математики древней Греции стремились изгнать из своей науки все, что можно истолковать как обращение к данным чувственного опыта. С одной стороны, это имело положительные последствия, так как способствовало разработке техники доказательства и привело к созданию понятия о дедуктивной теории. Греки старались сделать доказательства логически безукоризненными, исключить из них сомнительные выводы и неявные допущения, апеллирующие к наглядности. Они доказывали, а не показывали. Число явных допущений они стремились свести к минимуму, оставить из них лишь те, которые можно было считать выражением свойств «самих идей», а не вещей, т. е. свойств, открывающихся разуму, «внутреннему взору», а не органам чувств. Эти допущения включались в определения исходных понятий или, точнее, слов, ибо понятия (идеи) существовали для греков как объективная реальность, независимая от всяких слов, а определения нужны были лишь для того, чтобы не ошибиться в установлении соответствия между словами и понятиями. Так что явные допущения, делаемые греческими математиками, представлялись им не определениями в современном смысле слова (согласно которому определение порождает математический объект), а просто указаниями на те из истинных свойств реально существующих идей, которые постигаются разумом легче, чем другие, — без вспомогательных рассуждений. Если исключить это отличие и вытекающие из него вольности в обращении с элементарнейшими свойствами геометрических фигур, то в остальном греческая математика удовлетворяет самым высоким современным стандартам; в соотношении логической обоснованности понятий и строгости вывода она несравненно выше, чем европейская математика до середины XIX в. С другой стороны, образ мышления, выраженный в философии Платона, имел и отрицательное влияние. Прежде всего, он приводил к определенному «чистоплюйству» греческих ученых, нежеланию заниматься проблемами, имеющими прикладное, практическое значение. Это пренебрежение распространялось даже на приближенные вычисления. «Приближенными вычислениями стыдно заниматься свободному человеку, они — удел раба», — говорилось в то время. Действительно, приближенные вычисления не приводят к истинным соотношениям, а значит, и не имеют никакого отношения к миру идей; это занятие того же рода, как возделывание масличных деревьев или торговля оливковым маслом. Такая позиция, конечно, ограничивала приток новых задач и идей, способствовала канонизации и регламентации научной мысли, сдерживая тем самым ее развитие. Но, сверх этого, платонизм имел и более конкретное отрицательное влияние на математику, помешав грекам создать алгебраический язык. Это смогли сделать только менее вышколенные и более практичные европейцы. Ниже мы более подробно рассмотрим историю создания современного алгебраического языка и тормозящую роль платонизма, но сначала поговорим об ответах, которые дает современная наука на вопросы, поставленные в платоновское время, и о том, как выглядят ответы, данные Платоном, в исторической ретроспективе.

10.4. Что такое математика?

Для нас математика — это прежде всего язык, позволяющий создавать определенного рода модели действительности — математические модели. Как и в любом другом языке (или ответвлении языка), языковые объекты математики — математические объекты — суть материальные предметы, фиксирующие определенные функциональные единицы — математические понятия. Когда мы говорим, что объекты «фиксируют функциональные единицы», мы понимаем под этим, что человек, используя распознающие способности своего мозга, совершает над этими объектами или в связи с ними определенную языковую деятельность. Ясно, что не конкретный вид (форма, вес, запах) математического объекта играет роль в математике, а именно языковая деятельность, с ним связанная. Поэтому термины «математический объект» и «математическое понятие» часто употребляют как синонимы. Языковая деятельность в математике естественным образом распадается на две части: установление связи между математическими объектами и неязыковой реальностью (эта деятельность определяет семантику математических понятий) и преобразования внутри языка — математические выкладки и доказательства. Математической деятельностью обычно называют только вторую часть, а первую называют приложением математики.

Точки, линии, прямоугольные треугольники и прочее — все это математические объекты, это предметы, которые образуют наши геометрические чертежи или стереометрические модели: пятна краски, шарики из пластилина, проволочки, куски картона и т. п. Семантика этих объектов известна: точка, например, это объект, размерами и формой которого можно пренебречь. Таким образом, «точка» — это просто абстрактное понятие, характеризующее отношение объекта к его окружению. В некоторых случаях мы всю нашу планету рассматриваем как точку. Но когда мы строим математическую (геометрическую) модель, мы обычно наносим на бумагу маленькое пятнышко краски и говорим: «пусть дана точка A». Это пятнышко краски и есть языковый объект L_i, а планета Земля может оказаться в роли соответствующего объекта R_i. Никаких других, «настоящих» или «идеальных», т. е. не имеющих размеров, точек нет. Часто говорят, что «настоящих» точек нет в природе, но они существуют в нашем воображении. Это ходячее высказывание либо абсолютно бессмысленно, либо ложно — в зависимости от того, как его толковать. В любом случае оно приносит вред, так как затемняет суть дела. Никаких «настоящих» точек в нашем воображении нет и быть не может. Когда мы говорим, что представляем себе точку, мы просто представляем очень маленький предмет. Можно вообразить только то, что можно составить из данных чувственного опыта. Да и то далеко не все. Число тысяча, например, вообразить нельзя. И большие числа, и идеальные точки, и линии существуют не в нашем воображении, а в нашем языке — как языковые объекты, с которыми мы обращаемся определенным образом. В этих правилах обращения и проявляется сущность математических понятий, в частности «настояшесть» точки: размеры точек на чертеже не влияют на ход доказательства, а если надо поставить две точки так близко, что они сольются в одну, мы можем увеличить масштаб.

Но разве не свойственна утверждениям математики абсолютная точность и достоверность, резко отличающая их от содержания эмпирического знания, по преимуществу приблизительного и гипотетического? Путем измерения мы можем обнаружить, что два отрезка примерно равны, но никогда, что они равны в точности; такие утверждения — привилегия математики. На основании многовекового опыта человечества мы каждый вечер после захода Солнца можем предсказать, что завтра рано утром оно взойдет вновь. Но это предсказание — всего лишь гипотеза, хотя и весьма вероятная. Не исключена возможность, что где-то в недрах Солнца или вне его назревает космическая катастрофа неизвестной природы, в результате которой Солнце погаснет или развалится на части. Когда же мы говорим, что если к двум прибавить два, то будет четыре, или что уравнение x² = 2 не имеет рациональных решений, мы убеждены, что эти предсказания абсолютно достоверны и будут верны всегда и всюду, если даже не только Солнце, но и вся Галактика развалится на кусочки. Мы просто не можем представить себе, чтобы было иначе. Существует, следовательно, различие между математическими моделями действительности и другими моделями, составляющими содержание нашего житейского опыта и естественных наук. Какова же природа этого различия?

10.5. Точность сравнения величин

Легко видеть, что абсолютная точность сравнения измеримых объектов в математике и абсолютная однозначность математических утверждений являются просто следствием того, что язык математики представляет собой дискретную кибернетическую систему. В самом ли деле дискретную? По отношению к арифметике, алгебре и вообще к языку символов это не вызывает сомнения. Если головку у двойки увеличить или уменьшить, от этого она не превратится ни 2,01, ни в 1,99. Текст из N символов — это кибернетическая система из N подсистем, каждую из которых можно представлять себе в виде клеточки, содержащей символ; пусть полное число различных символов есть n, тогда каждая подсистема может находиться в одном из n состояний. Но геометрический язык — язык фигур — на первый взгляд представляется непрерывной системой. Линии на чертеже могут иметь произвольную длину, образовывать произвольные углы и т. д. И все же в действии геометрический язык оказывается дискретной системой. Детали геометрического чертежа такие, как значения длины отрезков и величин углов, не играют роли ни для хода доказательства, ни для декодирования чертежа. Существенны лишь такие особенности чертежа, как: пересекаются ли две данные прямые, проходит ли данная прямая через данную точку, лежит ли данная точка на пересечении данной прямой и данной окружности и т. п. Всю эту информацию можно закодировать текстом с помощью какой-либо специальной системы обозначений или просто на русском языке. Язык геометрии можно сравнить с языком игры в шахматы. Шахматные фигуры никогда не занимают строго центральное положение в квадратах шахматной доски, могут даже отчасти вылезать за пределы своего квадрата, но это никак не влияет на ходы, которые можно делать фигурами.

Утверждения об абсолютно точном равенстве отрезков, углов и т. п. это просто некоторые состояния системы «геометрический язык». Так как эта система дискретна и детерминированна — при условии соблюдения правил логического вывода, то, если из условий задачи следует, что AB = BC, мы неизменно будем получать этот результат, сколько бы раз ни повторяли доказательство (предполагается, конечно, что система аксиом не противоречива — только такие системы имеют право на существование в математике). Поскольку условие задачи уже формулируется на геометрическом языке, весь путь от условия к результату есть синтаксическое преобразование L₁ → L₂ внутри дискретной языковой системы. Совсем другой статус имеют утверждения эмпирического языка. Сам по себе этот язык, конечно, тоже дискретен, но эмпирические утверждения отражают семантические преобразования L₁ → S₁ выводящие нас в область неязыковой действительности, которая не является ни дискретной, ни детерминированной. Когда мы говорим, что два стержня имеют равную длину, это означает, что процесс их измерения будет всякий раз давать одинаковый результат. Однако из опыта известно, что, имея возможность неограниченно повышать точность измерения, мы рано или поздно обязательно получим разнящиеся значения длины, поэтому эмпирическое утверждение об абсолютно точном равенстве вообще лишено смысла. Другие утверждения эмпирического языка, которые имеют смысл и могут быть выражены на языке исчисления предикатов, например «стержень номер 1 меньше, чем стержень номер 2», обладают той же «абсолютной точностью», являющейся тривиальным следствием дискретности языка, что и математические утверждения о равенстве отрезков: это утверждение либо «в точности» истинно, либо «в точности» ложно. Однако из-за вариаций процесса измерения ни то, ни другое не является абсолютно достоверным.

10.6. Достоверность утверждений математики

Теперь о достоверности математических утверждений. Платон выводил ее из идеальности предмета математики, из того факта, что математика не опирается на призрачные и переменчивые данные чувственного опыта. Чертежи и символы, по Платону, являются лишь вспомогательным средством для математики, настоящие объекты, с которыми он оперирует, содержатся в его воображении и представляют собой результат восприятия разумом мира идей подобно тому, как чувственный опыт есть результат восприятия органами чувств материального мира. Нельзя не согласиться с тем, что воображение играет в работе математика решающую роль (как, впрочем, и во всех областях творческой деятельности). Правда, говорить, что математические объекты содержатся в воображении не совсем правильно: в основном они все-таки содержатся в чертежах и текстах, а воображение выхватывает их лишь небольшими частями. Мы не содержим, а, скорее, пропускаем математические объекты через воображение, и свойства нашего воображения определяют функционирование математического языка. Что же касается источника, определяющего содержание нашего воображения, то тут мы фундаментально расходимся с Платоном: источником является тот же чувственный опыт, что и в эмпирических науках. Поэтому математика создает — хотя и через посредство воображения — модели все того же, единственно существующего (насколько нам известно) мира, в котором мы живем.

Рис. 10.3. Построение равностороннего треугольника

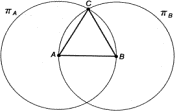
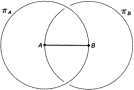
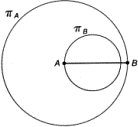
Надо сказать, что греческие математики, создав изумительное по красоте здание логически строгих доказательств, все же оставили в нем ряд дырок, причем дырки эти лежат, как мы уже отмечали, в самых нижних этажах здания — в области определений и элементарнейших свойств геометрических фигур. А это и свидетельствует о завуалированном обращении к столь презираемому платониками чувственному опыту. Математика времен Платона дает даже более яркий материал, чем современная математика, для опровержения тезиса о её независимости от опыта.

Первое доказываемое предложение первой книги Евклида содержит способ построения равностороннего треугольника по заданной его стороне. Способ таков (рис. 10.3). Пусть AB — заданная сторона треугольника. Из точки A, взятой в качестве центра, опишем окружность π_A радиуса AB. Такую же окружность (π_B) опишем из точки B. Обозначим через C любую из точек пересечения этих окружностей. Треугольник ABC равносторонний, ибо AC = CВ = AB.

В этом рассуждении есть логическая дырка: откуда следует, что построенные нами окружности вообще пересекутся? Вопрос этот чрезвычайно каверзный, ибо факт наличия точки пересечения C нельзя отнести ни к свойствам окружности, ни даже к свойствам пары окружностей (ибо они отнюдь не всегда пересекаются); мы имеем здесь дело с более специфическим свойством данной ситуации. Вероятно, Евклид чувствовал наличие здесь дырки, но не нашел, чем ее заткнуть.

Откуда же у нас уверенность, что окружности π_A и π_B пересекаются? В конечном счете, разумеется, из опыта. Из опыта созерцания и рисования прямых, окружностей и линий вообще. Из безуспешных попыток провести окружности π_A и π_B таким образом, чтобы они не пересекались.

Итак, мнение Платона о полной независимости, современной ему математики от опыта нельзя признать обоснованным. Однако вопрос о природе математической достоверности требует дальнейшего исследования, ибо просто сослаться на опыт и приравнять тем самым математическую достоверность эмпирической достоверности значило бы броситься в крайность, противоположную платонизму. Ведь мы ясно ощущаем, что математическая достоверность чем-то отличается от эмпирической. Чем же?

Утверждение, что окружности радиуса AB с центрами в A и B пересекаются (мы будем для краткости обозначать это утверждение через E₁), представляется нам если не совсем, то почти абсолютно достоверным, мы просто не можем себе представить, чтобы они не пересеклись. Не можем себе представить… Этим-то и отличается математическая достоверность от эмпирической! Когда мы говорим о завтрашнем восходе солнца, мы можем представить, что солнце не взойдет. И только на основании опыта мы полагаем, что оно, вероятно, взойдет. Здесь есть две возможности, и предсказание, какая из них осуществится, имеет вероятностный характер. Когда же мы говорим, что дважды два — четыре и что окружности, построенные так, как было указано выше, пересекаются, мы не можем представить, чтобы было иначе. Мы не видим другой возможности, поэтому и утверждения эти воспринимаем как абсолютно достоверные и независимые от конкретных наблюденных нами фактов.

10.7. В поисках аксиом

Для понимания природы математической достоверности очень поучительно довести до конца разбор утверждения E₁. Поскольку у нас все-таки остались некоторые сомнения относительно абсолютной необходимости пересечения окружности на рис. 10.3, попробуем представить себе ситуацию, когда они не пересекаются. Полная неудача этой попытки будет означать, что утверждение E₁ математически достоверно и не может быть разложено на более простые утверждения; тогда его следует принять в качестве аксиомы. Если же нам ценой большего или меньшего насилия над воображением удастся представить себе ситуацию, в которой π_A и π_B не пересекаются, эта ситуация, надо полагать, придет в противоречие с какими-то более простыми и глубокими утверждениями, обладающими математической достоверностью; тогда мы их и примем за аксиомы, а наличие противоречия будет служить доказательством E₁. Таков обычный путь к установлению аксиом в математике.

Проведем сначала окружность π_A. Затем поставим опорную ножку циркуля в точку B, а пишущую — в точку A и начнем проводить окружность π_B. Мы движемся от центра окружности π_A к ее периферии и в некоторый момент (так мы представляем это в своем воображении) должны либо пересечь окружность π_A, либо как-то перескочить через нее, разорвав для этого окружность π_A и π_B (рис. 10.4). Но окружность π_A мы воображаем как непрерывную линию и нам становится ясно, что свойства непрерывности, являющиеся более фундаментальными и общими, чем другие особенности данной задачи, лежат в основе нашей уверенности в пересечении окружностей π_A и π_B. Поэтому поставим перед собой цель доказать утверждение e₁ исходя из свойств непрерывности окружности. Нам понадобятся при этом некоторые соображения, связанные с порядком расположения точек на прямой. Понятие непрерывности и порядка мы включаем в число основных неопределяемых понятий геометрии, подобно понятиям точки, прямой, расстояния и т. д.

Рис. 10.4. «Перескакивающие» окружности

Вот один из возможных путей к цели.

Введем понятие «внутри» (применительно к окружности) с помощью следующего определения:

O₁: Говорят, что точка A лежит внутри окружности π, если она не лежит на π и любая прямая, проходящая через точку A, пересекает π двух точках, причем таким образом, что точка A лежит между точками пересечения. Если точка лежит не на окружности и не внутри нее, то говорят, что она лежит вне окружности. Понятие «между» характеризует порядок расположения трех точек на прямой. Можно принять его за основное, а можно выразить через более общее понятие «порядок» путем следующего определения:

O₂: Говорят, что точка A находится между точками B₁ и B₂, если эти три точки расположены на одной прямой и при движении по ней встречаются в порядке B₁, A, B₂ или B₂, A, B₁

Примем в качестве аксиом следующие положения:

A₁: Центр окружности лежит внутри нее.

A₂: Дуга окружности, соединяющая любые ее точки, непрерывна.

A₃: Если точка A лежит внутри окружности π, а точка B - вне окружности и эти две точки соединяет непрерывная линия, то существует точка пересечения этой линии с окружностью.

Опираясь на эти аксиомы, приступаем к доказательству. Окружность π_B по условию задачи проходит через центр A окружности π_A. Если у нас будет уверенность, что существует хотя бы одна точка окружности π_B, не лежащая внутри π_A, то мы докажем E₁. Действительно, если она лежит на π_A, то E₁ уже имеет место. Если она лежит вне π_A, то дуга окружности π_B соединяет ее с центром, т. е. с внутренней точкой окружности π_A. Следовательно, по аксиомам A₂ и A₃ существует точка пересечения π_A и π_B.

Но можем ли мы быть уверены, что существует точка на окружности π_B, находящаяся вне π_A? Попытаемся вообразить противоположный случай. Он представлен на рис. 10.5. Это вторая попытка вообразить ситуацию, противоречащую доказываемому утверждению. Если первая попытка немедленно вступила в явное противоречие с непрерывностью окружности, то вторая оказалась более успешной. В самом деле, мы с некоторой натяжкой можем представить, что так получится. Берем циркуль, острие его ставим в точку B, карандаш — в точку A. Начинаем проводить окружность, не отрывая карандаша от бумаги, а когда карандаш возвращается на уже начерченную линию, снимаем циркуль и видим, что получился рис. 10.5. А почему бы и нет?

Рис. 10.5. Окружность πB внутри πA

Рис. 10.6. К доказательству теоремы T1

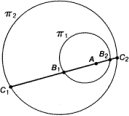
Чтобы доказать, что это невозможно, надо доказать, что в этом случае центр окружности π_B обязательно окажется вне ее. Нам поможет в этом следующая теорема:

T₁: Если окружность π₁ лежит целиком внутри окружности π₂, то каждая внутренняя точка окружности π₁ является также внутренней точкой окружности π₂.

Для ее доказательства выберем произвольную внутреннюю точку A окружности π₁ (рис. 10.6). Проведем через нее прямую. По определению O₁ она пересечет π₁ в двух точках: B₁ и B₂. Так как B₁ (как и B₂) лежит внутри π₂, эта прямая пересечет также π₂ в двух точках: C₁ и C₂. Мы получили пять точек на прямой, связанных следующими отношениями порядка: A лежит между B₁ и B₂; B₁ и B₂ лежат между C₁ и C₂. Тот факт, что в этой ситуации точка A оказывается между точками C₁ и C₂ представляется нам столь очевидным и первичным, что мы смело формулируем его как еще одну аксиому.

A₄: Если на одной прямой обе точки B₁ и B₂ лежат между точками C₁ и C₂, то и любая точка A, лежащая между B₁ и B₂, лежит также между C₁ и C₂.

Поскольку в качестве A мы можем взять любую точку внутри π₁ и провести через нее любую прямую, теорема T₁ доказана.

Теперь легко закончить доказательство E₁. Если окружность π_B лежит целиком внутри π_A, то по теореме T₁ и центр ее B должен лежать внутри π_B. Однако по условию задачи точка B находится на π_A. Следовательно, π_B содержит хотя бы одну точку, не являющуюся внутренней к π_A.

Итак, чтобы доказать одно утверждение E₁ нам понадобилось целых четыре утверждения A₁ — A₄, но зато эти утверждения выражают чрезвычайно глубокие и общие модели действительности, связанные с понятиями непрерывности и порядка. Мы не можем даже представить себе, чтобы они были ложными. Некоторые претензии можно предъявить разве только к аксиоме A₁, которая связывает понятие центра, имеющее метрическую природу (т. е. включающее понятие измерения), с понятием «внутри», опирающимся исключительно на понятия непрерывности и порядка. Можно пожелать, чтобы эта связь была осуществлена с помощью более простых геометрических объектов в более легких условиях для работы воображения. Пожелание это легко выполнимо. Заменим аксиому A₁ следующей аксиомой

A'₁ : Если на прямой дана точка A и некоторое расстояние (отрезок) Р, то существует ровно две точки на прямой, расположенные на расстоянии Р от точки A, причем точка A лежит между этими двумя точками.

Опираясь на эту аксиому, докажем утверждение A₁ как теорему. Проведем через центр окружности произвольную прямую. По аксиоме A'₁, на ней будут две точки, расположенные на расстоянии R (радиус окружности) от центра. Так как окружность определяется как множество точек, находящихся на расстоянии R от центра, эти точки принадлежат окружности. По аксиоме A'₁ точка центра лежит между ними и, следовательно, по определению O₁ является внутренней точкой. Таким образом, аксиома A₁ сведена к аксиоме A'₁. Попробуйте теперь вообразить точку на прямой, которая не имеет двух точек, расположенных от нее по разные стороны на заданном расстоянии!

10.8. Об аксиомах арифметики и логики

Первичные положения арифметики принципиально имеют ту же природу, что и первичные положения геометрии, но они, пожалуй, еще проще и очевидней, их отрицание еще более невообразимо, чем отрицание геометрических аксиом. Возьмем, например, аксиому, гласящую, что для любого числа a

a + 0 = a.

Число 0 изображает пустое множество. Можете ли вы представить себе, что от слияния некоторого множества с пустым множеством число элементов в нем изменится? Или вот еще одна арифметическая аксиома: для любых чисел a и b

a + (b + 1) = (a + b) + 1,

т. е. если единицу прибавить к числу b и результат сложить с а, то получим такое же число, как если бы мы сначала сложили a и b, а затем к результату прибавили единицу. Если проанализировать, почему мы не можем вообразить ситуацию, противоречащую этому утверждению, то мы увидим, что дело в тех же соображениях непрерывности, которые проявляются и в геометрических аксиомах. В процессе счета мы как бы проводим непрерывные линии, соединяющие считаемые предметы с элементами стандартного множества и, конечно, линии во времени (вспомним происхождение понятия «предмет»), непрерывность которых обеспечивает тождественность числа самому себе.

Естественный звуковой язык при перенесении его на бумагу порождает линейный язык, т. е. такую систему, все подсистемы которой суть линейные последовательности знаков. Знаки — это предметы, относительно которых предполагается только то, что мы умеем отличать одинаковые (тождественные) знаки от различных. Линейность естественных языков является результатом того, что звуковой язык развертывается во времени, а отношение следования во времени легко моделируется отношением порядка расположения на пространственной прямой. Специализация естественного языка привела к созданию математического линейного знакового языка, который в настоящее время образует основу математики.

Действуя в рамках линейных знаковых языков, мы постоянно пользуемся некоторыми их свойствами, которые представляются нам столь очевидными и само собой разумеющимися, что мы даже не даем себе труда сформулировать их в виде аксиом. Возьмем для примера такое утверждение: если к символу (знаку) B приписать слева символ A, а справа — символ C, то получится такое слово (последовательность знаков), как если к A приписать справа В, а затем C. Это и ему подобные утверждения обладают математической достоверностью, ибо мы не можем себе представить, чтобы было иначе. Один из разделов современной математики — теория полугрупп — изучает свойства линейных знаковых систем с аксиоматической точки зрения и простейшие из их свойств объявляет аксиомами.

И геометрические, и арифметические, и линейно-знаковые аксиомы имеют одну и ту же природу и опираются, в сущности, на одни и те же фундаментальные понятия, такие как тождество, движение, непрерывность, порядок. Никакой принципиальной разницы между этими группами аксиом нет. И если выбирать для них какой-то один термин, то их следовало бы назвать геометрическими или геометрически-кинематическими, так как все они отражают свойства нашего пространственно-временного опыта и пространственно-временного воображения. Более или менее значительное различие можно обнаружить лишь в группе «собственно геометрических» аксиом: некоторые аксиомы, касающиеся прямых и плоскостей, отражают более специфический опыт, связанный с существованием твердых тел. То же относится, по-видимому, и к метрическим понятиям. Впрочем, и это различие довольно условное. Можем ли мы говорить что-нибудь всерьез о тех понятиях, которые мы имели бы, если бы в мире не было твердых тел?

До сих пор речь шла лишь об абсолютной достоверности аксиом. А откуда у нас уверенность в достоверности утверждений, полученных из аксиом путем логического вывода?

Из того же источника: наше воображение отказывается допускать ситуацию, когда путем логического вывода мы из верных посылок получаем неверные результаты. Логический вывод состоит из последовательных шагов. На каждом шаге мы, опираясь на предшествующие утверждения, получаем новое утверждение. Из разбора формального логического вывода, который мы отложим до следующей главы, будет видно, что наша уверенность в том, что на каждом шаге мы из истинных утверждений можем получить только истинное утверждение, основывается на логических аксиомах², которые представляются нам столь же достоверными, как и рассмотренные выше математические аксиомы, и по той же причине - абсолютной невообразимости противоположной ситуации.

Имея эту уверенность, мы приобретаем уверенность, что сколько бы шагов ни содержал бы логический вывод, он все равно будет обладать этим свойством. Здесь мы используем следующую важнейшую аксиому.

Аксиома индукции: Допустим, что функция f(x) оставляет неизменным свойство Р(х), т. е.

(∀х){P(x)) ⊃ P[f(x)]}.

Обозначим через fⁿ(x) результат последовательного n-кратного применения функции f(x), т. е.

f¹(x) = f(x), fⁿ(x) = f[fⁿ(x)].

Тогда при любом n функция fⁿ(x) также оставляет неизменным свойство P(x), т. е.

(∀n)(∀х){P(x) ⊃ P[fⁿ(x)]}.

По своему происхождению и характеру логические аксиомы и аксиома индукции (которую относят к арифметике, так как она включает понятие числа) ничем не отличаются от остальных аксиом: все они суть математические аксиомы. Различие существует лишь в характере их использования. Когда математические аксиомы применяются к математическим утверждениям, они становятся элементами метасистемы. в рамках системы математически достоверных утверждений и мы называем их логическими аксиомами. Благодаря этому система математически достоверных утверждений становится способной к развитию. Великое открытие греков состояло в том, что можно прилагать достоверное к достоверному, и получать таким образом новое достоверное.

10.9. Сваи, уходящие вглубь

Описание математических аксиом как моделей действительности, которые истинны не только в сфере реального опыта, но и в сфере воображения, опирается на их субъективное восприятие. Можно ли дать им более объективную характеристику. Воображение возникает на определенном этапе развития нервной системы как произвольное ассоциирование представлений. Предыдущим этапом был этап непроизвольного ассоциирования (уровень собаки). Естественно предположить, что переход от непроизвольного ассоциирования к произвольному не произвел существенной перемены в том материале, который имеется в распоряжении ассоциирующей системы, т. е. в представлениях, образующих ассоциации,— это следует из иерархического принципа устройства и развития нервной системы, при котором надстройка верхних этажей слабо влияет на нижние. Из того же принципа следует, что в процессе предыдущего перехода — от фиксированных понятий к непроизвольному ассоциированию — самые нижние уровни системы понятий остались неизменными и обусловили те всеобщие глубокие свойства представлений, которые были в наличии и до ассоциирования и которые ассоциирование изменить не может. Не может изменить их и воображение. Эти свойства инвариантны относительно преобразований, осуществляемых воображением. На них-то и опираются математические аксиомы. Если представить себе деятельность воображения как перетасовку и склейку каких-то элементов, «кусков» чувственного восприятия, то аксиомы — это модели, которые истинны для каждого куска и поэтому — для любой их комбинации. Способность воображения разрезать чувственный опыт на куски не безгранична, ибо, возникая на некотором этапе развития, оно принимает уже существующую систему понятий как некий фон, как основу, не подлежащую переделке. Такие глубокие понятия, как движение, тождество, непрерывность, заложены были в этом фоне, поэтому и модели, опирающиеся на эти понятия, оказываются универсально истинными не только для реального опыта, но и для любых конструкций, которые способно создать воображение. Математика образует каркас здания естественных наук. Ее аксиомы — это сваи, уходящие в самую глубь нейронных понятий, ниже того уровня, где начинает хозяйничать воображение. Отсюда та прочность основы, которая отличает математику от эмпирического знания. Она пренебрегает поверхностными ассоциациями, составляющими каждодневный жизненный опыт, предпочитая продолжать строительство костяка системы понятий, начатого природой и заложенного в нижние уровни иерархии. И уже на этом костяке будут образовываться «необязательные» модели, которые мы относим к естественным наукам, как на базе врожденных и «обязательных» понятий низшего уровня образуются «необязательные» ассоциации представлений, составляющие содержание жизненного опыта. Требования, диктуемые математикой, обязательны; строя модели действительности, мы не можем обойти их, если бы даже захотели. Поэтому возможную неистинность теории мы всегда выносим за пределы сферы действия математики. Если обнаруживается расхождение между теорией и экспериментом, изменяют внешнюю, «необязательную» часть теории, но никому не приходит в голову высказать предположение, что в данном случае оказалось неверным равенство 2 + 2 = 4.

«Обязательность» классических математических моделей не противоречит появлению математических и физических теорий, которые, на первый взгляд, вступают в конфликт с нашей пространственно-временной интуицией (например, неевклидова геометрия или квантовая механика). Эти теории суть языковые модели действительности, полезность которых проявляется не в сфере повседневного опыта, а в весьма специальных ситуациях. Они не разрушают и не заменяют классических моделей, а продолжают их. Так, квантовая механика опирается на классическую. А какая теория может обойтись без арифметики? Парадоксы и противоречия возникают тогда, когда мы забываем, что понятия-конструкты, входящие в новую теорию, это — новые понятия, если даже их обозначают старыми именами. Мы говорим о «прямой» в неевклидовой геометрии и называем электрон «частицей», хотя языковая деятельность, связанная с этими словами, — доказательство теорем и квантово-механические выкладки — совсем не такая, как в прежних теориях, из которых были заимствованы термины. Если дважды два не равно четырем, то либо два — не два, либо «жды» — не «жды», либо четыре — не четыре.

Особую роль математики в процессе познания можно выразить в виде утверждения, что математические понятия и аксиомы представляют собой не результат, а условие и форму познания действительности. Эта мысль была развита Кантом, и с ней можно согласиться, если рассматривать человека как полностью данное существо и не задавать себе вопроса: а почему человеку свойственны эти условия и формы познания? Но, задав этот вопрос, мы должны прийти к выводу, что они сами являются моделями действительности, выработанными в процессе эволюции (который в одном из важных своих аспектов есть не что иное, как процесс познания мира живыми структурами). С точки зрения законов природы принципиальной разницы между математическими и эмпирическими моделями нет; это разграничение отражает лишь наличие в устройстве человеческого мозга черты, отделяющей врожденные модели от благоприобретенных. Положение этой черты, надо полагать, содержит элемент исторической случайности. Проходи она в другом уровне, мы, возможно, были бы не в силах вообразить, что солнце может не взойти или что человек может парить над землей, как будто силы тяжести не существует.

10.10. Платонизм в ретроспективе

Идеализм Платона — результат своеобразной проекции элементов языка в действительность. «Идеи» Платона имеют то же происхождение, что и духи первобытного мышления, — это воображаемые значения реально существующих имен. На первых этапах развития критического мышления еще не существует правильного понимания природы абстрагирования и взаимоотношения между языковыми объектами и неязыковой деятельностью. Первобытный комплекс имя-значение еще навязывает представление о взаимно однозначной связи между именем и значением. Для слов, обозначающих определенный, единственный предмет, взаимная однозначность как будто имеет место, ибо предмет мы представляем себе как что-то одно. А как быть с общими понятиями (универсальными)? В сфере реально существующего для значений вообще не остается места, все расхватано «единичными» понятиями — ведь к каждому предмету можно подкрепить бирку с именем. Образующуюся пустоту и заполняет «идея». Подчеркнем, что идеализм Платона отнюдь не включает утверждения о примате духовного над материальным, т. е. не является спиритуализмом (этот термин, широко используемый в западно-европейской литературе, у нас мало употребителен и часто заменяется термином «идеализм», что приводит к неточностям). Духовный опыт, по Платону, это такая же эмпирия, как чувственный опыт, и никакого отношения к миру идей не имеет. «Идеи» Платона — чистые призраки, причем призраки, порожденные не духовным, а чувственным опытом.

С современной кибернетической точки зрения единичным понятием можно считать только строго определенную, единичную ситуацию, т. е. указание всех рецепторов, образующих вход нервной системы. Нечего и говорить, что субъективно мы совершенно не осознаем единичных, в этом смысле, понятий. Близкие ситуации становятся неразличимыми где-то на самых ранних стадиях обработки информации, и представления, с которыми имеет дело наше сознание, это обобщенные состояния, т. е. общие, или абстрактные понятия (множество ситуаций). Понятия об определенных предметах, которые традиционная логика наивно принимает за первичные элементы чувственного опыта и называет «единичными» понятиями, в действительности, как показано выше, являются весьма сложными конструкциями, требующими анализа киноленты ситуаций и опирающимися на более элементарные абстрактные понятия, такие, как непрерывность, форма, цвет, пространственные отношения и т. п. Причем чем «конкретнее» понятие с точки зрения логики, тем сложнее оно с точки зрения кибернетики. Так, «конкретная кошка» отличается от «просто кошки» тем, что для придания смысла первому понятию требуется более длинная кинолента ситуаций, чем второму, строго говоря даже бесконечно длинная, ибо, имея в виду конкретную кошку, мы имеем в виду не только ее «личное дело», которое ведется со дня рождения, но и всю ее генеалогию. По своей природе «конкретные» и «абстрактные» понятия ничем принципиально не различаются, и те и другие отражают свойства реального мира. Если различие и есть, то оно противоположно тому, которое усматривает традиционная логика: абстрактные общие понятия чувственного и духовного опыта (не смешивать с конструктами математики!) проще и ближе к природе, чем конкретные понятия, связанные с определенными предметами. Логиков ввело в заблуждение то обстоятельство, что в языке конкретные понятия появляются раньше, чем абстрактные. Но это как раз свидетельствует об их относительно более высоком положении в иерархии нейронных понятий-положений, благодаря которому они оказались на стыке с языковыми понятиями.

Платоновская теория идей, постулировав вымышленное идеальное бытие обобщенных предметов, поставила одноместные предикаты (свойства) в выделенное положение по сравнению с многоместными предикатами (отношениями), она придала свойствам статус истинного бытия, в котором отказала отношениям. Это со всей наглядностью проявилось в логике Аристотеля. Отсюда предметность и статичность мышления, столь характерная для греков классического периода. В следующей главе мы увидим, как этот образ мышления отразился на развитии математики.

¹ Созвучие с русским не случайно, это древний индоевропейский корень (ср. лат. vidi — увидел).

² Для знакомых с математической логикой заметим: в широком смысле, включая правила вывода.