|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Задача о разборчивой невесте // Сабир Гусейн-Заде |
Задача о разборчивой невестеСабир Гусейн-Заде
Примерно 40 лет тому назад Мартин Гарднер придумал такую задачу: “В некотором царстве, в некотором государстве пришло время принцессе выбирать себе жениха. В назначенный день явились 1000 царевичей и королевичей, их построили в очередь в случайном порядке и стали по одному приглашать к принцессе. Про любых двух претендентов принцесса, познакомившись с ними, может сказать, какой из них лучше. Познакомившись с претендентом, принцесса может либо принять предложение (и тогда выбор сделан навсегда), либо отвергнуть его (и тогда претендент потерян: царевичи и королевичи гордые и не возвращаются). Какой стратегии должна придерживаться принцесса, чтобы с наибольшей вероятностью выбрать лучшего из претендентов?”. В 1965 году её формулировку и решение рассказал на своём семинаре Е. Б. Дынкин. Но его метод был необобщаем на другие варианты задачи: например, когда целью является выбор не наилучшего, а одного из трёх лучших. В таком виде задача была решена лектором при помощи метода, который легко переносится и на ряд близких задач. Так из полушуточной задачи вырос новый раздел математики — теория оптимальной остановки случайных процессов. Формально задача может быть сформулирована следующим образом:
В 1963 году академик РАН Евгений Дынкин предложил решение этой задачи для частного случая. Общее решение было найдено Сабиром Гусейн-Заде в 1966 году. Этой задаче было уделено много внимания во многом потому, что оптимальная стратегия имеет интересную особенность: если число кандидатов достаточно велико (порядка сотни), оптимальная стратегия будет заключаться в том, чтобы отклонить всех первых Примечательно, что диссертация член-корреспондента РАН Бориса Березовского на соискание ученой степени доктора наук «Разработка теоретических основ алгоритмизации принятия предпроектных решений и их применения», защищенная в 1983 году, является обобщением задачи о разборчивой невесте. Гусейн-Заде Сабир Меджидович, доктор физико-математических наук, профессор.
Популярные лекции по математике на Малом мехмате МГУ, г. Москва, 30 ноября 2002 г.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Задача о разборчивой невесте // Сабир Гусейн-Заде |
|
[time: 11 ms; queries: 8]
10 Мар 2026 23:53:16 GMT+3 |


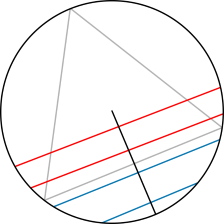 Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Наудачу выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника. Бертран предложил три решения, дающие различный результат.
Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Наудачу выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника. Бертран предложил три решения, дающие различный результат. Сегодня я хочу рассказать вам о математике любви. Думаю, все согласятся с тем, что математики широко известны своими успехами на любовном поприще. Но причина не только в нашей решительности, отличных навыках поддержания беседы и красивых пеналах. Причина также и в том, что мы немало поработали над математикой поиска идеальной пары.
Сегодня я хочу рассказать вам о математике любви. Думаю, все согласятся с тем, что математики широко известны своими успехами на любовном поприще. Но причина не только в нашей решительности, отличных навыках поддержания беседы и красивых пеналах. Причина также и в том, что мы немало поработали над математикой поиска идеальной пары.