Найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков

Сообщения: 1 🔎

# 5 Мая 2015 01:23:42
Evgeniy

Задача

Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная, творожная и мясная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.

Вид начинки	Себестоимость (за 1 тонну)	Отпускная цена (за 1 тонну)	Производственные возможности
ягоды	70 тыс. руб.	100 тыс. руб.	90 (тонн в мес.)
творог	100 тыс. руб.	135 тыс. руб.	75 (тонн в мес.)
мясо	110 тыс. руб.	145 тыс. руб.	60 (тонн в мес.)

Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц.

Решение

Пусть $x,y,z$ — соответственно кол-во тыс. ягодных, творожных и мясных блинов, производимых в месяц.

Установим связь между возможным количеством производимых блинов. Производство 1 тыс. ягодных, творожных и мясных блинов соответственно занимает $\dfrac{1}{90}$ , $\dfrac{1}{75}$ и $\dfrac{1}{60}$ производственной мощности фабрики.

Если фабрика работает на полную нагрузку, то кол-во блинов разных сортов связано соотношением

$\frac{1}{90}x+\frac{1}{75}y+\frac{1}{60}z=1$ .

Кроме этого должны быть выполнены условия $x\ge 15$ , $y\ge 15$ , $z\ge 15$ .

Прибыль фабрики выражается так $s(x,y,z)=30x+35y+35z$ .

Для решения задачи нужно найти максимум так называемой целевой функции $s(x,y,z)=30x+35y+35z$ на множестве, определенном следующими условиями:

$\left\{\begin{aligned} &\frac{1}{90}x+\frac{1}{75}y+\frac{1}{60}z=1\\ &x\ge15\\ &y\ge15\\ &z\ge15\\ \end{aligned}\right.$

Это множество представляет собой треугольник на плоскости $\frac{1}{90}x+\frac{1}{75}y+\frac{1}{60}z=1$ , образованный линиями пересечения этой плоскости с плоскостями $x=15$ , $y=15$ , $z=15$ . На рисунке этот треугольник заштрихован.

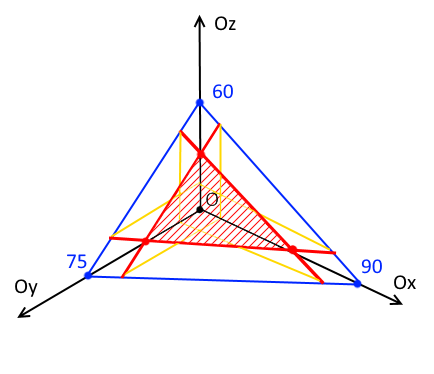
https://img-fotki.yandex.ru/get/3001/311305945.0/0_fa441_e3d572c8_orig.png

Максимум линейной функции достигается на вершинах (возможно, на сторонах) этого треугольника.

Найдем вершины треугольника и посчитаем значения целевой функции $s$ в них.

Эти три точки определяются, соответственно, условиями

$\left\{\begin{aligned} &\frac{1}{90}x+\frac{1}{75}y+\frac{1}{60}z=1\\ &x = 15\\ &y = 15\\ \end{aligned}\right.$

$\left\{\begin{aligned} &\frac{1}{90}x+\frac{1}{75}y+\frac{1}{60}z=1\\ &x = 15\\ &z = 15\\ \end{aligned}\right.$

$\left\{\begin{aligned} &\frac{1}{90}x+\frac{1}{75}y+\frac{1}{60}z=1\\ &y = 15\\ &z = 15\\ \end{aligned}\right.$

Решая системы, находим

$%\icomma$ A_1=(15;15;38);\\ A_2=(15;43,75;15);\\ A_3=(15;15;49,5) $%$

$%\icomma$ s(A_1)=30 \cdot 15+35 \cdot 15+35 \cdot 38=2305;\\ s(A_2)=30 \cdot 15+35 \cdot 43,75+35 \cdot 15=2506,25;\\ s(A_3)=30 \cdot 15+35 \cdot 15+35 \cdot 49,5=2535 $%$

Как видно, максимум прибыли достигается при $x=15, y=15, z=49{,}5$ и равен $2535$ тыс. руб.

Цитировать

Сообщения: 1 🔎


*Имя:
Заголовок:
[tex-clear] [tex-help] [ted] formulas > Формат Шрифт $\mathit{}$ $\mathbf{}$ $\mathrm{}$ $\mathsf{}$ $\mathfrak{}$ $\mathbb{}$ $\mathcal{}$ $\mathscr{}$ Размер $\tiny Aa$ $\scriptsize Aa$ $\footnotesize Aa$ $\small Aa$ $\normalsize Aa$ $\large Aa$ $\Large Aa$ $\LARGE Aa$ $\huge Aa$ $\Huge Aa$ Цвет ${\color{Red} }$ ${\color{DarkRed} }$ ${\color{BrickRed} }$ ${\color{Magenta} }$ ${\color{VioletRed} }$ ${\color{Yellow} }$ ${\color{Orange} }$ ${\color{DarkOrange} }$ ${\color{Brown} }$ ${\color{Sepia} }$ ${\color{Green} }$ ${\color{DarkGreen} }$ ${\color{ForestGreen} }$ ${\color{Teal} }$ ${\color{Emerald} }$ ${\color{Blue} }$ ${\color{DarkBlue} }$ ${\color{RoyalBlue} }$ ${\color{BlueViolet} }$ ${\color{Purple} }$ ${\color{Gray} }$ ${\color{Plum} }$ ${\color{Cyan} }$ Стиль \text{} $\tstyle$ $\dstyle$ Дроби, корни $\frac{}{}$ $\tfrac{}{}$ $\dfrac{}{}$ $\cfrac{}{}$ $\over$ $\atop$ $\sqrt{}$ $\sqrt[]{}$ $\binom{}{}$ $\tbinom{}{}$ Скобки $()$ $\{\}$ $[]$ $\|\|$ $\\|\\|$ $\langle \rangle$ $\left( \right)$ $\left\{ \right\}$ $\left[ \right]$ $\left\| \right\|$ $\left\\| \right\\|$ $\left\langle \right\rangle$ $\left( \right.$ $\left. \right)$ $\left\{ \right.$ $\left. \right\}$ $\left[ \right.;$ $\left. \right]$ $\left\| \right.;$ $\left. \right\|$ Декор., индексы $^{}$ $_{}$ $^{}_{}$ ${}^{}$ ${}_{}$ ${}^{}_{}$ $\leftidx{}{}{}$ $\ltrans{}$ $\vec{}$ $\bar{}$ $\tilde{}$ $\hat{}$ $\dot{}$ $\ddot{}$ $\dddot{}$ $^{\circ}$ $\overset{\circ}{}$ $\overset{\frown}{}$ $\overrightarrow{}$ $\overleftarrow{}$ $\overline{}$ $\underline{}$ $\widetilde{}$ $\widehat{}$ $\overbrace{}^{}$ $\underbrace{}_{}$ $\overset{}{}$ $\underset{}{}$ $\left. \right\|_{}^{}$ $\left. \right\|_{}$ $\not{}$ $\cancel{}$ $\bcancel{}$ $\xcancel{}$ Пробелы, разд. $\!$ $x y$ $\,$ $\;$ $\$ $\quad$ $\qquad$ $\cdot$ $\dots$ $\cdots$ $\ddots$ $\vdots$ $\colon$ $\mid$ \phantom{} \mathstrut{} Квант., операц. $\forall$ $\exists$ $\exists!$ $\nexists$ $\lnot$ $\land$ $\lor$ $\cup$ $\cap$ $\sqcup$ $\sqcap$ $\setminus$ $\bigtriangleup$ $\uplus$ $\cdot$ $\circ$ $\times$ $\pm$ $\mp$ $\dotplus$ $\div$ $/$ $\neg$ $\wedge$ $\vee$ $\barwedge$ $\veebar$ $\curlywedge$ $\curlyvee$ $\textasciicircum$ $\oplus$ $\ominus$ $\otimes$ $\oslash$ $\odot$ $\circledcirc$ $\circledast$ Отношения $\in$ $\notin$ $\ni$ $\not\ni$ $\subset$ $\supset$ $\not\subset$ $\not\supset$ $\subseteq$ $\supseteq$ $\nsubseteq$ $\nsupseteq$ $\subsetneq$ $\supsetneq$ $\subsetneqq$ $\supsetneqq$ $\neq$ $\approx$ $\equiv$ $\not\equiv$ $\sim$ $\nsim$ $\cong$ $\ncong$ $\leqslant$ $\geqslant$ $\nleqslant$ $\ngeqslant$ $\le$ $\ge$ $\nleq$ $\ngeq$ $\nless$ $\ngtr$ $\lneq$ $\gneq$ $\lneqq$ $\gneqq$ $\ll$ $\gg$ $\prec$ $\succ$ $\nprec$ $\nsucc$ $\preceq$ $\succeq$ $\npreceq$ $\nsucceq$ $:=$ $\overset{\mathrm{def}}{=}$ $\triangleq$ $\models$ $\vdash$ $\dashv$ $\mid$ $\nmid$ $\mathop{\vdots}$ $\mathop{\not\vdots}$ $\parallel$ $\nparallel$ $\perp$ $\not\perp$ Большие операт. $\sum_{}^{}$ $\sum_{}$ $\prod_{}^{}$ $\prod_{}$ $\bigcup_{}^{}$ $\bigcup_{}$ $\bigcap_{}^{}$ $\bigcap_{}$ $\bigsqcup_{}^{}$ $\biguplus_{}^{}$ $\bigvee_{}^{}$ $\bigwedge_{}^{}$ $\bigoplus_{}^{}$ $\bigotimes_{}^{}$ $\bigodot_{}^{}$ Стрелки $\to$ $\mapsto$ $\rightarrow$ $\leftarrow$ $\leftrightarrow$ $\nrightarrow$ $\nleftarrow$ $\nleftrightarrow$ $\Rightarrow$ $\Leftarrow$ $\Leftrightarrow$ $\nRightarrow$ $\nLeftarrow$ $\nLeftrightarrow$ $\Uparrow$ $\Downarrow$ $\Updownarrow$ $\rightrightarrows$ $\longmapsto$ $\longrightarrow$ $\longleftarrow$ $\longleftrightarrow$ $\uparrow$ $\downarrow$ $\updownarrow$ $\Longrightarrow$ $\Longleftarrow$ $\Longleftrightarrow$ $\implies$ $\iff$ $\rightleftarrows$ $\nearrow$ $\swarrow$ $\nwarrow$ $\searrow$ $\circlearrowleft$ $\circlearrowright$ $\curvearrowleft$ $\curvearrowright$ $\xrightarrow[]{}$ $\xleftarrow[]{}$ Буквы, значки Греческие $\Gamma$ $\Delta$ $\Theta$ $\Lambda$ $\Xi$ $\Pi$ $\Sigma$ $\Upsilon$ $\Phi$ $\Psi$ $\Omega$ $\digamma$ $\alpha$ $\beta$ $\gamma$ $\delta$ $\epsilon$ $\varepsilon$ $\zeta$ $\eta$ $\theta$ $\vartheta$ $\iota$ $\kappa$ $\varkappa$ $\lambda$ $\mu$ $\nu$ $\xi$ $\pi$ $\varpi$ $\rho$ $\varrho$ $\sigma$ $\varsigma$ $\tau$ $\upsilon$ $\phi$ $\varphi$ $\chi$ $\psi$ $\omega$ Резные $\mathbb{A}$ $\mathbb{B}$ $\mathbb{C}$ $\mathbb{D}$ $\mathbb{E}$ $\mathbb{F}$ $\mathbb{G}$ $\mathbb{H}$ $\mathbb{I}$ $\mathbb{J}$ $\mathbb{K}$ $\mathbb{L}$ $\mathbb{M}$ $\mathbb{N}$ $\mathbb{O}$ $\mathbb{P}$ $\mathbb{Q}$ $\mathbb{R}$ $\mathbb{S}$ $\mathbb{T}$ $\mathbb{U}$ $\mathbb{V}$ $\mathbb{W}$ $\mathbb{X}$ $\mathbb{Y}$ $\mathbb{Z}$ Калиграф. $\mathcal{A}$ $\mathcal{B}$ $\mathcal{C}$ $\mathcal{D}$ $\mathcal{E}$ $\mathcal{F}$ $\mathcal{G}$ $\mathcal{H}$ $\mathcal{I}$ $\mathcal{J}$ $\mathcal{K}$ $\mathcal{L}$ $\mathcal{M}$ $\mathcal{N}$ $\mathcal{O}$ $\mathcal{P}$ $\mathcal{Q}$ $\mathcal{R}$ $\mathcal{S}$ $\mathcal{T}$ $\mathcal{U}$ $\mathcal{V}$ $\mathcal{W}$ $\mathcal{X}$ $\mathcal{Y}$ $\mathcal{Z}$ Рукописные $\mathscr{A}$ $\mathscr{B}$ $\mathscr{C}$ $\mathscr{D}$ $\mathscr{E}$ $\mathscr{F}$ $\mathscr{G}$ $\mathscr{H}$ $\mathscr{I}$ $\mathscr{J}$ $\mathscr{K}$ $\mathscr{L}$ $\mathscr{M}$ $\mathscr{N}$ $\mathscr{O}$ $\mathscr{P}$ $\mathscr{Q}$ $\mathscr{R}$ $\mathscr{S}$ $\mathscr{T}$ $\mathscr{U}$ $\mathscr{V}$ $\mathscr{W}$ $\mathscr{X}$ $\mathscr{Y}$ $\mathscr{Z}$ Готические $\mathfrak{A}$ $\mathfrak{B}$ $\mathfrak{C}$ $\mathfrak{D}$ $\mathfrak{E}$ $\mathfrak{F}$ $\mathfrak{G}$ $\mathfrak{H}$ $\mathfrak{I}$ $\mathfrak{J}$ $\mathfrak{K}$ $\mathfrak{L}$ $\mathfrak{M}$ $\mathfrak{N}$ $\mathfrak{O}$ $\mathfrak{P}$ $\mathfrak{Q}$ $\mathfrak{R}$ $\mathfrak{S}$ $\mathfrak{T}$ $\mathfrak{U}$ $\mathfrak{V}$ $\mathfrak{W}$ $\mathfrak{X}$ $\mathfrak{Y}$ $\mathfrak{Z}$ $\mathfrak{a}$ $\mathfrak{b}$ $\mathfrak{c}$ $\mathfrak{d}$ $\mathfrak{e}$ $\mathfrak{f}$ $\mathfrak{g}$ $\mathfrak{h}$ $\mathfrak{i}$ $\mathfrak{j}$ $\mathfrak{k}$ $\mathfrak{l}$ $\mathfrak{m}$ $\mathfrak{n}$ $\mathfrak{o}$ $\mathfrak{p}$ $\mathfrak{q}$ $\mathfrak{r}$ $\mathfrak{s}$ $\mathfrak{t}$ $\mathfrak{u}$ $\mathfrak{v}$ $\mathfrak{w}$ $\mathfrak{x}$ $\mathfrak{y}$ $\mathfrak{z}$ Значки $\varnothing$ $\infty$ $\partial$ $\aleph$ $\mathfrak{c}$ $\ell$ $\hbar$ $\O$ $\bot$ $\top$ $\angle$ $\measuredangle$ $\sphericalangle$ $\frown$ $\smile$ $\vartriangle$ $\triangledown$ $\blacktriangle$ $\blacktriangledown$ $\triangleleft$ $\triangleright$ $\blacktriangleleft$ $\blacktriangleright$ $\triangle$ $\square$ $\blacksquare$ $\bigcirc$ $\star$ $\bigstar$ $\bullet$ $\diamond$ $\textasciicircum$ $\therefore$ $\because$ $\&$ $\%$ $\S$ $\P$ $\backslash$ Функции, операт. Станд. функц. $\max_{}$ $\min_{}$ $\sup_{}$ $\inf_{}$ $\Pr_{}$ $\operatorname{sign}$ $\deg$ $\arg$ $\operatorname{НОД}$ $\operatorname{НОК}$ $\operatorname{Im}$ $\operatorname{Re}$ $\dim$ $\ker$ $\hom$ $\operatorname{diag}$ $\operatorname{rank}$ $\det$ $\operatorname{tr}$ $\operatorname{spec}$ $\mathsf{P}$ $\mathsf{M}$ $\mathsf{D}$ $\Im$ $\Re$ \operatorname{} Элем. функц. $\exp$ $\log_{}$ $\ln$ $\lg$ $\sin$ $\cos$ $\tg$ $\ctg$ $\arcsin$ $\arccos$ $\arctg$ $\arcctg$ $\sh$ $\ch$ $\th$ $\cth$ Пределы $\lim_{n\to\infty}$ $\lim_{x\to }$ $lim_{}$ $\limsup_{n\to\infty}$ $\liminf_{n\to\infty}$ $\varlimsup_{n\to\infty}$ $\varliminf_{n\to\infty}$ $\to$ $\rightrightarrows$ $\infty$ Дифф. опер. $\mathrm{d}$ $\partial$ $\frac{\mathrm{d} }{\mathrm{d} x}$ $\frac{\partial }{\partial x}$ $\frac{\partial^2 }{\partial x^2}$ $\nabla$ $\Delta$ $\operatorname{grad}$ $\operatorname{div}$ $\operatorname{rot}$ Интегралы $\int$ $\int_{}^{}$ $\int\limits_{}^{}$ $\int_{}$ $\int\limits_{}$ $\oint$ $\oint_{}$ $\oint\limits_{}$ $\ointctrclockwise$ $\ointclockwise$ $\iint$ $\iint_{}$ $\iint\limits_{}$ $\oiint$ $\oiint_{}$ $\oiint\limits_{}$ $\varoiint$ $\sqiint$ $\iiint$ $\iiint_{}$ $\iiint\limits_{}$ $\dotsint$ $\dotsint_{}$ $\dotsint\limits_{}$ Сравнения $\equiv$ $\mod{}$ $\pmod{}$ $\pod{}$ Матрицы $\begin{matrix} & \\ & \end{matrix}$ $\begin{pmatrix} & \\ & \end{pmatrix}$ $\begin{vmatrix} & \\ & \end{vmatrix}$ $\begin{Vmatrix} & \\ & \end{Vmatrix}$ $\begin{bmatrix} & \\ & \end{bmatrix}$ $\begin{Bmatrix} & \\ & \end{Bmatrix}$ $\left\{\begin{matrix} & \\ & \end{matrix}\right.$ $\left[\begin{matrix} & \\ & \end{matrix}\right.$ $\left.\begin{matrix} & \\ & \end{matrix}\right\}$ $\left.\begin{matrix} & \\ & \end{matrix}\right\|$ $\left(\begin{smallmatrix} & \\ & \end{smallmatrix}\right)$ $\binom{}{}$ $\tbinom{}{}$ Спец. блоки $\begin{cases} & \\ & \end{cases}$ $\begin{aligned} & \\ & \end{aligned}$ $\begin{align} & \tag{} \\ & \tag{} \end{align}$ $\begin{tikzpicture} \end{tikzpicture}$ $\ce{}$
Преобразовать url в ссылки Преобразовать $ в tex
* Сколько символов на картинке?
Отправляя данные, вы соглашаетесь с Правилами сайта.

∀ x, y, z

Найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков