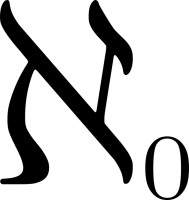Разные размерности

Сообщения: 1 🔎

# 8 Авг 2019 01:45:19
Math

Что такое размерность фигуры, то есть, грубо говоря, сколько нужно параметров, чтобы точно задать положение любой точки в этой фигуре, — вопрос отнюдь не простой, хотя интуитивно может и казаться понятным, что это такое. Математики, естественно, размышляли над ним и придумали несколько разных определений, которые в некоторых случаях могут даже давать разные численные результаты применительно к одной и той же фигуре. Это, как ни странно, вовсе не означает, что в математике что-то не так, а, наоборот, позволяет при помощи разных подходов изучать разные объекты.

Классическое определение звучит следующим образом: (топологической) размерностью (или размерностью Лебега) фигуры $F$ называется наименьшее целое число $n$ , обладающее тем свойством, что при любом $\varepsilon > 0$ существует конечный набор шаров радиуса не больше $\varepsilon$ , покрывающих фигуру $F$ так, что любая точка из $F$ принадлежит не более чем $(n + 1)$ шару. Предполагается, что шары не содержат свою границу; для плоских фигур вместо шаров можно взять круги. Например, отрезок является одномерной фигурой, потому что его можно покрыть кругами так, как показано на рис. 1: каждая точка содержится не более, чем в двух различных кругах, причем это свойство не зависит от их размера, то есть можно указать покрытие кругами любого меньшего (сколь угодно малого) размера, обладающее тем же самым свойством. Контрольный вопрос: чему равна топологическая размерность окружности?

Рис. 1. Покрытия отрезка кругами разных радиусов

Однако описанный выше способ — не единственный подход к определению размерности. Говорят, что фигура $F$ имеет фрактальную размерность $d$ , если при разбиении ее на кусочки, каждый из которых в $k$ раз меньше исходной фигуры, оказывается, что общее число кусочков равно $k^d$ . Например, отрезок является одномерной фигурой, потому что если разбить отрезок длины $1$ на отрезочки длины $1/3$ , то общее количество таких отрезочков будет $3^1 = 3$ , а если на отрезочки длины $1/10$ , то $10^1 = 10$ (и так далее для любого числа отрезочков). Точно так же, квадрат — фигура двумерная, ведь если разбить квадрат со стороной $1$ на квадратики со стороной $1/3$ , то общее количество таких квадратиков будет $3^2 = 9$ , а если на квадратики со стороной $1/10$ , то $10^2 = 100$ (и так далее).

Для большинства привычных фигур топологическая и фрактальная размерности совпадают (то есть $n = d$ ). Однако для некоторых фигур это оказывается не так: тогда как топологическая размерность всегда является целым числом, их фрактальная размерность получается дробной. Типичный пример таких фигур — собственно, фракталы.

Задача

Рассмотрим довольно известный фрактал ковер Серпинского. Он строится итеративно следующим образом. В качестве начального объекта берется квадрат. На первом шаге нужно мысленно разбить этот квадрат на 9 одинаковых квадратов, а затем (уже не мысленно, а вполне реально) удалить центральный из них. Затем, на втором шаге, каждый из оставшихся восьми квадратов также надо мысленно разделить на 9 квадратиков, после чего удалить центральный (рис. 2). На третьем шаге мы проводим ту же самую операцию с каждым из 64 оставшихся квадратиков и так далее. То, что останется в итоге после завершения этой бесконечной процедуры (то есть точки, которые принадлежат всем получающимся в процессе фигурам) и называется ковром Серпинского.

Рис. 2. Первые шаги построения ковра Серпинского

а) Покажите, что топологическая размерность квадрата (с внутренностью) равна 2.

б) Проверьте, что топологическая размерность ковра Серпинского равна 1. Чему равна его фрактальная размерность?

Хайгар Нурлигареев
«Элементы»

Цитировать

Сообщения: 1 🔎


*Имя:
Заголовок:
[tex-clear] [tex-help] [ted] formulas > Формат Шрифт $\mathit{}$ $\mathbf{}$ $\mathrm{}$ $\mathsf{}$ $\mathfrak{}$ $\mathbb{}$ $\mathcal{}$ $\mathscr{}$ Размер $\tiny Aa$ $\scriptsize Aa$ $\footnotesize Aa$ $\small Aa$ $\normalsize Aa$ $\large Aa$ $\Large Aa$ $\LARGE Aa$ $\huge Aa$ $\Huge Aa$ Цвет ${\color{Red} }$ ${\color{DarkRed} }$ ${\color{BrickRed} }$ ${\color{Magenta} }$ ${\color{VioletRed} }$ ${\color{Yellow} }$ ${\color{Orange} }$ ${\color{DarkOrange} }$ ${\color{Brown} }$ ${\color{Sepia} }$ ${\color{Green} }$ ${\color{DarkGreen} }$ ${\color{ForestGreen} }$ ${\color{Teal} }$ ${\color{Emerald} }$ ${\color{Blue} }$ ${\color{DarkBlue} }$ ${\color{RoyalBlue} }$ ${\color{BlueViolet} }$ ${\color{Purple} }$ ${\color{Gray} }$ ${\color{Plum} }$ ${\color{Cyan} }$ Стиль \text{} $\tstyle$ $\dstyle$ Дроби, корни $\frac{}{}$ $\tfrac{}{}$ $\dfrac{}{}$ $\cfrac{}{}$ $\over$ $\atop$ $\sqrt{}$ $\sqrt[]{}$ $\binom{}{}$ $\tbinom{}{}$ Скобки $()$ $\{\}$ $[]$ $\|\|$ $\\|\\|$ $\langle \rangle$ $\left( \right)$ $\left\{ \right\}$ $\left[ \right]$ $\left\| \right\|$ $\left\\| \right\\|$ $\left\langle \right\rangle$ $\left( \right.$ $\left. \right)$ $\left\{ \right.$ $\left. \right\}$ $\left[ \right.;$ $\left. \right]$ $\left\| \right.;$ $\left. \right\|$ Декор., индексы $^{}$ $_{}$ $^{}_{}$ ${}^{}$ ${}_{}$ ${}^{}_{}$ $\leftidx{}{}{}$ $\ltrans{}$ $\vec{}$ $\bar{}$ $\tilde{}$ $\hat{}$ $\dot{}$ $\ddot{}$ $\dddot{}$ $^{\circ}$ $\overset{\circ}{}$ $\overset{\frown}{}$ $\overrightarrow{}$ $\overleftarrow{}$ $\overline{}$ $\underline{}$ $\widetilde{}$ $\widehat{}$ $\overbrace{}^{}$ $\underbrace{}_{}$ $\overset{}{}$ $\underset{}{}$ $\left. \right\|_{}^{}$ $\left. \right\|_{}$ $\not{}$ $\cancel{}$ $\bcancel{}$ $\xcancel{}$ Пробелы, разд. $\!$ $x y$ $\,$ $\;$ $\$ $\quad$ $\qquad$ $\cdot$ $\dots$ $\cdots$ $\ddots$ $\vdots$ $\colon$ $\mid$ \phantom{} \mathstrut{} Квант., операц. $\forall$ $\exists$ $\exists!$ $\nexists$ $\lnot$ $\land$ $\lor$ $\cup$ $\cap$ $\sqcup$ $\sqcap$ $\setminus$ $\bigtriangleup$ $\uplus$ $\cdot$ $\circ$ $\times$ $\pm$ $\mp$ $\dotplus$ $\div$ $/$ $\neg$ $\wedge$ $\vee$ $\barwedge$ $\veebar$ $\curlywedge$ $\curlyvee$ $\textasciicircum$ $\oplus$ $\ominus$ $\otimes$ $\oslash$ $\odot$ $\circledcirc$ $\circledast$ Отношения $\in$ $\notin$ $\ni$ $\not\ni$ $\subset$ $\supset$ $\not\subset$ $\not\supset$ $\subseteq$ $\supseteq$ $\nsubseteq$ $\nsupseteq$ $\subsetneq$ $\supsetneq$ $\subsetneqq$ $\supsetneqq$ $\neq$ $\approx$ $\equiv$ $\not\equiv$ $\sim$ $\nsim$ $\cong$ $\ncong$ $\leqslant$ $\geqslant$ $\nleqslant$ $\ngeqslant$ $\le$ $\ge$ $\nleq$ $\ngeq$ $\nless$ $\ngtr$ $\lneq$ $\gneq$ $\lneqq$ $\gneqq$ $\ll$ $\gg$ $\prec$ $\succ$ $\nprec$ $\nsucc$ $\preceq$ $\succeq$ $\npreceq$ $\nsucceq$ $:=$ $\overset{\mathrm{def}}{=}$ $\triangleq$ $\models$ $\vdash$ $\dashv$ $\mid$ $\nmid$ $\mathop{\vdots}$ $\mathop{\not\vdots}$ $\parallel$ $\nparallel$ $\perp$ $\not\perp$ Большие операт. $\sum_{}^{}$ $\sum_{}$ $\prod_{}^{}$ $\prod_{}$ $\bigcup_{}^{}$ $\bigcup_{}$ $\bigcap_{}^{}$ $\bigcap_{}$ $\bigsqcup_{}^{}$ $\biguplus_{}^{}$ $\bigvee_{}^{}$ $\bigwedge_{}^{}$ $\bigoplus_{}^{}$ $\bigotimes_{}^{}$ $\bigodot_{}^{}$ Стрелки $\to$ $\mapsto$ $\rightarrow$ $\leftarrow$ $\leftrightarrow$ $\nrightarrow$ $\nleftarrow$ $\nleftrightarrow$ $\Rightarrow$ $\Leftarrow$ $\Leftrightarrow$ $\nRightarrow$ $\nLeftarrow$ $\nLeftrightarrow$ $\Uparrow$ $\Downarrow$ $\Updownarrow$ $\rightrightarrows$ $\longmapsto$ $\longrightarrow$ $\longleftarrow$ $\longleftrightarrow$ $\uparrow$ $\downarrow$ $\updownarrow$ $\Longrightarrow$ $\Longleftarrow$ $\Longleftrightarrow$ $\implies$ $\iff$ $\rightleftarrows$ $\nearrow$ $\swarrow$ $\nwarrow$ $\searrow$ $\circlearrowleft$ $\circlearrowright$ $\curvearrowleft$ $\curvearrowright$ $\xrightarrow[]{}$ $\xleftarrow[]{}$ Буквы, значки Греческие $\Gamma$ $\Delta$ $\Theta$ $\Lambda$ $\Xi$ $\Pi$ $\Sigma$ $\Upsilon$ $\Phi$ $\Psi$ $\Omega$ $\digamma$ $\alpha$ $\beta$ $\gamma$ $\delta$ $\epsilon$ $\varepsilon$ $\zeta$ $\eta$ $\theta$ $\vartheta$ $\iota$ $\kappa$ $\varkappa$ $\lambda$ $\mu$ $\nu$ $\xi$ $\pi$ $\varpi$ $\rho$ $\varrho$ $\sigma$ $\varsigma$ $\tau$ $\upsilon$ $\phi$ $\varphi$ $\chi$ $\psi$ $\omega$ Резные $\mathbb{A}$ $\mathbb{B}$ $\mathbb{C}$ $\mathbb{D}$ $\mathbb{E}$ $\mathbb{F}$ $\mathbb{G}$ $\mathbb{H}$ $\mathbb{I}$ $\mathbb{J}$ $\mathbb{K}$ $\mathbb{L}$ $\mathbb{M}$ $\mathbb{N}$ $\mathbb{O}$ $\mathbb{P}$ $\mathbb{Q}$ $\mathbb{R}$ $\mathbb{S}$ $\mathbb{T}$ $\mathbb{U}$ $\mathbb{V}$ $\mathbb{W}$ $\mathbb{X}$ $\mathbb{Y}$ $\mathbb{Z}$ Калиграф. $\mathcal{A}$ $\mathcal{B}$ $\mathcal{C}$ $\mathcal{D}$ $\mathcal{E}$ $\mathcal{F}$ $\mathcal{G}$ $\mathcal{H}$ $\mathcal{I}$ $\mathcal{J}$ $\mathcal{K}$ $\mathcal{L}$ $\mathcal{M}$ $\mathcal{N}$ $\mathcal{O}$ $\mathcal{P}$ $\mathcal{Q}$ $\mathcal{R}$ $\mathcal{S}$ $\mathcal{T}$ $\mathcal{U}$ $\mathcal{V}$ $\mathcal{W}$ $\mathcal{X}$ $\mathcal{Y}$ $\mathcal{Z}$ Рукописные $\mathscr{A}$ $\mathscr{B}$ $\mathscr{C}$ $\mathscr{D}$ $\mathscr{E}$ $\mathscr{F}$ $\mathscr{G}$ $\mathscr{H}$ $\mathscr{I}$ $\mathscr{J}$ $\mathscr{K}$ $\mathscr{L}$ $\mathscr{M}$ $\mathscr{N}$ $\mathscr{O}$ $\mathscr{P}$ $\mathscr{Q}$ $\mathscr{R}$ $\mathscr{S}$ $\mathscr{T}$ $\mathscr{U}$ $\mathscr{V}$ $\mathscr{W}$ $\mathscr{X}$ $\mathscr{Y}$ $\mathscr{Z}$ Готические $\mathfrak{A}$ $\mathfrak{B}$ $\mathfrak{C}$ $\mathfrak{D}$ $\mathfrak{E}$ $\mathfrak{F}$ $\mathfrak{G}$ $\mathfrak{H}$ $\mathfrak{I}$ $\mathfrak{J}$ $\mathfrak{K}$ $\mathfrak{L}$ $\mathfrak{M}$ $\mathfrak{N}$ $\mathfrak{O}$ $\mathfrak{P}$ $\mathfrak{Q}$ $\mathfrak{R}$ $\mathfrak{S}$ $\mathfrak{T}$ $\mathfrak{U}$ $\mathfrak{V}$ $\mathfrak{W}$ $\mathfrak{X}$ $\mathfrak{Y}$ $\mathfrak{Z}$ $\mathfrak{a}$ $\mathfrak{b}$ $\mathfrak{c}$ $\mathfrak{d}$ $\mathfrak{e}$ $\mathfrak{f}$ $\mathfrak{g}$ $\mathfrak{h}$ $\mathfrak{i}$ $\mathfrak{j}$ $\mathfrak{k}$ $\mathfrak{l}$ $\mathfrak{m}$ $\mathfrak{n}$ $\mathfrak{o}$ $\mathfrak{p}$ $\mathfrak{q}$ $\mathfrak{r}$ $\mathfrak{s}$ $\mathfrak{t}$ $\mathfrak{u}$ $\mathfrak{v}$ $\mathfrak{w}$ $\mathfrak{x}$ $\mathfrak{y}$ $\mathfrak{z}$ Значки $\varnothing$ $\infty$ $\partial$ $\aleph$ $\mathfrak{c}$ $\ell$ $\hbar$ $\O$ $\bot$ $\top$ $\angle$ $\measuredangle$ $\sphericalangle$ $\frown$ $\smile$ $\vartriangle$ $\triangledown$ $\blacktriangle$ $\blacktriangledown$ $\triangleleft$ $\triangleright$ $\blacktriangleleft$ $\blacktriangleright$ $\triangle$ $\square$ $\blacksquare$ $\bigcirc$ $\star$ $\bigstar$ $\bullet$ $\diamond$ $\textasciicircum$ $\therefore$ $\because$ $\&$ $\%$ $\S$ $\P$ $\backslash$ Функции, операт. Станд. функц. $\max_{}$ $\min_{}$ $\sup_{}$ $\inf_{}$ $\Pr_{}$ $\operatorname{sign}$ $\deg$ $\arg$ $\operatorname{НОД}$ $\operatorname{НОК}$ $\operatorname{Im}$ $\operatorname{Re}$ $\dim$ $\ker$ $\hom$ $\operatorname{diag}$ $\operatorname{rank}$ $\det$ $\operatorname{tr}$ $\operatorname{spec}$ $\mathsf{P}$ $\mathsf{M}$ $\mathsf{D}$ $\Im$ $\Re$ \operatorname{} Элем. функц. $\exp$ $\log_{}$ $\ln$ $\lg$ $\sin$ $\cos$ $\tg$ $\ctg$ $\arcsin$ $\arccos$ $\arctg$ $\arcctg$ $\sh$ $\ch$ $\th$ $\cth$ Пределы $\lim_{n\to\infty}$ $\lim_{x\to }$ $lim_{}$ $\limsup_{n\to\infty}$ $\liminf_{n\to\infty}$ $\varlimsup_{n\to\infty}$ $\varliminf_{n\to\infty}$ $\to$ $\rightrightarrows$ $\infty$ Дифф. опер. $\mathrm{d}$ $\partial$ $\frac{\mathrm{d} }{\mathrm{d} x}$ $\frac{\partial }{\partial x}$ $\frac{\partial^2 }{\partial x^2}$ $\nabla$ $\Delta$ $\operatorname{grad}$ $\operatorname{div}$ $\operatorname{rot}$ Интегралы $\int$ $\int_{}^{}$ $\int\limits_{}^{}$ $\int_{}$ $\int\limits_{}$ $\oint$ $\oint_{}$ $\oint\limits_{}$ $\ointctrclockwise$ $\ointclockwise$ $\iint$ $\iint_{}$ $\iint\limits_{}$ $\oiint$ $\oiint_{}$ $\oiint\limits_{}$ $\varoiint$ $\sqiint$ $\iiint$ $\iiint_{}$ $\iiint\limits_{}$ $\dotsint$ $\dotsint_{}$ $\dotsint\limits_{}$ Сравнения $\equiv$ $\mod{}$ $\pmod{}$ $\pod{}$ Матрицы $\begin{matrix} & \\ & \end{matrix}$ $\begin{pmatrix} & \\ & \end{pmatrix}$ $\begin{vmatrix} & \\ & \end{vmatrix}$ $\begin{Vmatrix} & \\ & \end{Vmatrix}$ $\begin{bmatrix} & \\ & \end{bmatrix}$ $\begin{Bmatrix} & \\ & \end{Bmatrix}$ $\left\{\begin{matrix} & \\ & \end{matrix}\right.$ $\left[\begin{matrix} & \\ & \end{matrix}\right.$ $\left.\begin{matrix} & \\ & \end{matrix}\right\}$ $\left.\begin{matrix} & \\ & \end{matrix}\right\|$ $\left(\begin{smallmatrix} & \\ & \end{smallmatrix}\right)$ $\binom{}{}$ $\tbinom{}{}$ Спец. блоки $\begin{cases} & \\ & \end{cases}$ $\begin{aligned} & \\ & \end{aligned}$ $\begin{align} & \tag{} \\ & \tag{} \end{align}$ $\begin{tikzpicture} \end{tikzpicture}$ $\ce{}$
Преобразовать url в ссылки Преобразовать $ в tex
* Сколько символов на картинке?
Отправляя данные, вы соглашаетесь с Правилами сайта.

Теги: #математика #задача #фракталы #размерность #дробная_размерность

∀ x, y, z

Разные размерности