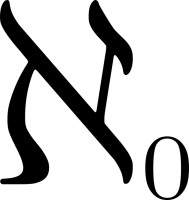В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе не очевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.

Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.

Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде . Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы .


Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

.

Возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.

В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).

Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.

Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.


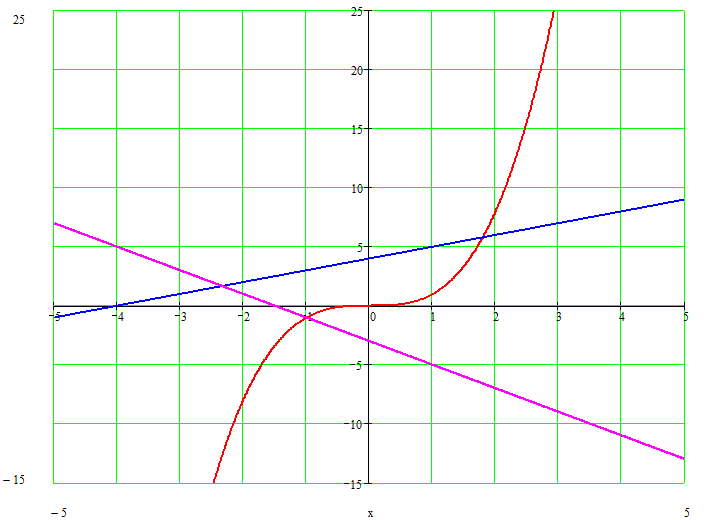
Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. То есть, уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение. Найти его можно воспользовавшись формулой Кардано:

, где .

Немного громоздко, но пока, вроде бы, все в порядке. Или нет?

Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.

Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс. Возьмем классический пример, который рассматривал еще Бомбелли:

.

Внезапно и по формуле . Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.

Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.

Используя подобный подход, Бомбелли установил, в частности, что

,
.

Давайте проверим:



Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.

В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.

Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.

Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.

Ahiin