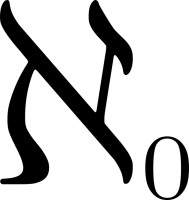Найдите общее решение линейной системы в зависимости от значения параметра лямбда

Сообщения: 2 🔎

# 12 Мар 2016 11:10:39
Math

Найдите общее решение линейной системы в зависимости от значения параметра $\lambda$ . При каких значениях $\lambda$ система допускает решение с помощью обратной матрицы?

$\left\{\begin{matrix} 3x_1 + (\lambda+8)x_2 + (5\lambda+8)x_3 = \lambda + 13 \\ x_1 + (\lambda+4)x_2 + (2\lambda+3)x_3 = \lambda + 6 \\ 2x_1 + (\lambda+6)x_2 + (4\lambda+6)x_3 = \lambda + 10 \end{matrix}\right.$

Решение

Если обозначить

$A = \begin{pmatrix} 3 & \lambda+8 & 5\lambda+8 \\ 1 & \lambda+4 & 2\lambda+3 \\ 2 & \lambda+6 & 4\lambda+6 \end{pmatrix}$ ,

$X = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$ ,

$B = \begin{pmatrix} \lambda + 13 \\ \lambda + 6 \\ \lambda + 10 \end{pmatrix}$ ,

тогда систему можно записать в виде $AX=B$ .

Определитель $\det A = \begin{vmatrix} 3 & \lambda+8 & 5\lambda+8 \\ 1 & \lambda+4 & 2\lambda+3 \\ 2 & \lambda+6 & 4\lambda+6 \end{vmatrix} = \lambda^2 + 3\lambda + 2$ .

Приравнивая к нулю, найдем, что $\det A = 0$ при $\lambda = -2$ и $\lambda = -1$ .

Если $\lambda \ne -2$ и $\lambda \ne -1$ , то матрица $A$ имеет обратную

$A^{-1} = \begin{pmatrix} \frac{2\lambda+3}{\lambda+1} & \frac{\lambda^2}{\lambda^2+3\lambda+2} & -\frac{3\lambda^2+9\lambda+8}{\lambda^2+3\lambda+2} \\ 0 & \frac{2}{\lambda+2} & -\frac{1}{\lambda+2} \\ -\frac{1}{\lambda+1} & -\frac{1}{\lambda+1} & \frac{2}{\lambda+1} \end{pmatrix}$

и решение имеет вид $X = A^{-1}B$ .

Если аккуратно перемножить и упростить, получим $X = \begin{pmatrix} -\frac{1}{\lambda+1} \\ 1 \\ \frac{1}{\lambda+1} \end{pmatrix}$ .

Случаи $\lambda = -2$ и $\lambda = -1$ рассматриваются отдельно. Нужно просто подставить $\lambda$ и решить как обычную систему линейных уравнений с числовыми коэффициентами без параметров, например, методом гаусса.

Можно не использовать обратную матрицу, а применить метод редукции гаусса к расширенной матрице, учитывая, что $\lambda \ne -2$ и $\lambda \ne -1$ ,

$\begin{pmatrix} 3 & \lambda+8 & 5\lambda+8 & \lambda+13\\ 1 & \lambda+4 & 2\lambda+3 & \lambda+6 \\ 2 & \lambda+6 & 4\lambda+6 & \lambda+10 \end{pmatrix}$

и получить

$\begin{pmatrix} 1 & 0 & 0 & -\frac{1}{\lambda+1} \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & \frac{1}{\lambda+1} \end{pmatrix}$ .

При $\lambda = -2$ расширенная матрица

$\begin{pmatrix} 3 & 6 & -2 & 11 \\ 1 & 2 & -1 & 4 \\ 2 & 4 & -2 & 8 \end{pmatrix}$

редуцируется до

$\begin{pmatrix} 1 & 2 & 0 & 3 \\ 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ .

Следовательно решения имеют вид $x_3 = -1,\ x_1 = 3-2x_2$ , или в матричном виде:

$X = \begin{pmatrix} 3-2x_2 \\ x_2 \\ -1 \end{pmatrix}$ .

При $\lambda = -1$ расширенная матрица

$\begin{pmatrix} 3 & 7 & 3 & 12 \\ 1 & 3 & 1 & 5 \\ 2 & 5 & 2 & 9 \end{pmatrix}$

редуцируется до

$\begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$ .

Следовательно, система не имеет решений.

Цитировать

# 10 Ноя 2024 20:16:34

Сообщение ожидает проверки

Сообщения: 2 🔎


*Имя:
Заголовок:
[tex-clear] [tex-help] [ted] formulas > Формат Шрифт $\mathit{}$ $\mathbf{}$ $\mathrm{}$ $\mathsf{}$ $\mathfrak{}$ $\mathbb{}$ $\mathcal{}$ $\mathscr{}$ Размер $\tiny Aa$ $\scriptsize Aa$ $\footnotesize Aa$ $\small Aa$ $\normalsize Aa$ $\large Aa$ $\Large Aa$ $\LARGE Aa$ $\huge Aa$ $\Huge Aa$ Цвет ${\color{Red} }$ ${\color{DarkRed} }$ ${\color{BrickRed} }$ ${\color{Magenta} }$ ${\color{VioletRed} }$ ${\color{Yellow} }$ ${\color{Orange} }$ ${\color{DarkOrange} }$ ${\color{Brown} }$ ${\color{Sepia} }$ ${\color{Green} }$ ${\color{DarkGreen} }$ ${\color{ForestGreen} }$ ${\color{Teal} }$ ${\color{Emerald} }$ ${\color{Blue} }$ ${\color{DarkBlue} }$ ${\color{RoyalBlue} }$ ${\color{BlueViolet} }$ ${\color{Purple} }$ ${\color{Gray} }$ ${\color{Plum} }$ ${\color{Cyan} }$ Стиль \text{} $\tstyle$ $\dstyle$ Дроби, корни $\frac{}{}$ $\tfrac{}{}$ $\dfrac{}{}$ $\cfrac{}{}$ $\over$ $\atop$ $\sqrt{}$ $\sqrt[]{}$ $\binom{}{}$ $\tbinom{}{}$ Скобки $()$ $\{\}$ $[]$ $\|\|$ $\\|\\|$ $\langle \rangle$ $\left( \right)$ $\left\{ \right\}$ $\left[ \right]$ $\left\| \right\|$ $\left\\| \right\\|$ $\left\langle \right\rangle$ $\left( \right.$ $\left. \right)$ $\left\{ \right.$ $\left. \right\}$ $\left[ \right.;$ $\left. \right]$ $\left\| \right.;$ $\left. \right\|$ Декор., индексы $^{}$ $_{}$ $^{}_{}$ ${}^{}$ ${}_{}$ ${}^{}_{}$ $\leftidx{}{}{}$ $\ltrans{}$ $\vec{}$ $\bar{}$ $\tilde{}$ $\hat{}$ $\dot{}$ $\ddot{}$ $\dddot{}$ $^{\circ}$ $\overset{\circ}{}$ $\overset{\frown}{}$ $\overrightarrow{}$ $\overleftarrow{}$ $\overline{}$ $\underline{}$ $\widetilde{}$ $\widehat{}$ $\overbrace{}^{}$ $\underbrace{}_{}$ $\overset{}{}$ $\underset{}{}$ $\left. \right\|_{}^{}$ $\left. \right\|_{}$ $\not{}$ $\cancel{}$ $\bcancel{}$ $\xcancel{}$ Пробелы, разд. $\!$ $x y$ $\,$ $\;$ $\$ $\quad$ $\qquad$ $\cdot$ $\dots$ $\cdots$ $\ddots$ $\vdots$ $\colon$ $\mid$ \phantom{} \mathstrut{} Квант., операц. $\forall$ $\exists$ $\exists!$ $\nexists$ $\lnot$ $\land$ $\lor$ $\cup$ $\cap$ $\sqcup$ $\sqcap$ $\setminus$ $\bigtriangleup$ $\uplus$ $\cdot$ $\circ$ $\times$ $\pm$ $\mp$ $\dotplus$ $\div$ $/$ $\neg$ $\wedge$ $\vee$ $\barwedge$ $\veebar$ $\curlywedge$ $\curlyvee$ $\textasciicircum$ $\oplus$ $\ominus$ $\otimes$ $\oslash$ $\odot$ $\circledcirc$ $\circledast$ Отношения $\in$ $\notin$ $\ni$ $\not\ni$ $\subset$ $\supset$ $\not\subset$ $\not\supset$ $\subseteq$ $\supseteq$ $\nsubseteq$ $\nsupseteq$ $\subsetneq$ $\supsetneq$ $\subsetneqq$ $\supsetneqq$ $\neq$ $\approx$ $\equiv$ $\not\equiv$ $\sim$ $\nsim$ $\cong$ $\ncong$ $\leqslant$ $\geqslant$ $\nleqslant$ $\ngeqslant$ $\le$ $\ge$ $\nleq$ $\ngeq$ $\nless$ $\ngtr$ $\lneq$ $\gneq$ $\lneqq$ $\gneqq$ $\ll$ $\gg$ $\prec$ $\succ$ $\nprec$ $\nsucc$ $\preceq$ $\succeq$ $\npreceq$ $\nsucceq$ $:=$ $\overset{\mathrm{def}}{=}$ $\triangleq$ $\models$ $\vdash$ $\dashv$ $\mid$ $\nmid$ $\mathop{\vdots}$ $\mathop{\not\vdots}$ $\parallel$ $\nparallel$ $\perp$ $\not\perp$ Большие операт. $\sum_{}^{}$ $\sum_{}$ $\prod_{}^{}$ $\prod_{}$ $\bigcup_{}^{}$ $\bigcup_{}$ $\bigcap_{}^{}$ $\bigcap_{}$ $\bigsqcup_{}^{}$ $\biguplus_{}^{}$ $\bigvee_{}^{}$ $\bigwedge_{}^{}$ $\bigoplus_{}^{}$ $\bigotimes_{}^{}$ $\bigodot_{}^{}$ Стрелки $\to$ $\mapsto$ $\rightarrow$ $\leftarrow$ $\leftrightarrow$ $\nrightarrow$ $\nleftarrow$ $\nleftrightarrow$ $\Rightarrow$ $\Leftarrow$ $\Leftrightarrow$ $\nRightarrow$ $\nLeftarrow$ $\nLeftrightarrow$ $\Uparrow$ $\Downarrow$ $\Updownarrow$ $\rightrightarrows$ $\longmapsto$ $\longrightarrow$ $\longleftarrow$ $\longleftrightarrow$ $\uparrow$ $\downarrow$ $\updownarrow$ $\Longrightarrow$ $\Longleftarrow$ $\Longleftrightarrow$ $\implies$ $\iff$ $\rightleftarrows$ $\nearrow$ $\swarrow$ $\nwarrow$ $\searrow$ $\circlearrowleft$ $\circlearrowright$ $\curvearrowleft$ $\curvearrowright$ $\xrightarrow[]{}$ $\xleftarrow[]{}$ Буквы, значки Греческие $\Gamma$ $\Delta$ $\Theta$ $\Lambda$ $\Xi$ $\Pi$ $\Sigma$ $\Upsilon$ $\Phi$ $\Psi$ $\Omega$ $\digamma$ $\alpha$ $\beta$ $\gamma$ $\delta$ $\epsilon$ $\varepsilon$ $\zeta$ $\eta$ $\theta$ $\vartheta$ $\iota$ $\kappa$ $\varkappa$ $\lambda$ $\mu$ $\nu$ $\xi$ $\pi$ $\varpi$ $\rho$ $\varrho$ $\sigma$ $\varsigma$ $\tau$ $\upsilon$ $\phi$ $\varphi$ $\chi$ $\psi$ $\omega$ Резные $\mathbb{A}$ $\mathbb{B}$ $\mathbb{C}$ $\mathbb{D}$ $\mathbb{E}$ $\mathbb{F}$ $\mathbb{G}$ $\mathbb{H}$ $\mathbb{I}$ $\mathbb{J}$ $\mathbb{K}$ $\mathbb{L}$ $\mathbb{M}$ $\mathbb{N}$ $\mathbb{O}$ $\mathbb{P}$ $\mathbb{Q}$ $\mathbb{R}$ $\mathbb{S}$ $\mathbb{T}$ $\mathbb{U}$ $\mathbb{V}$ $\mathbb{W}$ $\mathbb{X}$ $\mathbb{Y}$ $\mathbb{Z}$ Калиграф. $\mathcal{A}$ $\mathcal{B}$ $\mathcal{C}$ $\mathcal{D}$ $\mathcal{E}$ $\mathcal{F}$ $\mathcal{G}$ $\mathcal{H}$ $\mathcal{I}$ $\mathcal{J}$ $\mathcal{K}$ $\mathcal{L}$ $\mathcal{M}$ $\mathcal{N}$ $\mathcal{O}$ $\mathcal{P}$ $\mathcal{Q}$ $\mathcal{R}$ $\mathcal{S}$ $\mathcal{T}$ $\mathcal{U}$ $\mathcal{V}$ $\mathcal{W}$ $\mathcal{X}$ $\mathcal{Y}$ $\mathcal{Z}$ Рукописные $\mathscr{A}$ $\mathscr{B}$ $\mathscr{C}$ $\mathscr{D}$ $\mathscr{E}$ $\mathscr{F}$ $\mathscr{G}$ $\mathscr{H}$ $\mathscr{I}$ $\mathscr{J}$ $\mathscr{K}$ $\mathscr{L}$ $\mathscr{M}$ $\mathscr{N}$ $\mathscr{O}$ $\mathscr{P}$ $\mathscr{Q}$ $\mathscr{R}$ $\mathscr{S}$ $\mathscr{T}$ $\mathscr{U}$ $\mathscr{V}$ $\mathscr{W}$ $\mathscr{X}$ $\mathscr{Y}$ $\mathscr{Z}$ Готические $\mathfrak{A}$ $\mathfrak{B}$ $\mathfrak{C}$ $\mathfrak{D}$ $\mathfrak{E}$ $\mathfrak{F}$ $\mathfrak{G}$ $\mathfrak{H}$ $\mathfrak{I}$ $\mathfrak{J}$ $\mathfrak{K}$ $\mathfrak{L}$ $\mathfrak{M}$ $\mathfrak{N}$ $\mathfrak{O}$ $\mathfrak{P}$ $\mathfrak{Q}$ $\mathfrak{R}$ $\mathfrak{S}$ $\mathfrak{T}$ $\mathfrak{U}$ $\mathfrak{V}$ $\mathfrak{W}$ $\mathfrak{X}$ $\mathfrak{Y}$ $\mathfrak{Z}$ $\mathfrak{a}$ $\mathfrak{b}$ $\mathfrak{c}$ $\mathfrak{d}$ $\mathfrak{e}$ $\mathfrak{f}$ $\mathfrak{g}$ $\mathfrak{h}$ $\mathfrak{i}$ $\mathfrak{j}$ $\mathfrak{k}$ $\mathfrak{l}$ $\mathfrak{m}$ $\mathfrak{n}$ $\mathfrak{o}$ $\mathfrak{p}$ $\mathfrak{q}$ $\mathfrak{r}$ $\mathfrak{s}$ $\mathfrak{t}$ $\mathfrak{u}$ $\mathfrak{v}$ $\mathfrak{w}$ $\mathfrak{x}$ $\mathfrak{y}$ $\mathfrak{z}$ Значки $\varnothing$ $\infty$ $\partial$ $\aleph$ $\mathfrak{c}$ $\ell$ $\hbar$ $\O$ $\bot$ $\top$ $\angle$ $\measuredangle$ $\sphericalangle$ $\frown$ $\smile$ $\vartriangle$ $\triangledown$ $\blacktriangle$ $\blacktriangledown$ $\triangleleft$ $\triangleright$ $\blacktriangleleft$ $\blacktriangleright$ $\triangle$ $\square$ $\blacksquare$ $\bigcirc$ $\star$ $\bigstar$ $\bullet$ $\diamond$ $\textasciicircum$ $\therefore$ $\because$ $\&$ $\%$ $\S$ $\P$ $\backslash$ Функции, операт. Станд. функц. $\max_{}$ $\min_{}$ $\sup_{}$ $\inf_{}$ $\Pr_{}$ $\operatorname{sign}$ $\deg$ $\arg$ $\operatorname{НОД}$ $\operatorname{НОК}$ $\operatorname{Im}$ $\operatorname{Re}$ $\dim$ $\ker$ $\hom$ $\operatorname{diag}$ $\operatorname{rank}$ $\det$ $\operatorname{tr}$ $\operatorname{spec}$ $\mathsf{P}$ $\mathsf{M}$ $\mathsf{D}$ $\Im$ $\Re$ \operatorname{} Элем. функц. $\exp$ $\log_{}$ $\ln$ $\lg$ $\sin$ $\cos$ $\tg$ $\ctg$ $\arcsin$ $\arccos$ $\arctg$ $\arcctg$ $\sh$ $\ch$ $\th$ $\cth$ Пределы $\lim_{n\to\infty}$ $\lim_{x\to }$ $lim_{}$ $\limsup_{n\to\infty}$ $\liminf_{n\to\infty}$ $\varlimsup_{n\to\infty}$ $\varliminf_{n\to\infty}$ $\to$ $\rightrightarrows$ $\infty$ Дифф. опер. $\mathrm{d}$ $\partial$ $\frac{\mathrm{d} }{\mathrm{d} x}$ $\frac{\partial }{\partial x}$ $\frac{\partial^2 }{\partial x^2}$ $\nabla$ $\Delta$ $\operatorname{grad}$ $\operatorname{div}$ $\operatorname{rot}$ Интегралы $\int$ $\int_{}^{}$ $\int\limits_{}^{}$ $\int_{}$ $\int\limits_{}$ $\oint$ $\oint_{}$ $\oint\limits_{}$ $\ointctrclockwise$ $\ointclockwise$ $\iint$ $\iint_{}$ $\iint\limits_{}$ $\oiint$ $\oiint_{}$ $\oiint\limits_{}$ $\varoiint$ $\sqiint$ $\iiint$ $\iiint_{}$ $\iiint\limits_{}$ $\dotsint$ $\dotsint_{}$ $\dotsint\limits_{}$ Сравнения $\equiv$ $\mod{}$ $\pmod{}$ $\pod{}$ Матрицы $\begin{matrix} & \\ & \end{matrix}$ $\begin{pmatrix} & \\ & \end{pmatrix}$ $\begin{vmatrix} & \\ & \end{vmatrix}$ $\begin{Vmatrix} & \\ & \end{Vmatrix}$ $\begin{bmatrix} & \\ & \end{bmatrix}$ $\begin{Bmatrix} & \\ & \end{Bmatrix}$ $\left\{\begin{matrix} & \\ & \end{matrix}\right.$ $\left[\begin{matrix} & \\ & \end{matrix}\right.$ $\left.\begin{matrix} & \\ & \end{matrix}\right\}$ $\left.\begin{matrix} & \\ & \end{matrix}\right\|$ $\left(\begin{smallmatrix} & \\ & \end{smallmatrix}\right)$ $\binom{}{}$ $\tbinom{}{}$ Спец. блоки $\begin{cases} & \\ & \end{cases}$ $\begin{aligned} & \\ & \end{aligned}$ $\begin{align} & \tag{} \\ & \tag{} \end{align}$ $\begin{tikzpicture} \end{tikzpicture}$ $\ce{}$
Преобразовать url в ссылки Преобразовать $ в tex
* Сколько символов на картинке?
Отправляя данные, вы соглашаетесь с Правилами сайта.

∀ x, y, z

Найдите общее решение линейной системы в зависимости от значения параметра лямбда