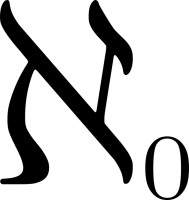Раскрыли все скобки. Сколько слагаемых получилось?

Сообщения: 5 🔎

# 21 Сен 2015 11:07:31
Math

В выражении раскрыли все скобки и привели подобные слагаемые. Сколько слагаемых получилось?

$(1+x)(1+x^2)(1+x^3)\cdots(1+x^{1000})$ ;
$(1+x)(1+x^2)(1+x^3)\cdots(1+x^{13})(1+x^{14})(1+x^{1000})^{18}$ ;
$(1+x^2)^{100}(1+x^3)^{100}$ .

# 26 Сен 2015 01:34:06
WeirdStranger

а) Будем перемножать скобки как обычно: крайнюю левую на следующую, и результатом, соответственно, будет опять крайняя левая скобка. При перемножении крайняя левая скобка всегда будет содержать сумму слагаемых вида $L*x^k, k=\overline {0,n}$ , потому что при умножении, во-первых, содержимое крайней левой скобки дублируется в результирующую (т.к. умножается на $1$ из следующей скобки), и, во-вторых, степени вторых слагаемых в скобках возрастают с шагом $1$ , поэтому и степени в результирующей скобке также будут отличаться на единицу.
В общем виде очередное перемножение скобок выглядит так (Замечание: коэффициенты при степенях далее в решениях указываться не будут, ибо подобные слагаемые по условию уже приведены, соответственно, никакого влияния коэффициенты на количество слагаемых иметь не будут ): $(1+x+x^2+\cdots+x^n)*(1+x^k)$ . Перемножая, получим: $(\underbrace{1+x+x^2+\cdots+x^n}_{\text{Дубликат крайней левой скобки}}+x^k+x^{k+1}+\cdots+x^{n+k})$ . Очевидно, что после приведения подобных слагаемых (а оно понадобится, т.к. при $n>3$ : $1<k<n$ ), учитывая последовательное возрастание степеней с шагом 1, в скобке будет находится $n+k+1$ слагаемых. (Единичка прибавляется, чтобы учесть слагаемое $x^0=1$ ). Следующее перемножение будет иметь вид $(1+x+x^2+\cdots+x^{n+k})*(1+x^{k+1})$ , и в результирующей скобке получим уже $(n+k)+(k+1)+1$ слагаемых и т.д. Учитывая то, что для первой скобки в нашем примере $n=1$ и последняя степень равна $1000$ , получаем количество слагаемых: $1+\sum_{k=1}^{1000}k=1+\frac{1000*(1000+1)}{2}={\color{red}500501}$

б) Найдем количество слагаемых в результате перемножения первых 14-ти скобок по вышевыведенной формуле: $1+\sum_{k=1}^{14}k=1+\frac{14*(14+1)}{2}=106$ . Обозначим результат $(1)$ .
Рассмотрим $(1+x^{1000})^{18}$ : при перемножении первых двух скобок получим $(1+x^{1000}+x^{1000000})*(1+x^{1000})^{16}$ , при перемножении первых трех получим $(1+x^{1000}+x^{1000000}+x^{1000000000})*(1+x^{1000})^{15}$ и т.д. Нетрудно догадаться, что при перемножении $n$ скобок такого вида, мы получим $n+1$ различных слагаемых. Таким образом, результат $(1+x^{1000})^{18}$ будет иметь 19 слагаемых Обозначим результат $(2)$ .
Так как максимальная степень слагаемого в выражении $(1)$ равна $105$ , а степени в выражении $(2)$ начинаются с $0$ и идут дальше с шагом $1000$ , то при умножении выражения $(1)$ на выражение $(2)$ подобных слагаемых не появится, поэтому количество слагаемых в итоговом результате будет $106*19={\color{red}2014}$

в) По вышеприведенным рассуждениям можно легко узнать количество слагаемых в каждой скобке: $\underbrace{(1+x^2+x^4+x^6+\cdots+x^{198}+x^{200})}_{\text{101 слагаемое}}*\underbrace{(1+x^3+x^6+x^9+\cdots+x^{297}+x^{300})}_{\text{101 слагаемое}}$ .
Начнем умножать первую скобку последовательно на каждый из слагаемых второй скобки для выявления зависимости:
1) При умножении первой скобки на $1$ , первая скобка продублируется;
2) При дальнейшем умножении первой скобки на $x^3$ результат примет вид $(1+x^2+x^3+x^4+x^5+\cdots+x^{198}+x^{199}+x^{200}+x^{201}+x^{203})$ . Заметим, что слагаемое $x^{202}$ отсутствует, т.к. его нельзя было получить умножением содержимого первой скобки на $x^3$ . По сути, мы имеем сумму слагаемых вида $x^k, k=\overline {0,203}$ за исключением слагаемого $x^{202}$ (Всего - 203 слагаемых).
3) При дальнейшем умножении первой скобки на $x^6$ в результат добавятся новые слагаемые $x^{202}, x^{204} и x^{206}$ . Результат - сумма слагаемых вида $x^k, k=\overline {0,206}$ за исключением слагаемого $x^{205}$ (Всего - 205 слагаемых);
4) При дальнейшем умножении первой скобки на $x^9$ в результат добавятся новые слагаемые $x^{205}, x^{207} и x^{209}$ . Результат - сумма слагаемых вида $x^k, k=\overline {0,209}$ за исключением слагаемого $x^{208}$ (Всего - 208 слагаемых);

Таким образом, несложно догадаться, что последнее слагаемое итогового результата будет $x^{200+300}=x^{500}$ , слагаемого $x^{499}$ там не будет, ибо для этого нужно $x^{196}$ умножить на $x^{303}$ , которого в скобках у нас, увы, нет, но при этом опять появился бы пробел в последовательности слагаемых от $x^{0}$ до $x^{503}$ в виде отсутствия $x^{502}$ ... Поэтому итоговый результат будет содержать ровно $501-1={\color{red}500}$ слагаемых.

Если заметили какую-либо ошибку - пишите.

Цитировать

# 27 Сен 2015 02:12:36
WeirdStranger

В задаче под буквой в): не учел, что в итоговом результате также отсутствует слагаемое $x^{1}$ , поэтому итоговый результат будет содержать ${\color{red}499}$ слагаемых.

Цитировать

# 27 Сен 2015 16:28:09
Evgeniy

WeirdStranger, не сочтите за поучение, просто хотел посоветовать, вместо $*$ можно ставить точку \cdot. Например $1000 \cdot (1000+1)$ .

Цитировать

# 27 Сен 2015 21:11:16
WeirdStranger

Ага, учту.

Цитировать

Сообщения: 5 🔎


*Имя:
Заголовок:
[tex-clear] [tex-help] [ted] formulas > Формат Шрифт $\mathit{}$ $\mathbf{}$ $\mathrm{}$ $\mathsf{}$ $\mathfrak{}$ $\mathbb{}$ $\mathcal{}$ $\mathscr{}$ Размер $\tiny Aa$ $\scriptsize Aa$ $\footnotesize Aa$ $\small Aa$ $\normalsize Aa$ $\large Aa$ $\Large Aa$ $\LARGE Aa$ $\huge Aa$ $\Huge Aa$ Цвет ${\color{Red} }$ ${\color{DarkRed} }$ ${\color{BrickRed} }$ ${\color{Magenta} }$ ${\color{VioletRed} }$ ${\color{Yellow} }$ ${\color{Orange} }$ ${\color{DarkOrange} }$ ${\color{Brown} }$ ${\color{Sepia} }$ ${\color{Green} }$ ${\color{DarkGreen} }$ ${\color{ForestGreen} }$ ${\color{Teal} }$ ${\color{Emerald} }$ ${\color{Blue} }$ ${\color{DarkBlue} }$ ${\color{RoyalBlue} }$ ${\color{BlueViolet} }$ ${\color{Purple} }$ ${\color{Gray} }$ ${\color{Plum} }$ ${\color{Cyan} }$ Стиль \text{} $\tstyle$ $\dstyle$ Дроби, корни $\frac{}{}$ $\tfrac{}{}$ $\dfrac{}{}$ $\cfrac{}{}$ $\over$ $\atop$ $\sqrt{}$ $\sqrt[]{}$ $\binom{}{}$ $\tbinom{}{}$ Скобки $()$ $\{\}$ $[]$ $\|\|$ $\\|\\|$ $\langle \rangle$ $\left( \right)$ $\left\{ \right\}$ $\left[ \right]$ $\left\| \right\|$ $\left\\| \right\\|$ $\left\langle \right\rangle$ $\left( \right.$ $\left. \right)$ $\left\{ \right.$ $\left. \right\}$ $\left[ \right.;$ $\left. \right]$ $\left\| \right.;$ $\left. \right\|$ Декор., индексы $^{}$ $_{}$ $^{}_{}$ ${}^{}$ ${}_{}$ ${}^{}_{}$ $\leftidx{}{}{}$ $\ltrans{}$ $\vec{}$ $\bar{}$ $\tilde{}$ $\hat{}$ $\dot{}$ $\ddot{}$ $\dddot{}$ $^{\circ}$ $\overset{\circ}{}$ $\overset{\frown}{}$ $\overrightarrow{}$ $\overleftarrow{}$ $\overline{}$ $\underline{}$ $\widetilde{}$ $\widehat{}$ $\overbrace{}^{}$ $\underbrace{}_{}$ $\overset{}{}$ $\underset{}{}$ $\left. \right\|_{}^{}$ $\left. \right\|_{}$ $\not{}$ $\cancel{}$ $\bcancel{}$ $\xcancel{}$ Пробелы, разд. $\!$ $x y$ $\,$ $\;$ $\$ $\quad$ $\qquad$ $\cdot$ $\dots$ $\cdots$ $\ddots$ $\vdots$ $\colon$ $\mid$ \phantom{} \mathstrut{} Квант., операц. $\forall$ $\exists$ $\exists!$ $\nexists$ $\lnot$ $\land$ $\lor$ $\cup$ $\cap$ $\sqcup$ $\sqcap$ $\setminus$ $\bigtriangleup$ $\uplus$ $\cdot$ $\circ$ $\times$ $\pm$ $\mp$ $\dotplus$ $\div$ $/$ $\neg$ $\wedge$ $\vee$ $\barwedge$ $\veebar$ $\curlywedge$ $\curlyvee$ $\textasciicircum$ $\oplus$ $\ominus$ $\otimes$ $\oslash$ $\odot$ $\circledcirc$ $\circledast$ Отношения $\in$ $\notin$ $\ni$ $\not\ni$ $\subset$ $\supset$ $\not\subset$ $\not\supset$ $\subseteq$ $\supseteq$ $\nsubseteq$ $\nsupseteq$ $\subsetneq$ $\supsetneq$ $\subsetneqq$ $\supsetneqq$ $\neq$ $\approx$ $\equiv$ $\not\equiv$ $\sim$ $\nsim$ $\cong$ $\ncong$ $\leqslant$ $\geqslant$ $\nleqslant$ $\ngeqslant$ $\le$ $\ge$ $\nleq$ $\ngeq$ $\nless$ $\ngtr$ $\lneq$ $\gneq$ $\lneqq$ $\gneqq$ $\ll$ $\gg$ $\prec$ $\succ$ $\nprec$ $\nsucc$ $\preceq$ $\succeq$ $\npreceq$ $\nsucceq$ $:=$ $\overset{\mathrm{def}}{=}$ $\triangleq$ $\models$ $\vdash$ $\dashv$ $\mid$ $\nmid$ $\mathop{\vdots}$ $\mathop{\not\vdots}$ $\parallel$ $\nparallel$ $\perp$ $\not\perp$ Большие операт. $\sum_{}^{}$ $\sum_{}$ $\prod_{}^{}$ $\prod_{}$ $\bigcup_{}^{}$ $\bigcup_{}$ $\bigcap_{}^{}$ $\bigcap_{}$ $\bigsqcup_{}^{}$ $\biguplus_{}^{}$ $\bigvee_{}^{}$ $\bigwedge_{}^{}$ $\bigoplus_{}^{}$ $\bigotimes_{}^{}$ $\bigodot_{}^{}$ Стрелки $\to$ $\mapsto$ $\rightarrow$ $\leftarrow$ $\leftrightarrow$ $\nrightarrow$ $\nleftarrow$ $\nleftrightarrow$ $\Rightarrow$ $\Leftarrow$ $\Leftrightarrow$ $\nRightarrow$ $\nLeftarrow$ $\nLeftrightarrow$ $\Uparrow$ $\Downarrow$ $\Updownarrow$ $\rightrightarrows$ $\longmapsto$ $\longrightarrow$ $\longleftarrow$ $\longleftrightarrow$ $\uparrow$ $\downarrow$ $\updownarrow$ $\Longrightarrow$ $\Longleftarrow$ $\Longleftrightarrow$ $\implies$ $\iff$ $\rightleftarrows$ $\nearrow$ $\swarrow$ $\nwarrow$ $\searrow$ $\circlearrowleft$ $\circlearrowright$ $\curvearrowleft$ $\curvearrowright$ $\xrightarrow[]{}$ $\xleftarrow[]{}$ Буквы, значки Греческие $\Gamma$ $\Delta$ $\Theta$ $\Lambda$ $\Xi$ $\Pi$ $\Sigma$ $\Upsilon$ $\Phi$ $\Psi$ $\Omega$ $\digamma$ $\alpha$ $\beta$ $\gamma$ $\delta$ $\epsilon$ $\varepsilon$ $\zeta$ $\eta$ $\theta$ $\vartheta$ $\iota$ $\kappa$ $\varkappa$ $\lambda$ $\mu$ $\nu$ $\xi$ $\pi$ $\varpi$ $\rho$ $\varrho$ $\sigma$ $\varsigma$ $\tau$ $\upsilon$ $\phi$ $\varphi$ $\chi$ $\psi$ $\omega$ Резные $\mathbb{A}$ $\mathbb{B}$ $\mathbb{C}$ $\mathbb{D}$ $\mathbb{E}$ $\mathbb{F}$ $\mathbb{G}$ $\mathbb{H}$ $\mathbb{I}$ $\mathbb{J}$ $\mathbb{K}$ $\mathbb{L}$ $\mathbb{M}$ $\mathbb{N}$ $\mathbb{O}$ $\mathbb{P}$ $\mathbb{Q}$ $\mathbb{R}$ $\mathbb{S}$ $\mathbb{T}$ $\mathbb{U}$ $\mathbb{V}$ $\mathbb{W}$ $\mathbb{X}$ $\mathbb{Y}$ $\mathbb{Z}$ Калиграф. $\mathcal{A}$ $\mathcal{B}$ $\mathcal{C}$ $\mathcal{D}$ $\mathcal{E}$ $\mathcal{F}$ $\mathcal{G}$ $\mathcal{H}$ $\mathcal{I}$ $\mathcal{J}$ $\mathcal{K}$ $\mathcal{L}$ $\mathcal{M}$ $\mathcal{N}$ $\mathcal{O}$ $\mathcal{P}$ $\mathcal{Q}$ $\mathcal{R}$ $\mathcal{S}$ $\mathcal{T}$ $\mathcal{U}$ $\mathcal{V}$ $\mathcal{W}$ $\mathcal{X}$ $\mathcal{Y}$ $\mathcal{Z}$ Рукописные $\mathscr{A}$ $\mathscr{B}$ $\mathscr{C}$ $\mathscr{D}$ $\mathscr{E}$ $\mathscr{F}$ $\mathscr{G}$ $\mathscr{H}$ $\mathscr{I}$ $\mathscr{J}$ $\mathscr{K}$ $\mathscr{L}$ $\mathscr{M}$ $\mathscr{N}$ $\mathscr{O}$ $\mathscr{P}$ $\mathscr{Q}$ $\mathscr{R}$ $\mathscr{S}$ $\mathscr{T}$ $\mathscr{U}$ $\mathscr{V}$ $\mathscr{W}$ $\mathscr{X}$ $\mathscr{Y}$ $\mathscr{Z}$ Готические $\mathfrak{A}$ $\mathfrak{B}$ $\mathfrak{C}$ $\mathfrak{D}$ $\mathfrak{E}$ $\mathfrak{F}$ $\mathfrak{G}$ $\mathfrak{H}$ $\mathfrak{I}$ $\mathfrak{J}$ $\mathfrak{K}$ $\mathfrak{L}$ $\mathfrak{M}$ $\mathfrak{N}$ $\mathfrak{O}$ $\mathfrak{P}$ $\mathfrak{Q}$ $\mathfrak{R}$ $\mathfrak{S}$ $\mathfrak{T}$ $\mathfrak{U}$ $\mathfrak{V}$ $\mathfrak{W}$ $\mathfrak{X}$ $\mathfrak{Y}$ $\mathfrak{Z}$ $\mathfrak{a}$ $\mathfrak{b}$ $\mathfrak{c}$ $\mathfrak{d}$ $\mathfrak{e}$ $\mathfrak{f}$ $\mathfrak{g}$ $\mathfrak{h}$ $\mathfrak{i}$ $\mathfrak{j}$ $\mathfrak{k}$ $\mathfrak{l}$ $\mathfrak{m}$ $\mathfrak{n}$ $\mathfrak{o}$ $\mathfrak{p}$ $\mathfrak{q}$ $\mathfrak{r}$ $\mathfrak{s}$ $\mathfrak{t}$ $\mathfrak{u}$ $\mathfrak{v}$ $\mathfrak{w}$ $\mathfrak{x}$ $\mathfrak{y}$ $\mathfrak{z}$ Значки $\varnothing$ $\infty$ $\partial$ $\aleph$ $\mathfrak{c}$ $\ell$ $\hbar$ $\O$ $\bot$ $\top$ $\angle$ $\measuredangle$ $\sphericalangle$ $\frown$ $\smile$ $\vartriangle$ $\triangledown$ $\blacktriangle$ $\blacktriangledown$ $\triangleleft$ $\triangleright$ $\blacktriangleleft$ $\blacktriangleright$ $\triangle$ $\square$ $\blacksquare$ $\bigcirc$ $\star$ $\bigstar$ $\bullet$ $\diamond$ $\textasciicircum$ $\therefore$ $\because$ $\&$ $\%$ $\S$ $\P$ $\backslash$ Функции, операт. Станд. функц. $\max_{}$ $\min_{}$ $\sup_{}$ $\inf_{}$ $\Pr_{}$ $\operatorname{sign}$ $\deg$ $\arg$ $\operatorname{НОД}$ $\operatorname{НОК}$ $\operatorname{Im}$ $\operatorname{Re}$ $\dim$ $\ker$ $\hom$ $\operatorname{diag}$ $\operatorname{rank}$ $\det$ $\operatorname{tr}$ $\operatorname{spec}$ $\mathsf{P}$ $\mathsf{M}$ $\mathsf{D}$ $\Im$ $\Re$ \operatorname{} Элем. функц. $\exp$ $\log_{}$ $\ln$ $\lg$ $\sin$ $\cos$ $\tg$ $\ctg$ $\arcsin$ $\arccos$ $\arctg$ $\arcctg$ $\sh$ $\ch$ $\th$ $\cth$ Пределы $\lim_{n\to\infty}$ $\lim_{x\to }$ $lim_{}$ $\limsup_{n\to\infty}$ $\liminf_{n\to\infty}$ $\varlimsup_{n\to\infty}$ $\varliminf_{n\to\infty}$ $\to$ $\rightrightarrows$ $\infty$ Дифф. опер. $\mathrm{d}$ $\partial$ $\frac{\mathrm{d} }{\mathrm{d} x}$ $\frac{\partial }{\partial x}$ $\frac{\partial^2 }{\partial x^2}$ $\nabla$ $\Delta$ $\operatorname{grad}$ $\operatorname{div}$ $\operatorname{rot}$ Интегралы $\int$ $\int_{}^{}$ $\int\limits_{}^{}$ $\int_{}$ $\int\limits_{}$ $\oint$ $\oint_{}$ $\oint\limits_{}$ $\ointctrclockwise$ $\ointclockwise$ $\iint$ $\iint_{}$ $\iint\limits_{}$ $\oiint$ $\oiint_{}$ $\oiint\limits_{}$ $\varoiint$ $\sqiint$ $\iiint$ $\iiint_{}$ $\iiint\limits_{}$ $\dotsint$ $\dotsint_{}$ $\dotsint\limits_{}$ Сравнения $\equiv$ $\mod{}$ $\pmod{}$ $\pod{}$ Матрицы $\begin{matrix} & \\ & \end{matrix}$ $\begin{pmatrix} & \\ & \end{pmatrix}$ $\begin{vmatrix} & \\ & \end{vmatrix}$ $\begin{Vmatrix} & \\ & \end{Vmatrix}$ $\begin{bmatrix} & \\ & \end{bmatrix}$ $\begin{Bmatrix} & \\ & \end{Bmatrix}$ $\left\{\begin{matrix} & \\ & \end{matrix}\right.$ $\left[\begin{matrix} & \\ & \end{matrix}\right.$ $\left.\begin{matrix} & \\ & \end{matrix}\right\}$ $\left.\begin{matrix} & \\ & \end{matrix}\right\|$ $\left(\begin{smallmatrix} & \\ & \end{smallmatrix}\right)$ $\binom{}{}$ $\tbinom{}{}$ Спец. блоки $\begin{cases} & \\ & \end{cases}$ $\begin{aligned} & \\ & \end{aligned}$ $\begin{align} & \tag{} \\ & \tag{} \end{align}$ $\begin{tikzpicture} \end{tikzpicture}$ $\ce{}$
Преобразовать url в ссылки Преобразовать $ в tex
* Сколько символов на картинке?
Отправляя данные, вы соглашаетесь с Правилами сайта.

∀ x, y, z

Раскрыли все скобки. Сколько слагаемых получилось?