|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Соотношение де Бройля |
Соотношение де Бройля
Длина волны квантовой частицы обратно пропорциональна ее импульсу.
Один из фактов субатомного мира заключается в том, что его объекты — такие как электроны или фотоны — совсем не похожи на привычные объекты макромира. Они ведут себя и не как частицы, и не как волны, а как совершенно особые образования, проявляющие и волновые, и корпускулярные свойства в зависимости от обстоятельств (см. Принцип дополнительности). Одно дело — это заявить, и совсем другое — связать воедино волновые и корпускулярные аспекты поведения квантовых частиц, описав их точным уравнением. Именно это и было сделано в соотношении де Бройля. Луи де Бройль опубликовал выведенное им соотношение в качестве составной части своей докторской диссертации в 1924 году. Казавшееся сначала сумасшедшей идей, соотношение де Бройля в корне перевернуло представления физиков-теоретиков о микромире и сыграло важнейшую роль в становлении квантовой механики. В дальнейшем карьера де Бройля сложилась весьма прозаично: до выхода на пенсию он работал профессором физики в Париже и никогда более не поднимался до головокружительных высот революционных прозрений. Теперь кратко опишем физический смысл соотношения де Бройля: одна из физических характеристик любой частицы — ее скорость. При этом физики по ряду теоретических и практических соображений предпочитают говорить не о скорости частицы как таковой, а о ее импульсе (или количестве движения), который равен произведению скорости частицы на ее массу. Волна описывается совсем другими фундаментальными характеристиками — длиной (расстоянием между двумя соседними пиками амплитуды одного знака) или частотой (величина, обратно пропорциональная длине волны, то есть число пиков, проходящих через фиксированную точку за единицу времени). Де Бройлю же удалось сформулировать соотношение, связывающее импульс квантовой частицы Это соотношение гласит буквально следующее: при желании можно рассматривать квантовый объект как частицу, обладающую количеством движения Соотношение де Бройля позволило объяснить одну из величайших загадок зарождающейся квантовой механики. Когда Нильс Бор предложил свою модель атома, она включала концепцию разрешенных орбит электронов вокруг ядра, по которым они могли сколь угодно долго вращаться без потери энергии. С помощью соотношения де Бройля мы можем проиллюстрировать это понятие. Если считать электрон частицей, то, чтобы электрон оставался на своей орбите, у него должна быть одна и та же скорость (или, вернее, импульс) на любом расстоянии от ядра. Если же считать электрон волной, то, чтобы он вписался в орбиту заданного радиуса, надо, чтобы длина окружности этой орбиты была равна целому числу длины его волны. Иными словами, окружность орбиты электрона может равняться только одной, двум, трем (и так далее) длинам его волн. В случае нецелого числа длин волны электрон просто не попадет на нужную орбиту. Главный же физический смысл соотношения де Бройля в том, что мы всегда можем определить разрешенные импульсы (в корпускулярном представлении) или длины волн (в волновом представлении) электронов на орбитах. Для большинства орбит, однако, соотношение де Бройля показывает, что электрон (рассматриваемый как частица) с конкретным импульсом не может иметь соответствующую длину волны (в волновом представлении) такую, что он впишется в эту орбиту. И наоборот, электрон, рассматриваемый как волна определенной длины, далеко не всегда будет иметь соответствующий импульс, который позволит электрону оставаться на орбите (в корпускулярном представлении). Иными словами, для большинства орбит с конкретным радиусом либо волновое, либо корпускулярное описание покажет, что электрон не может находиться на этом расстоянии от ядра. Однако существует небольшое количество орбит, на которых волновое и корпускулярное представление об электроне совпадают. Для этих орбит импульс, необходимый для того, чтобы электрон продолжал движение по орбите (корпускулярное описание), в точности соответствует длине волны, необходимой, чтобы электрон вписался в окружность (волновое описание). Именно эти орбиты и оказываются разрешенными в модели атома Бора, поскольку только на них корпускулярные и волновые свойства электронов не вступают в противоречие. Мне нравится еще одна интерпретация этого принципа — философская: модель атома Бора допускает только такие состояния и орбиты электронов, при которых не важно, какую из двух ментальных категорий человек применяет для их описания. То есть, иными словами, реальный микромир устроен так, что ему нет дела до того, в каких категориях мы пытаемся его осмыслить! Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания». Джеймс Трефил — профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Соотношение де Бройля |
|
[time: 8 ms; queries: 7]
22 Фев 2026 08:37:17 GMT+3 |


 Имеется целый ряд типов электромагнитного излучения, начиная с радиоволн и заканчивая гамма-лучами. Электромагнитные лучи всех типов распространяются в вакууме со скоростью света и отличаются друг от друга только длинами волн.
Имеется целый ряд типов электромагнитного излучения, начиная с радиоволн и заканчивая гамма-лучами. Электромагнитные лучи всех типов распространяются в вакууме со скоростью света и отличаются друг от друга только длинами волн. Вам, наверняка, хоть раз в жизни доводилось стоять у дороги, по которой проносится машина со спецсигналом и включенной сиреной. Пока вой сирены приближается, его тон выше, затем, когда машина поравняется с вами, он понижается, и, наконец, когда машина начинает удаляться, он понижается еще, и получается знакомое: ййййииииээээЭААААОоооуууумммм — такой примерно звукоряд. Сами того, возможно, не сознавая, вы при этом наблюдаете фундаментальнейшее (и полезнейшее) свойство волн.
Вам, наверняка, хоть раз в жизни доводилось стоять у дороги, по которой проносится машина со спецсигналом и включенной сиреной. Пока вой сирены приближается, его тон выше, затем, когда машина поравняется с вами, он понижается, и, наконец, когда машина начинает удаляться, он понижается еще, и получается знакомое: ййййииииээээЭААААОоооуууумммм — такой примерно звукоряд. Сами того, возможно, не сознавая, вы при этом наблюдаете фундаментальнейшее (и полезнейшее) свойство волн. Свет — основа жизни на нашей планете. Отвечая на вопросы «Почему небо голубое?» и «Почему трава зеленая?» можно давать однозначный ответ — «Благодаря свету». Эта неотъемлемая часть нашей жизни, но мы все еще стараемся понять феномен света…
Свет — основа жизни на нашей планете. Отвечая на вопросы «Почему небо голубое?» и «Почему трава зеленая?» можно давать однозначный ответ — «Благодаря свету». Эта неотъемлемая часть нашей жизни, но мы все еще стараемся понять феномен света…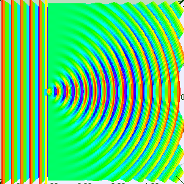 Основы явления дифракции можно понять, если обратиться к принципу Гюйгенса, согласно которому каждая точка на пути распространения светового луча может рассматриваться как новый независимый источник вторичных волн, и дальнейшая дифракционная картина оказывается обусловленной интерференцией этих вторичных волн. При взаимодействии световой волны с препятствием часть вторичных волн Гюйгенса блокируется.
Основы явления дифракции можно понять, если обратиться к принципу Гюйгенса, согласно которому каждая точка на пути распространения светового луча может рассматриваться как новый независимый источник вторичных волн, и дальнейшая дифракционная картина оказывается обусловленной интерференцией этих вторичных волн. При взаимодействии световой волны с препятствием часть вторичных волн Гюйгенса блокируется.