Что изучает физика? Ответ кажется тривиальным. Наука физика изучает природу. Но физики вовсе не изучают природу непосредственно, они не занимаются явлениями природы, как таковыми. Физик наблюдает за стрелками приборов, проводит измерения, но потом что-то пишет на бумаге, делает какие-то вычисления, приходит к каким-то выводам о результатах тех или иных экспериментов.

Прежде чем ставить эксперимент или производить какие-то вычисления, физик создает в своем уме некую модель тех явлений, которые он хочет изучить, исследовать. Анализируя модель, физик делает вывод, какой должен быть результат эксперимента. Он ожидает, что если собрать такой-то прибор, то стрелки будут показывать то-то и то-то. Он собирает такой прибор, ставит эксперимент и убеждается, что стрелки ведут себя нужным образом. Он с удовлетворением говорит, что его модель достаточно точно отражает исследуемое явление. Вот непосредственно чем занимаются физики. Таким образом, основное в деятельности ученых-естествоиспытателей — это исследование не окружающего мира, а его моделей.

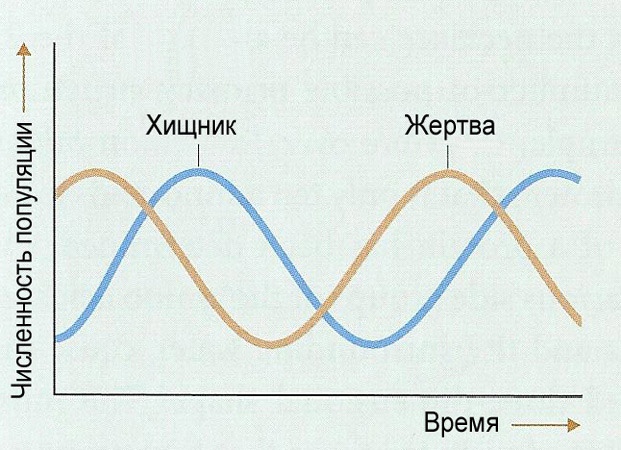
Рассматривая модели в разных науках, мы вдруг обнаруживаем группы чрезвычайно сходных моделей и результаты, полученные в одной модели, могут быть применены в другой. Например, изменение численности хищника в системе хищник — жертва очень похоже на изменение силы тока в колебательном контуре. Схожесть моделей можно по-иному выразить, сказав, что модели каждого класса имеют общую схему, т.е. что схожие модели — это модели, которые основываются на одной и той же схеме.

Введя таким образом понятие схемы, мы приходим к задаче абстрактного изучения схем как таковых, безотносительно к их конкретному воплощению. Математикой называется наука, изучающая все возможные — хотя бы мысленно — схемы, их взаимосвязи, методы их конструирования, иерархии схем (схемы схем) и т.д. и т.п. Иначе говоря, математика есть наука о схемах моделей окружающего мира.

Математики детально изучают имеющиеся схемы моделей и обобщают опыт их применения. Результатом являются некие рецепты, которые и выдаются практикам в виде математических методов исследования (например, чтобы найти объем, надо вычислить интеграл). Предметом преподавания в школе и во втузах и являются в основном эти рецепты. Их применение (скажем, определение оптимальной формы коробки) — это, конечно, не дело математиков, точно так же, как шитье платья по выкройке — не работа модельера.

Однако, многочисленность разнообразных схем моделей, накопленных в математике, не позволяет практику (скажем, инженеру) их все знать. Поэтому вторая задача математиков — помочь практике в создании моделей по еще не получившим широкой известности схемам. С этой целью в математике изучаются не только схемы реальных моделей, но и схемы схем, схемы схем схем и т.д. до бесконечности. На практике это выражается в приобретении опыта конструирования схем на примерах решения головоломных, чисто математических задач. В результате очень часто при ответе на какой-нибудь вопрос из практики математик, как фокусник из рукава, вытаскивает уже готовую схему и вместе с ней решение практической задачи.