Глава 15. Математика шахматных турниров

Среди систем, по которым проводятся шахматные соревнования, наиболее распространены следующие: олимпийская, швейцарская, круговая, матчевая, схевенингенская54, и каждая из них имеет свои математические особенности.

В турнирах, проводимых по олимпийской, или кубковой, системе проигравшие сразу выбывают из борьбы, и поэтому элемент случайности здесь наиболее велик. Такая система хороша для тех, кто любит играть по оринципу «или все, или ничего».

В кубках как бы считается, что если шахматист А играет сильнее Б, а Б, в свою очередь, сильнее В, то и А играет сильнее В, т. е. что отношение между силой шахматистов, как говорят математики, транзитивно. Однако на орактике дело обстоит далеко не так. Например, чемпион мира Ласкер постоянно выигрывал у Чигорина, Чигорин побеждал Пильсбери, а Пильсбери имел перевес в счете с Ласкером. А вот пример аналогичного нарушения транзитивности для современных шахматистов: Фишер имеет оеревес в личных встречах с Ларсеном, Ларсен * - с Геллером, а у Геллера перевес в счете против Фишера. Из сказанного, в частности, следует, какую большую роль в кубке играет жребий…

Если все же считать, что транзитивность имеет место, то возникают интересные математические задачи. Они связаны главным образом с нахождением минимального числа партий, необходимых для определения одного или нескольких победителей кубкового турнира. Вот простейшая задача такого типа55.

В розыгрыше кубка города участвуют n шахматистов. Предварительно проводятся кубки районов, и победители уже разыгрывают главный кубок (противники играют по одной партии, и при ничьей белые выбывают). Сколько партий нужно сыграть, чтобы определить обладателя кубка города, если в нем р районов с числом шахматистов n₁, n₂, …, n_p?

Для решения задачи достаточно заметить, что поело каждой партии из борьбы-выбывает ровно один участник. Так как в конце концов из n шахматистов, разыгрывающих кубок, выбывают (n - 1) - все, кроме победителя, то всего будет сыграна (n - 1) партия. Таким образом, ответ не зависит ни от числа районов в городе, ни от распределения шахматистов в них.

Преимущество олимпийской системы заключается в большом числе шахматистов, которые могут одновременно играть в турнире (точнее, начать его). Тем же достоинством обладает и швейцарская система, которая имеет еще один плюс - проигравшие здесь не выбывают. Эта система обычно применяется в турнирах с числом участников, большим 20. При этом 10 - 13 туров, как правило, хватает, чтобы определить достойных победителей. Напомним, например, что XXXV юбилейный чемпионат страны (Харьков, 1967 г.) проходил по швейцарской системе; в нем играло 130 шахматистов (в 13 туров), и чемпионами стали М. Таль и Л. Полугаевский.

Перед началом турнира по швейцарской системе проводится жеребьевка. В первом туре встречаются номера 1 и 2, 3 и 4 и т. д., причем нечетные номера играют белыми. В последующих турах, опять же по жребию, между собой играют участники, имеющие одинаковое количество очков. Если в одной «очковой» группе число участников нечетно или их не удается разбить на пары так, чтобы партнеры каждой пары встречались впервые, то «смешивают» соседние группы. При жеребьевке стремятся к тому, чтобы участники чередовали цвет фигур.

Самая распространенная и объективная система проведения шахматных соревнований - круговая, при которой все участники турнира встречаются друг с другом. Иногда, чтобы элемент случайности свести к минимуму, турнир проводят в два или даже большее число кругов. Порядок встреч по турам и цвет фигур, которым играют шахматисты в круговом турнире, зависит только от номеров его участников (получаемых ими при жеребьевке) и указывается в специальных таблицах, составленных немецким шахматистом Й. Бергером. Несложный математический анализ этих таблйц позволяет вывести простые правила для нахождение номера тура,, в котором встречаются противники, и цвета их фигур. Укажем эти оравила для турнира с четным числом участников n.

Если номера обоих участников отличны от n, то сложим их. Номер тура получается при вычитании из этой суммы 1, если она не превосходит n, и вычитании n, если она больше n. Если сумма нечетна, то белыми играет меньший номер, а если четна, то - больший. Например, ори десяти участниках второй номер с пятым играет белыми в 6-м туре (2 + 5 = 7 - нечетное число, меньшее 40; 7 - 1 = 6), а шестой номер с восьмым играет черными в 4-м туре (6 + 8 = 14 - четное число, большее 10; 14 - 10 = 4).

Расписание встреч последнего номера отличается от остальных. Чтобы узнать, в каком туре он играет с данным участником, удвоим номер этого участника. Теперь из результата надо вычесть 1, если он не больше n, и вычесть n, если больше. При этом с первой половиной номеров последний участник играет черными, а со второй - белыми.

Если число участников n нечетно, то добавлением «фиктивного» участника с номером n + 1 мы перейдем к уже разобранному случаю. При этом встреча с «фиктивным» партнером попросту означает, что в соответствующем туре шахматист свободен от игры. При четном n участники первой половины турнирной таблицы играют на одну партию белыми больше (за счет «белой» партии с последним номером), и поэтому при жеребьевке шахматисты предпочитают вытягивать номера от 1 до n/2.

По круговой системе проводятся не только шахматные турниры; используют ее и в соревнованиях по другим видам спорта, например по футболу. Но такое математически строгое расписание игр по турам применяется, пожалуй, только в шахматах (и шашках). Это объясняется тем, что шахматные соревнования проходят компактно, в сжатые сроки (конечно, это не касается турниров по переписке, в которых все партии вообще играются одновременно и могут продолжаться не один год). При составлении календаря игр в футбольном чемпионате страны приходится учитывать международные матчи, считаться с погодой, климатом и т. д.

Всякий закончившийся круговой турнир полностью характеризуется графом, вершины которого соответствуют участникам турнира, а ребра - встречам между ними. Такой граф содержит n вершин и C²_n  ребер и называется полным. Если партия результативна, то соответствующему ребру можно приписать стрелку, направленную от победителя к побежденному. Графы такого типа (и их обобщения) называются графами турниров, их исследованию посвящено довольно много серьезных работ.

О круговых турнирах составлено множество математических и логических задач. Конечно, в их формулировке можно использовать различные виды спорта, но предпочтение почти всегда отдается шахматам. Рассмотрим несколько таких задач.

Всего в круговом турнире было сыграно 55 партий. Два участника выбыли из него, один успел сыграть 10 партий, а другой - одну. Встречались ли эти шахматисты между собой?

Пусть n - число участников турнира, тогда (n - 2) шахматиста, закончившие турнир, сыграли между собой (n - 2)(n - 3)/2 партий. А два интересующих нас шахматиста провели 10 или 11 встреч - в зависимости от того, сыграли между собой или нет. Таким образом, надо рассмотреть два квадратных уравнения:

(n - 2)(n - 3)/2 + 10 = 55 и (n - 2)(n - 3)/2 + 11 = 55.

При этом нас интересуют лишь целые и положительные значения n. Такое решение (n = 12) имеет лишь первое уравнение, откуда и следует, что указанная партия состоялась.

Для тренировки шахматист играет не менее одной партии в день и, чтобы не переутомиться, не более 12 партий в неделю. Доказать, что можно найти несколько дней подряд, в течение которых он сыграет ровно 20 партий.

Так как шахматист играет не более 12 партий в неделю, то за 77 дней он проведет не более 132 встреч. Пусть а_i - число партий, сыгранных им за i дней, начиная с первого. Поскольку каждый день играется хотя бы одна партия, то среди чисел а₁, a₂, …, а₇₇ нет равных, причем а₇₇ ≤ 132.

Осталось убедиться, что среди этих чисел найдется хотя бы одна пара таких, разность между которыми равна 20. Если это не так, то среди следующих 153 чисел: а₁, а₂, …, а₇₇, а₁ + 20, …, a₇₆ + 20 также нет равных. Это означает, что а₇₆ + 20 ≥ 153, т. е. а₇₇ > а₇₆ ≥ 133 - противоречие. По существу, мы здесь использовали так называемый принцип Дирихле, утверждающий, что если в каждую клетку сажать не более одного зайца, то разместить шесть зайцев в пяти клетках невозможно.

В турнире играло n шахматистов - гроссмейстеров и мастеров. После его окончания оказалось, что каждый участник половину очков набрал, играя с мастерами. Доказать, что √n - целое число.

Пусть а - число мастеров, а b - гроссмейстеров. Мастера между собой разыграли а(а - 1)/2 очков, а так как это половина всех их очков, то столько же они набрали с гроссмейстерами. Аналогично гроссмейстеры, как между собой, так и с мастерами, набрали b(b - 1)/2 очков. Из того, что число партий между старшим и младшими по званню равно аb, получаем (а - 1)/2 + b(b - 1)/2 = ab или, после упрощений, а + b = (а - b)². Так как n = а + b, то √n = √a + b = |а - b| - целое число, что и требовалось доказать.

Доказать, что по окончании кругового турнира всех его участников можно занумеровать так, чтобы ни один из них не имел поражения от участника со следующим номером.

Воспользуемся методом математической индукции. Для двух участников утверждение очевидно. Предположим теперь, что оно верно для произвольного турнира с к участниками. Покажем, что в этом случае в требуемом порядке можно расположить и k + 1 участников. Расположим нужным образом произвольных k из них (по предположению это можно сделать) и посмотрим, как (k + 1)-й сыграл с первым. Если он выиграл или сыграл вничью, то поставим его на первое место, а если проиграл, то посмотрим, как он сыграл со вторым и т. д. Если мы в конце концов найдем среди упорядоченных k участников такого, у которого (k + 1)-й выиграл (а предыдущему проиграл), то поставим (k + 1)-го перед ним, в противном случае поставим его на последнее место. В результате все k + 1 участника будут расположены в необходимом порядке.

Среди матчевых систем с математической точки зрения наиболее интересна схевенингенская, на которой мы сейчас и остановимся. В турнире по «схевенингену» встречаются две команды, и каждый участник одной из них играет с каждым участником другой. Таким образом, наряду с основным матчем удается провести также интересный личный турнир (и поэтому эта система, по существу, является матч-турнирной).

Рис. 73. Расписание игр схевенингенского турнира

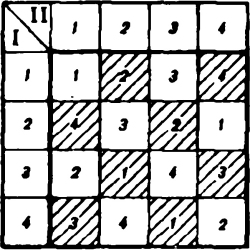
Пусть каждая команда состоит из n шахматистов. В этом случае схевенингенский турнир продрлжается ровно п туров. Для n = 6 возможное расписание турнирг представлено на рис. 73, причем оно легко обобщается для любого n. Здесь строки таблицы соответствуют участникам первой команды, а столбцы - участникам второй. Номер тура, г котором играют между собой данные противники, стоит в клетке, лежащей на пересечении соответствующей строки и столбца, а цвет фигур (участников первой команды) определяется цветом этой клетки.

Каждый столбец и каждая строка квадрата, выделенного на рис. 73, содержат все числа от 1 до 6, расположенные в том или ином порядке. В общем случае строки и столбцы квадрата содержат все числа от 1 до n. Такой квадрат в комбинаторном анализе называется латинским квадратом порядка п. (Эйлер, который исследовал эти квадраты, вместо чисел пользовался латинскими буквами, чем и объясняется название таких квадратов.) Ясно, что всякий латинский квадрат порядка n, клетки которого окрашены в черно-белый цвет, дает некоторое расписание схевенингенского турнира для двух команд, состоящих из n шахматистов.

В расписании на рис. 73 все шахматисты играют одинаковое число партий белыми и черными, что само но себе хорошо. В то же время обе команды здесь в каждом туре все партии играют одним цветом, и это нельзя признать удачным, так как команда, играющая белыми, имеет явное преимущество.

Организаторы товарищеского матча СССР - Югославия, состоявшегося в 1970 г., попытались найти расписание (для мужских команд, состоящих из шести человек каждая), удовлетворяющее сразу трем следующим, довольно естественным, условиям:

1) все шахматисты играют одинаковое число партий белыми и черными;

2) в каждом туре участники обеих команд играют одинаковое число партий белыми и черными;

3) все шахматисты в каждом туре меняют цвет фигур.

В общем случае задача состоит в нахождении тех значений n, при которых существует расписание «схевенингена», удовлетворяющее этим трем условиям.

Очевидно, следует рассматривать только четные n, так как в противном случае одновременно нарушаются первые два условия.

Если все участники команды в каждом туре играют одним цветом (как в расписании на рис. 73), то условие

3) выполняется, а условие 2) - нет. Однако условия 2) и 3) одновременно выполняться не могут. Действительно, если имеет место условие 2), то найдутся хотя бы два представителя разных команд, которые уже в первом туре играют одним цветом. Так как по условию 3) эти шахматисты в каждом туре должны менять цвет фигур, то они до конца турнира не встретятся между собой!

Будем считать условие 2) более важным и ради него откажемся от условия 3) (организаторы упомянутого матча именно так и поступили). Теперь надо выяснить, существует ли расписание схевенингенского турнира, удовлетворяющее только первым двум условиям. Перед началом матча СССР - Югославия организаторы попытались найти такое расписание, но у них ничего не вышло.

Предположим, что клетки некоторого латинского квадрата порядка n можно раскрасить в черный и белый цвета так, чтобы одновременно выполнялись следующие два условия;

а) в каждом столбце и в каждой строке квадрата содержится одинаковое число белых и черных клеток;

б) половина всех клеток квадрата, в которых записано одно и то же число (любое), окрашена в белый цвет, а половина - в черный.

Раскрашенный указанным образом латинский квадрат дает расписание «схевенингена», удовлетворяющее условиям 1) и 2) - для команд, состоящих из n шахматистов. Действительно, из а) непосредственно следует справедливость условия 1), а из б) - условия 2).

Итак, возникает следующая чисто математическая задача, эквивалентная нашей задаче о составлении расписания.

При каких n (четных) существует латинский квадрат порядка n, клетки которого можно раскрасить в черный и белый цвета так₉ чтобы одновременно выполнялись условия а) и б)?

Введем еще одно понятие, связанное с латинскими квадратами. При наложении одного такого квадрата на другой (оба порядка n) получаются n² пар чисел, стоящих на одинаковых местах - первое число пары берется из первого квадрата, а второе - из второго квадрата (пары, отличающиеся порядком чисел, считаются различными). Два латинских квадрата порядка n называются ортогональными, если все n² пар чисел, возникающих при наложении, отличаются друг от друга. Например, латинские квадраты четвертого порядка на рис. 74 ортогональны, так как при наложении одного из них н а другой все n² = 16 пар чисел различны.

Покажем, что если существуют два ортогональных латинских квадрата порядка n (n четно), то каждый из них можно раскрасить так, чтобы выполнялись условия а) и б).

Предположим, что указанные квадраты существуют. Возьмем в этом случае один из них в качестве исходного и закрасим в черный цвет все те его клетки, на которые при наложении второго квадрата попадают клетки с четными числами (остальные клетки первого квадрата - белые). Убедимся, что наш раскрашенный квадрат удовлетворяет условиям а) и б). Так как в каждой строке и в каждом столбце произвольного латинского квадрата половина чисел четна, а половина нечетна (при четном n), то при указанной раскраске условие а) выполняется. Ввиду ортогональности выбранных квадратов каждым n одинаковым числам исходного квадрата соответствует половина четных и половина нечетных чисел второго квадрата, т. е. условие б) также выполняется.

В качестве примера рассмотрим два ортогональных латинских квадрата четвертого порядка (рис. 74,а-б). При наложении второго из них на первый (рис. 74,в) и соответствующем раскрашивании клеток мы получаем расписание схевенингенского турнира для двух команд, состоящих из четырех шахматистов (рис. 74,г). Интересно, что клетки этой таблицы раскрашены в шахматном норядке.

Рис. 74. Ортогональные латинские квадраты четвертого порядка и соответствующее им расписание

Итак, задача о шахматном турнире неожиданно привела нас к одному из интереснейших разделов комбинаторного анализа - теории латинских квадратов! Проблема существования ортогональных латинских квадратов в общем случае не поддавалась разгадке около 200 лет. Лишь в 1960 г. было, наконец, доказано, что ортогональные квадраты существуют для всех n, не равных 2 и 6. Из этого результата вытекает, в частности, что не имеет решения известная задача Эйлера о 36 офицерах: в клетках квадрата 6×6 разместить делегации от 6 полков, состоящие из шести офицеров разного звания, так, чтобы ни в одном горизонтальном и вертикальном ряду не повторялись ни полк, ни звание. Действительно, эта задача эквивалентна задаче нахождения пары ортогональных квадратов шестого порядка, а такой пары не существует.

Теперь мы знаем, что для любой пары команд, состоящих из четного числа шахматистов (но не из двух и не из шести!) существует расписание схевенингенского турнира, удовлетворяющее условиям 1 и 2. Однако в упомянутом матче СССР - Югославия каждую страну (на мужских досках) представляло именно шесть человек, и поэтому наша проблема снова остается открытой. В самом деле, при n = 2 или n = 6 мы не можем утверждать, что расписание имеется, хотя и нет оснований утверждать обратное (во всяком случае, из отсутствия ортогональных квадратов это не следует).

Рис. 75. Идеальное расписание схевенингенского турнира, составленное ЭВМ

Простой перебор показывает, что для n = 2 нужное расписание составить невозможно. Что же касается интересующего нас случая n = 6, то здесь ручной перебор вариантов чрезвычайно велик. Чтобы «закрыть» проблему, математик и шахматный мастер А. Битман решил прибегнуть к помощи ЭВМ. Предварительно из всех латинских квадратов шестого порядка он отобрал лишь 22 так называемых неизоморфных (остальные получаются из них перестановкой строк и столбцов и ничего нового не дают). Машине предстояло «раскрасить» эти 22 квадрата всевозможными способами и выяснить, существуют ли раскраски, удовлетворяющие условиям а) и б).

В результате в 16 случаях из 22 ЭВМ обнаружила необходимую раскраску. Таким образом, искомое расписание схевенингенского турнира было найдено! Одно из них показано на рис. 75 (в отличие от рис. 74,г в данном случае раскраска не является шахматной). Это расписание примечательно еще и тем, что здесь никто из шахматистов не играет более двух партий подряд одним цветом. Поскольку полного чередования цвета, как мы знаем, добиться невозможно, то расписание на рис. 75 можно считать идеальным.

54. От названия голландского города Схевенинген; в шахматной литературе эту систему часто (хотя и не точно) называют шевенингенской, или, кратко, шевенинген.

55. Исчерпывающее решение ряда таких задач приведено в журнале «Квант», 1972, № 8.